5. 如图,水坝的横截面为梯形 $ ABCD $,迎水坡 $ AD $ 的坡角为 $ 30^{\circ} $,背水坡 $ BC $ 的坡度为 $ 1 : 1 $,坝顶宽 $ AB $ 为 $ 4 \, \mathrm{m} $,坝高为 $ 6 \, \mathrm{m} $.
(1) 求坝底宽 $ CD $;
(2) 若不改变水坝的坡度和坝底宽 $ CD $,而要用土将这段长度为 $ 1000 \, \mathrm{m} $ 的堤坝加高 $ 0.5 \, \mathrm{m} $,问需要多少土方(精确到 $ 1 \, \mathrm{m}^3 $)?

(1) 求坝底宽 $ CD $;
(2) 若不改变水坝的坡度和坝底宽 $ CD $,而要用土将这段长度为 $ 1000 \, \mathrm{m} $ 的堤坝加高 $ 0.5 \, \mathrm{m} $,问需要多少土方(精确到 $ 1 \, \mathrm{m}^3 $)?

答案:
解: (1)过点A作AE⊥CD,垂足为点E,过点B作BF⊥CD,垂足为点F
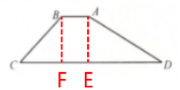
由题意可知,四边形AEFB是矩形,AB=EF=4m,BF=AE=6m,∠D=30°
在Rt△ADE中,∵∠D=30°,AE=6m
∴$DE=\sqrt 3AE= 6\sqrt 3\ \mathrm {m}$
在Rt△CBF 中,∵背水坡BC的坡度为1 : 1,即BF:CF=1: 1
∴CF=BF=6m
∴$CD=CF+EF+DE=(10 + 6\sqrt 3)\ \mathrm {m}$
(2)增加的部分为梯形。梯形的面积:$\frac {(4- 0.5- 0.5\sqrt 3 + 4)}2×0.5×1000≈1658\ \mathrm {m^2}$
∴需要$1658\ \mathrm {m^3}$的土方。
解: (1)过点A作AE⊥CD,垂足为点E,过点B作BF⊥CD,垂足为点F

由题意可知,四边形AEFB是矩形,AB=EF=4m,BF=AE=6m,∠D=30°
在Rt△ADE中,∵∠D=30°,AE=6m
∴$DE=\sqrt 3AE= 6\sqrt 3\ \mathrm {m}$
在Rt△CBF 中,∵背水坡BC的坡度为1 : 1,即BF:CF=1: 1
∴CF=BF=6m
∴$CD=CF+EF+DE=(10 + 6\sqrt 3)\ \mathrm {m}$
(2)增加的部分为梯形。梯形的面积:$\frac {(4- 0.5- 0.5\sqrt 3 + 4)}2×0.5×1000≈1658\ \mathrm {m^2}$
∴需要$1658\ \mathrm {m^3}$的土方。
6. 如图,一个热气球从小山东侧点 $ A $ 处开始升空,由于受西风的影响,热气球以 $ 30 \, \mathrm{m/min} $ 的速度沿与地面成 $ 75^{\circ} $ 角的方向飞行,$ 25 \, \mathrm{min} $ 后到达 $ C $ 处,此时从热气球上观测小山西侧点 $ B $ 的俯角 $ \angle DCB $ 为 $ 30^{\circ} $,则小山两侧的点 $ A $、$ B $ 间的距离为

750√2
$ \mathrm{m} $.
答案:$750 \sqrt{2}$
7. 如图是某水库的截面示意图,其中 $ AB $、$ CD $ 分别表示水库上、下游的水面,$ \angle ABC = 120^{\circ} $,$ BC = 50 \, \mathrm{m} $,则水库上、下游水面的高度差 $ h $ 为(

A.$ 25\sqrt{3} \, \mathrm{m} $
B.$ 25 \, \mathrm{m} $
C.$ 25\sqrt{2} \, \mathrm{m} $
D.$ \dfrac{50\sqrt{3}}{3} \, \mathrm{m} $
A
).
A.$ 25\sqrt{3} \, \mathrm{m} $
B.$ 25 \, \mathrm{m} $
C.$ 25\sqrt{2} \, \mathrm{m} $
D.$ \dfrac{50\sqrt{3}}{3} \, \mathrm{m} $
答案:A
8. 如图,梯形 $ ABCD $ 是拦水坝的横截面图,坡面 $ CD $ 的坡度是 $ 1 : \sqrt{3} $,$ \angle B = 60^{\circ} $,$ AB = 6 \, \mathrm{m} $,$ AD = 4 \, \mathrm{m} $. 求拦水坝的横截面 $ ABCD $ 的面积(精确到 $ 0.1 \, \mathrm{m}^2 $).


答案:
解:过点A作AE⊥BC,垂足为E,过点D作DF⊥BC,垂足为F
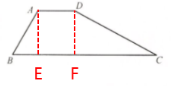
在Rt△ABE中,∵∠B=60°,AB=6m
∴BE= AB · cos 60°= 3m,$AE= AB · sin 60°= 3\sqrt 3m$
∵四边形ABCD是梯形
∴AD//EF
∵AE⊥BC,DF⊥BC
∴∠AEF=∠DFE=∠ EAD= 90°
∴四边形AEFD是矩形
∴EF=AD=4m,$DF=AE=3\sqrt 3m$
在Rt△CDF 中,坡面CD的坡度是1:$\sqrt 3$
∴$CF=\sqrt 3DF = 9m$
∴BC=BE+EF+CF=16m
∴$S_{梯形ABCD}= \frac {1}{2}(AD+ BC)×AE= 30\sqrt 3≈52.0\ \mathrm {m^2}$
答:横截面ABCD的面积为$52.0\ \mathrm {m^2}。$
解:过点A作AE⊥BC,垂足为E,过点D作DF⊥BC,垂足为F

在Rt△ABE中,∵∠B=60°,AB=6m
∴BE= AB · cos 60°= 3m,$AE= AB · sin 60°= 3\sqrt 3m$
∵四边形ABCD是梯形
∴AD//EF
∵AE⊥BC,DF⊥BC
∴∠AEF=∠DFE=∠ EAD= 90°
∴四边形AEFD是矩形
∴EF=AD=4m,$DF=AE=3\sqrt 3m$
在Rt△CDF 中,坡面CD的坡度是1:$\sqrt 3$
∴$CF=\sqrt 3DF = 9m$
∴BC=BE+EF+CF=16m
∴$S_{梯形ABCD}= \frac {1}{2}(AD+ BC)×AE= 30\sqrt 3≈52.0\ \mathrm {m^2}$
答:横截面ABCD的面积为$52.0\ \mathrm {m^2}。$