7. 如图,一艘船以 $ 30 $ n mile/h 的速度向北偏东 $ 45^{\circ} $ 方向航行,在 $ A $ 处时观测灯塔 $ S $ 在北偏东 $ 75^{\circ} $ 的方向,航行 $ 12 $ min 后到达 $ B $ 处时再观测灯塔 $ S $ 恰好在正东方向. 已知距离此灯塔 $ 8 $ n mile 以外的海区为航行安全区域,这艘船可以继续沿北偏东 $ 45^{\circ} $ 方向航行吗?为什么?


答案:
解:可以,理由如下:
过点S 作AB的垂线,交AB的延长线于点C

由题意可知,∠CAS=75°-45°=30°,∠CBS=45°
设CS= x海里
在Rt△ACS 中,∵∠CAS=30°,CS=x,$AC=\sqrt 3CS=\sqrt 3x$
在Rt△BCS 中,∵∠CBS=45°,CS=x
∴BC= CS=x
∵$AB= \frac {12}{60}× 30= 6$海里
∴$\sqrt 3x-x=6$
解得,$x= 3\sqrt 3+3≈8.2$
∵点S 到直线AB的距离CS=8.2海里$\gt 8$海里
∴这艘船可以继续沿北偏东45°方向航行
解:可以,理由如下:
过点S 作AB的垂线,交AB的延长线于点C
由题意可知,∠CAS=75°-45°=30°,∠CBS=45°
设CS= x海里
在Rt△ACS 中,∵∠CAS=30°,CS=x,$AC=\sqrt 3CS=\sqrt 3x$
在Rt△BCS 中,∵∠CBS=45°,CS=x
∴BC= CS=x
∵$AB= \frac {12}{60}× 30= 6$海里
∴$\sqrt 3x-x=6$
解得,$x= 3\sqrt 3+3≈8.2$
∵点S 到直线AB的距离CS=8.2海里$\gt 8$海里
∴这艘船可以继续沿北偏东45°方向航行
8. 如图,某海岛附近海域有两艘自西向东航行的船 $ A $、$ B $,船 $ B $ 在船 $ A $ 的正东方向,且两船保持 $ 20 $ n mile 的距离,某一时刻两船同时测得在船 $ A $ 的东北方向、船 $ B $ 的北偏东 $ 15^{\circ} $ 方向有一艘船 $ C $. 求此时船 $ C $ 与船 $ B $ 的距离(保留根号).


答案:
解:过点B作BD ⊥AC,垂足为D
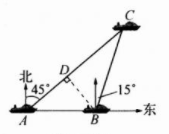
由题意,可知∠BAC=45°,∠ABC=90°+15°=105°
∴∠ACB=180°-∠BAC-∠ABC=30°
在Rt△ABD中,$BD=AB · s in ∠BAD=20× \frac {\sqrt 2}2=10 \sqrt{2} ($海里)
在 Rt△BCD中,$BC=\frac {BD}{sin∠BCD}= \frac {10\sqrt{2}}{\frac {1}{2}}=20 \sqrt{2} ($海里)
∴此时船C与船B的距离是$20 \sqrt{2} $海里
解:过点B作BD ⊥AC,垂足为D

由题意,可知∠BAC=45°,∠ABC=90°+15°=105°
∴∠ACB=180°-∠BAC-∠ABC=30°
在Rt△ABD中,$BD=AB · s in ∠BAD=20× \frac {\sqrt 2}2=10 \sqrt{2} ($海里)
在 Rt△BCD中,$BC=\frac {BD}{sin∠BCD}= \frac {10\sqrt{2}}{\frac {1}{2}}=20 \sqrt{2} ($海里)
∴此时船C与船B的距离是$20 \sqrt{2} $海里
9. 如图,要在宽 $ 22 $ m 的九洲大道 $ AB $ 两边安装路灯,路灯的灯臂 $ CD $ 的长为 $ 2 $ m,且与灯柱 $ BC $ 成 $ 120^{\circ} $ 角,路灯采用圆锥形灯罩,灯罩的中轴线 $ DO $ 与灯臂 $ CD $ 垂直,当灯罩的中轴线 $ DO $ 通过公路路面的中心线时照明效果最佳. 此时,路灯的灯柱 $ BC $ 的高度应为多少米(保留根号)?


答案:
解:过点D作DE⊥AB,垂足为E,过点C作CF⊥DE,垂足为F
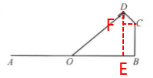
∵∠DCB=120°,CB⊥AB,OD⊥CD
∴∠DOB=360°-∠DCB-∠CBO-∠ODC=360°-120°-90°-90°=60°,即∠DCF=30°
∴$CF=CD · cos_{30}°=2× \frac {\sqrt{3}}{2}=\sqrt 3,$$DF=\frac {1}{2}\ \mathrm {CD}=1$
∴$CF=BE=\sqrt{3} $
∴$OE=OB-BE=\frac {1}{2}\ \mathrm {AB}-BE=11-\sqrt{3} $
∴$DE= tan 60° · OE =\sqrt{3} (11- \sqrt{3} )=11 \sqrt{3} -3$
∴$BC=DE-DF=11 \sqrt{3} -3-1=11 \sqrt{3} -4$
解:过点D作DE⊥AB,垂足为E,过点C作CF⊥DE,垂足为F

∵∠DCB=120°,CB⊥AB,OD⊥CD
∴∠DOB=360°-∠DCB-∠CBO-∠ODC=360°-120°-90°-90°=60°,即∠DCF=30°
∴$CF=CD · cos_{30}°=2× \frac {\sqrt{3}}{2}=\sqrt 3,$$DF=\frac {1}{2}\ \mathrm {CD}=1$
∴$CF=BE=\sqrt{3} $
∴$OE=OB-BE=\frac {1}{2}\ \mathrm {AB}-BE=11-\sqrt{3} $
∴$DE= tan 60° · OE =\sqrt{3} (11- \sqrt{3} )=11 \sqrt{3} -3$
∴$BC=DE-DF=11 \sqrt{3} -3-1=11 \sqrt{3} -4$