4. 小明和小强一起到郊外放风筝,他们把风筝放飞后,将两个风筝的引线一端都固定在地面上的点 $ C $ 处(如图). 若此时风筝线 $ AC = 20 $ m,$ BC = 24 $ m,在 $ C $ 处观测风筝 $ A $、$ B $ 的仰角分别为 $ 60^{\circ} $ 和 $ 45^{\circ} $.
(1)试通过计算,比较风筝 $ A $ 与风筝 $ B $ 哪一个离地面更高;
(2)求风筝 $ A $ 与风筝 $ B $ 的水平距离(精确到 $ 0.01 $ m. 参考数据:$ \sin 45^{\circ} \approx 0.707 $,$ \cos 45^{\circ} \approx 0.707 $,$ \tan 45^{\circ} = 1 $,$ \sin 60^{\circ} \approx 0.866 $,$ \cos 60^{\circ} = 0.5 $,$ \tan 60^{\circ} \approx 1.732 $).

(1)试通过计算,比较风筝 $ A $ 与风筝 $ B $ 哪一个离地面更高;
(2)求风筝 $ A $ 与风筝 $ B $ 的水平距离(精确到 $ 0.01 $ m. 参考数据:$ \sin 45^{\circ} \approx 0.707 $,$ \cos 45^{\circ} \approx 0.707 $,$ \tan 45^{\circ} = 1 $,$ \sin 60^{\circ} \approx 0.866 $,$ \cos 60^{\circ} = 0.5 $,$ \tan 60^{\circ} \approx 1.732 $).

答案:解:(1)分别过点A、B作地面的垂线,垂足分别为D、E
在Rt△ADC中,∵AC=20,∠ACD=60°
∴$AD=20×s in 60°=10\sqrt 3≈17.32\ \mathrm {m}$
在 Rt △BEC中,∵BC=24,∠BCE=45°
∴$BE=24× s in 45°=12 \sqrt{2} ≈16.97\ \mathrm {m}$
∵$17.32\gt 16.97$
∴风筝A比风筝B离地面更高
(2) 在Rt△ADC中,∵AC=20,∠ACD=60°
∴$DC=20× cos 60°=10\ \mathrm {m}$
在 Rt △BEC中,∵BC=24,∠BCE=45°
∴$EC=BC≈ 16.97\ \mathrm {m}$
∴$EC-DC=6.97\ \mathrm {m},$即风筝A与风筝B的水平距离约为$6.97\ \mathrm {m}$
在Rt△ADC中,∵AC=20,∠ACD=60°
∴$AD=20×s in 60°=10\sqrt 3≈17.32\ \mathrm {m}$
在 Rt △BEC中,∵BC=24,∠BCE=45°
∴$BE=24× s in 45°=12 \sqrt{2} ≈16.97\ \mathrm {m}$
∵$17.32\gt 16.97$
∴风筝A比风筝B离地面更高
(2) 在Rt△ADC中,∵AC=20,∠ACD=60°
∴$DC=20× cos 60°=10\ \mathrm {m}$
在 Rt △BEC中,∵BC=24,∠BCE=45°
∴$EC=BC≈ 16.97\ \mathrm {m}$
∴$EC-DC=6.97\ \mathrm {m},$即风筝A与风筝B的水平距离约为$6.97\ \mathrm {m}$
5. 如图,一艘轮船由海面 $ A $ 地出发沿南偏西 $ 40^{\circ} $ 的方向行驶 $ 40 $ n mile($ 1 $ n mile $ = 1852 $ m)到达 $ B $ 地,再由 $ B $ 地沿北偏西 $ 20^{\circ} $ 的方向行驶 $ 40 $ n mile 到达 $ C $ 地,则 $ A $、$ C $ 两地相距(

A.$ 30 $ n mile
B.$ 40 $ n mile
C.$ 50 $ n mile
D.$ 60 $ n mile
B
).
A.$ 30 $ n mile
B.$ 40 $ n mile
C.$ 50 $ n mile
D.$ 60 $ n mile
答案:B
6. 如图,在一条东西方向的航线 $ l $ 的两侧分别有观测点 $ A $ 和 $ B $,点 $ A $ 到航线 $ l $ 的距离为 $ 2 $ km,点 $ B $ 位于点 $ A $ 北偏东 $ 60^{\circ} $ 方向且与 $ A $ 相距 $ 10 $ km 处. 现有一艘轮船从位于点 $ B $ 南偏西 $ 76^{\circ} $ 方向的 $ C $ 处,正沿该航线自西向东航行,$ 5 $ min 后该轮船行至点 $ A $ 正北方向的 $ D $ 处.
(1)求观测点 $ B $ 到航线 $ l $ 的距离;
(2)求该轮船航行的速度(精确到 $ 0.1 $ km/h. 参考数据:$ \sqrt{3} \approx 1.73 $,$ \sin 76^{\circ} \approx 0.97 $,$ \cos 76^{\circ} \approx 0.24 $,$ \tan 76^{\circ} \approx 4.01 $).

(1)求观测点 $ B $ 到航线 $ l $ 的距离;
(2)求该轮船航行的速度(精确到 $ 0.1 $ km/h. 参考数据:$ \sqrt{3} \approx 1.73 $,$ \sin 76^{\circ} \approx 0.97 $,$ \cos 76^{\circ} \approx 0.24 $,$ \tan 76^{\circ} \approx 4.01 $).

答案:
解: (1)过点B作AD的垂线,交AD的延长线于点E
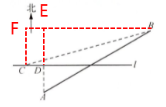
由题意可知,$AD=2\ \mathrm {km},$$AB=10\ \mathrm {km},$∠BAE=60°,∠BCF=76°
在Rt△ABE中,∵∠BAE=60°,$AB=10\ \mathrm {km}$
∴$AE=AB×cos 60° =5\ \mathrm {km},$$BE=AB×sin 60°=5\sqrt 3\ \mathrm {km}$
∵$AD= 2\ \mathrm {km}$
∴$DE= 3\ \mathrm {km}$
答:观测点B到航线l的距离为$3\ \mathrm {km}。$
(2)过点C作BE的垂线,与BE的延长线交于点F
在Rt△BCF 中,∵∠BCF=76°,$CF=DE=3\ \mathrm {km}$
∴$BF=CF×tan_{76}°≈12.03\ \mathrm {km}$
∵$BE=5\sqrt 3≈8.65\ \mathrm {km}$
∴$EF= BF-BE=3.38\ \mathrm {km}$
∴航行的速度为$3.38 × 12≈40.6\ \mathrm {km/h}$
答:该轮船航行的速度为$40.6\ \mathrm {km/h}。$
解: (1)过点B作AD的垂线,交AD的延长线于点E

由题意可知,$AD=2\ \mathrm {km},$$AB=10\ \mathrm {km},$∠BAE=60°,∠BCF=76°
在Rt△ABE中,∵∠BAE=60°,$AB=10\ \mathrm {km}$
∴$AE=AB×cos 60° =5\ \mathrm {km},$$BE=AB×sin 60°=5\sqrt 3\ \mathrm {km}$
∵$AD= 2\ \mathrm {km}$
∴$DE= 3\ \mathrm {km}$
答:观测点B到航线l的距离为$3\ \mathrm {km}。$
(2)过点C作BE的垂线,与BE的延长线交于点F
在Rt△BCF 中,∵∠BCF=76°,$CF=DE=3\ \mathrm {km}$
∴$BF=CF×tan_{76}°≈12.03\ \mathrm {km}$
∵$BE=5\sqrt 3≈8.65\ \mathrm {km}$
∴$EF= BF-BE=3.38\ \mathrm {km}$
∴航行的速度为$3.38 × 12≈40.6\ \mathrm {km/h}$
答:该轮船航行的速度为$40.6\ \mathrm {km/h}。$