25. 如图,在五边形 $ABCDE$ 中,$AP$ 平分 $\angle EAB$,且 $AP// DE$,交 $CD$ 于点 $P$.
(1)五边形 $ABCDE$ 的内角和为
(2)若 $\angle C = 100^{\circ}$,$\angle D = 75^{\circ}$,$\angle E = 135^{\circ}$,求 $\angle B$ 的度数.
 ]
]
(1)五边形 $ABCDE$ 的内角和为
$540 ^ { \circ }$
;(2)若 $\angle C = 100^{\circ}$,$\angle D = 75^{\circ}$,$\angle E = 135^{\circ}$,求 $\angle B$ 的度数.
 ]
]答案:25.(1)$540 ^ { \circ }$ (2)$\because AP// DE$,$\angle E=135°$,$\therefore \angle EAP=180°-\angle E=45°$。$\because AP$平分$\angle EAB$,$\therefore \angle EAB=2\angle EAP=90°$。$\because \angle C=100°$,$\angle D=75°$,$\therefore \angle B=540°-\angle C-\angle EAB-\angle E-\angle D=140°$
解析:
(1) $540°$
(2) 解:$\because AP // DE$,$\angle E = 135°$,
$\therefore \angle EAP = 180° - \angle E = 180° - 135° = 45°$。
$\because AP$平分$\angle EAB$,
$\therefore \angle EAB = 2\angle EAP = 2 × 45° = 90°$。
$\because$五边形内角和为$540°$,$\angle C = 100°$,$\angle D = 75°$,
$\therefore \angle B = 540° - \angle EAB - \angle E - \angle D - \angle C = 540° - 90° - 135° - 75° - 100° = 140°$。
(2) 解:$\because AP // DE$,$\angle E = 135°$,
$\therefore \angle EAP = 180° - \angle E = 180° - 135° = 45°$。
$\because AP$平分$\angle EAB$,
$\therefore \angle EAB = 2\angle EAP = 2 × 45° = 90°$。
$\because$五边形内角和为$540°$,$\angle C = 100°$,$\angle D = 75°$,
$\therefore \angle B = 540° - \angle EAB - \angle E - \angle D - \angle C = 540° - 90° - 135° - 75° - 100° = 140°$。
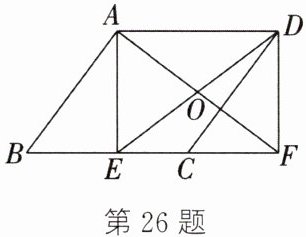
26. 如图,在 $□ ABCD$ 中,$AE⊥ BC$ 于点 $E$,延长 $BC$ 至点 $F$,使 $CF = BE$,连接 $DF$,$AF$ 与 $DE$ 交于点 $O$.
(1)求证:四边形 $AEFD$ 为矩形;
(2)若 $AB = 6$,$OE = 4$,$\angle BAE = \angle DEF$,求 $BF$,$DF$ 的长.
(1)求证:四边形 $AEFD$ 为矩形;
(2)若 $AB = 6$,$OE = 4$,$\angle BAE = \angle DEF$,求 $BF$,$DF$ 的长.

答案:26.(1)$\because BE=CF$,$\therefore BE+CE=CF+CE$,即$BC=EF$。$\because$四边形ABCD是平行四边形,$\therefore AD// BC$,$AD=BC$。$\therefore AD=BC=EF$。又$\because AD// EF$,$\therefore$四边形AEFD为平行四边形。$\because AE⊥ BC$,$\therefore \angle AEF=90°$。$\therefore$四边形AEFD为矩形
(2)$\because$四边形AEFD为矩形,$\therefore AF=DE$,$OA=OF=\frac{1}{2}AF$,$OD=OE=\frac{1}{2}DE$,$AE=DF$。$\therefore AF=DE=2OE=8$,$OA=OF=OD=OE$。$\therefore \angle DEF=\angle AFE$。又$\because \angle AEF=90°$,$\therefore \angle EAF+\angle AFE=90°$。$\because \angle BAE=\angle DEF$,$\therefore \angle BAE+\angle EAF=90°$,即$\angle BAF=90°$。在$Rt\triangle BAF$中,由勾股定理,得$BF=\sqrt{AB^{2}+AF^{2}}=\sqrt{6^{2}+8^{2}}=10$。$\because S_{\triangle BAF}=\frac{1}{2}AB· AF=\frac{1}{2}BF· AE$,$\therefore \frac{1}{2}×6×8=\frac{1}{2}×10× AE$。$\therefore AE=4.8$。$\therefore DF=AE=4.8$
(2)$\because$四边形AEFD为矩形,$\therefore AF=DE$,$OA=OF=\frac{1}{2}AF$,$OD=OE=\frac{1}{2}DE$,$AE=DF$。$\therefore AF=DE=2OE=8$,$OA=OF=OD=OE$。$\therefore \angle DEF=\angle AFE$。又$\because \angle AEF=90°$,$\therefore \angle EAF+\angle AFE=90°$。$\because \angle BAE=\angle DEF$,$\therefore \angle BAE+\angle EAF=90°$,即$\angle BAF=90°$。在$Rt\triangle BAF$中,由勾股定理,得$BF=\sqrt{AB^{2}+AF^{2}}=\sqrt{6^{2}+8^{2}}=10$。$\because S_{\triangle BAF}=\frac{1}{2}AB· AF=\frac{1}{2}BF· AE$,$\therefore \frac{1}{2}×6×8=\frac{1}{2}×10× AE$。$\therefore AE=4.8$。$\therefore DF=AE=4.8$
27. (2025·海门期中)在正方形 $ABCD$ 中,$G$ 是射线 $AC$ 上一动点(不与点 $A$,$C$ 重合),连接 $BG$,作 $BH⊥ BG$,且使 $BH = BG$,连接 $GH$,$CH$.
(1)如图①,若点 $G$ 在线段 $AC$ 上.
① 图中与 $\triangle ABG$ 全等的三角形是
② 线段 $AG$,$CG$,$GH$ 之间的数量关系是
(2)如图②,若点 $G$ 在 $AC$ 的延长线上,则线段 $AG$,$CG$,$BG$ 之间有怎样的数量关系?写出结论,并给出证明.
 ]
]
(1)如图①,若点 $G$ 在线段 $AC$ 上.
① 图中与 $\triangle ABG$ 全等的三角形是
$\triangle CBH$
;② 线段 $AG$,$CG$,$GH$ 之间的数量关系是
$AG^{2}+CG^{2}=GH^{2}$
。(2)如图②,若点 $G$ 在 $AC$ 的延长线上,则线段 $AG$,$CG$,$BG$ 之间有怎样的数量关系?写出结论,并给出证明.
 ]
]答案:27.(1)①$\triangle CBH$ ②$AG^{2}+CG^{2}=GH^{2}$ (2)$AG^{2}+CG^{2}=2BG^{2}$ $\because$四边形ABCD是正方形,$\therefore \angle ABC=90°$,$\angle BAC=\angle BCA=45°$,$AB=BC$。$\because \angle GBH=90°$,$\therefore \angle ABC+\angle GBC=\angle GBH+\angle GBC$,即$\angle ABG=\angle CBH$。又$\because BG=BH$,$\therefore \triangle ABG\cong\triangle CBH$。$\therefore AG=CH$,$\angle BAG=\angle BCH=45°$。$\therefore \angle ACH=\angle ACB+\angle BCH=45°+45°=90°$。$\therefore \angle GCH=180°-\angle ACH=90°$。在$Rt\triangle GCH$中,由勾股定理,得$CH^{2}+CG^{2}=GH^{2}$,$\therefore AG^{2}+CG^{2}=GH^{2}$。$\because \angle GBH=90°$,$BG=BH$,$\therefore GH^{2}=BG^{2}+BH^{2}=2BG^{2}$。$\therefore AG^{2}+CG^{2}=2BG^{2}$