1. 六年级一班的男生人数是女生人数的$\frac{4}{5}$,女生和男生的人数比是(
5 : 4
),男生人数占全班人数的$\frac{(\space)}{(\space)}$,女生人数比男生人数多(25
)%。答案:1. 5 : 4 $\frac{4}{9}$ 25
2. 在一道减法算式中,被减数是 300,差是减数的$\frac{2}{3}$,减数是(
180
),差是(120
)。答案:2. 180 120
解析:
设减数为$x$,则差为$\frac{2}{3}x$。
因为被减数 - 减数 = 差,所以$300 - x = \frac{2}{3}x$
$300 = x + \frac{2}{3}x$
$300 = \frac{5}{3}x$
$x = 300 ÷ \frac{5}{3}$
$x = 300 × \frac{3}{5}$
$x = 180$
差为$\frac{2}{3}x = \frac{2}{3} × 180 = 120$
180 120
因为被减数 - 减数 = 差,所以$300 - x = \frac{2}{3}x$
$300 = x + \frac{2}{3}x$
$300 = \frac{5}{3}x$
$x = 300 ÷ \frac{5}{3}$
$x = 300 × \frac{3}{5}$
$x = 180$
差为$\frac{2}{3}x = \frac{2}{3} × 180 = 120$
180 120
3. (2025·扬州江都区期末)近期“苏超”联赛掀起足球热,学校打算为五、六年级共22个班级添置足球,五年级每个班2个足球,六年级每个班3个足球,一共要买54个足球。该校五年级有(
12
)个班,六年级有(10
)个班。答案:3. 12 10
解析:
设五年级有$x$个班,则六年级有$(22 - x)$个班。
$2x + 3(22 - x) = 54$
$2x + 66 - 3x = 54$
$-x = 54 - 66$
$-x = -12$
$x = 12$
六年级班级数:$22 - 12 = 10$
12;10
$2x + 3(22 - x) = 54$
$2x + 66 - 3x = 54$
$-x = 54 - 66$
$-x = -12$
$x = 12$
六年级班级数:$22 - 12 = 10$
12;10
4. 天宫举行宴会,宴请各路神仙和天兵。神仙和天兵一共来了120人,如果每个神仙喝5壶酒,每5个天兵喝1壶酒,那么正好喝了120壶酒。神仙来了(
20
)人。答案:4. 20
解析:
设神仙来了$x$人,则天兵来了$(120 - x)$人。
每个神仙喝$5$壶酒,神仙共喝酒$5x$壶;每$5$个天兵喝$1$壶酒,天兵共喝酒$\frac{120 - x}{5}$壶。
根据题意可列方程:$5x+\frac{120 - x}{5}=120$
方程两边同时乘以$5$得:$25x + 120 - x=600$
合并同类项得:$24x=480$
解得:$x = 20$
20
每个神仙喝$5$壶酒,神仙共喝酒$5x$壶;每$5$个天兵喝$1$壶酒,天兵共喝酒$\frac{120 - x}{5}$壶。
根据题意可列方程:$5x+\frac{120 - x}{5}=120$
方程两边同时乘以$5$得:$25x + 120 - x=600$
合并同类项得:$24x=480$
解得:$x = 20$
20
5. 选一选。
(1)水结成冰,体积增加$\frac{1}{10}$;冰化成水,体积减少(
A. $\frac{1}{9}$
B. $\frac{1}{10}$
C. $\frac{1}{11}$
D. $\frac{1}{5}$
(2)红红家种了几种果树,其中桃树的棵数和其他果树棵数的比是$1:13$,梨树的棵数是其他果树棵数的5倍。若红红家种的果树总棵数在40和50之间,则红红家一共种了(
A. 40
B. 49
C. 42
D. 48
(1)水结成冰,体积增加$\frac{1}{10}$;冰化成水,体积减少(
C
)。A. $\frac{1}{9}$
B. $\frac{1}{10}$
C. $\frac{1}{11}$
D. $\frac{1}{5}$
(2)红红家种了几种果树,其中桃树的棵数和其他果树棵数的比是$1:13$,梨树的棵数是其他果树棵数的5倍。若红红家种的果树总棵数在40和50之间,则红红家一共种了(
C
)棵果树。A. 40
B. 49
C. 42
D. 48
答案:5. (1) C (2) C
6. 小明用A、B两种积木交替而且没有规律地拼成了一个大的长方体(如图),已知大长方体的长是36厘米,一共用了10块积木。A积木用了(
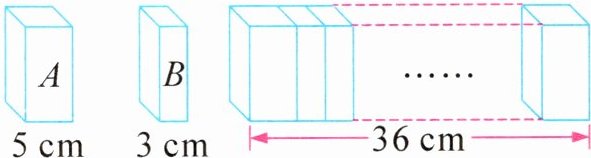
3
)块,B积木用了(7
)块。
答案:6. 3 7
7. 小枫在“红领巾小银行”储蓄的钱数是小寒的$\frac{2}{3}$,后来小枫又存进去4元,而小寒取走6元,此时小枫在“红领巾小银行”储蓄的钱数是小寒的$\frac{3}{4}$。现在小寒、小枫各储蓄多少元?
答案:7. 小寒$:(6 × \frac{2}{3} + 4) ÷ (\frac{3}{4} - \frac{2}{3}) = 96($元)
小枫$:96 × \frac{3}{4} = 72($元)
小枫$:96 × \frac{3}{4} = 72($元)
8. 一位出租车司机今天收到5元、10元、20元的人民币共44张,合计500元,其中10元与20元的张数相等。10元的人民币有(
14
)张。答案:8. 14 解析 10元和20元的张数相等,(20 + 10) ÷ 2 = 15(元),可以把每张10元或20元看成每张15元。假设全是5元的,一共是5 × 44 = 220(元),比实际少了500 - 220 = 280(元),这是因为5元的比15元的每张少10元,再用少的总钱数除以10,就是15元的张数,也就是10元和20元的总张数,再除以2即可求出10元有多少张。那么15元的张数就是280 ÷ 10 = 28(张),10元的张数即为28 ÷ 2 = 14(张)。
解析:
因为10元与20元的张数相等,所以将1张10元和1张20元看作一组,每组的钱数为$10 + 20 = 30$元,平均每张为$30÷2 = 15$元。
假设44张全是5元的,则总钱数为$5×44 = 220$元。
实际总钱数为500元,比假设的多$500 - 220 = 280$元。
每把1张5元换成1张15元,钱数会增加$15 - 5 = 10$元,所以15元的张数为$280÷10 = 28$张。
因为15元的张数是10元和20元的总张数,且10元和20元张数相等,所以10元的张数为$28÷2 = 14$张。
14
假设44张全是5元的,则总钱数为$5×44 = 220$元。
实际总钱数为500元,比假设的多$500 - 220 = 280$元。
每把1张5元换成1张15元,钱数会增加$15 - 5 = 10$元,所以15元的张数为$280÷10 = 28$张。
因为15元的张数是10元和20元的总张数,且10元和20元张数相等,所以10元的张数为$28÷2 = 14$张。
14
9. 亮点原创·师徒两人共加工零件105个,已知师傅加工零件个数的$\frac{3}{8}$与徒弟加工零件个数的$\frac{4}{7}$的和为49个,师徒两人各加工零件多少个?
答案:9. 师傅$:105 × \frac{4}{7} - 49 = 11($个$) 11 ÷ (\frac{4}{7} - \frac{3}{8}) = 56($个) 徒弟:105 - 56 = 49(个)
解析:
师傅:$105×\frac{4}{7}-49=11$(个)
$11÷(\frac{4}{7}-\frac{3}{8})=56$(个)
徒弟:$105 - 56 = 49$(个)
$11÷(\frac{4}{7}-\frac{3}{8})=56$(个)
徒弟:$105 - 56 = 49$(个)