例 1
如图,$\triangle ABC$ 的面积是 $24$ 平方厘米,已知 $BD = 2DA$,$BC = 4BE$,$DF:FC = 3:2$,那么 $\triangle DEF$ 的面积是多少平方厘米?
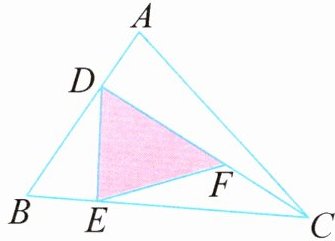
我的思考
由题意可知,线段之间存在着倍数关系,把线段之间的倍数关系转化为比的关系,通过线段之间比的关系求出线段所在的等高三角形的面积之比,结合已知的 $\triangle ABC$ 的面积,求出 $\triangle DEF$ 的面积。
我的解答
我的发现
我发现解决比和三角形相结合的题目时,先找出等高三角形:底边在同一条直线上,(
如图,$\triangle ABC$ 的面积是 $24$ 平方厘米,已知 $BD = 2DA$,$BC = 4BE$,$DF:FC = 3:2$,那么 $\triangle DEF$ 的面积是多少平方厘米?

我的思考
由题意可知,线段之间存在着倍数关系,把线段之间的倍数关系转化为比的关系,通过线段之间比的关系求出线段所在的等高三角形的面积之比,结合已知的 $\triangle ABC$ 的面积,求出 $\triangle DEF$ 的面积。
我的解答
我的发现
我发现解决比和三角形相结合的题目时,先找出等高三角形:底边在同一条直线上,(
顶
)点为同一个点的三角形为等高三角形。再转化比:高相等的两个三角形,面积之比(等于
)底之比。已知线段比可以转化为面积比,已知面积比也可以转化为线段比。答案:我的解答:BD=2DA BD:DA=2:1 $S_{\triangle BDC}$:
$S_{\triangle ADC}=2:1$ $S_{\triangle BDC}=\frac{2}{3}S_{\triangle ABC}$ $BC=4BE$
$BE:BC=1:4$ $EC:BC=3:4$ $S_{\triangle DEC}$:
$S_{\triangle BDC}=3:4$ $S_{\triangle DEC}=\frac{3}{4}S_{\triangle BDC}$ $DF:FC=$
$3:2$ $S_{\triangle DEF}:S_{\triangle CFE}=3:2$ $S_{\triangle DEF}=\frac{3}{5}S_{\triangle DEC}$
$S_{\triangle DEF}=\frac{3}{5} × \frac{3}{4} × \frac{2}{3} × 24=7.2(平方厘米)$
我的发现:顶 等于
$S_{\triangle ADC}=2:1$ $S_{\triangle BDC}=\frac{2}{3}S_{\triangle ABC}$ $BC=4BE$
$BE:BC=1:4$ $EC:BC=3:4$ $S_{\triangle DEC}$:
$S_{\triangle BDC}=3:4$ $S_{\triangle DEC}=\frac{3}{4}S_{\triangle BDC}$ $DF:FC=$
$3:2$ $S_{\triangle DEF}:S_{\triangle CFE}=3:2$ $S_{\triangle DEF}=\frac{3}{5}S_{\triangle DEC}$
$S_{\triangle DEF}=\frac{3}{5} × \frac{3}{4} × \frac{2}{3} × 24=7.2(平方厘米)$
我的发现:顶 等于
如图,在 $\triangle ABC$ 中,$\triangle BDE$、$\triangle DCE$ 和 $\triangle ADC$ 的面积分别是 $45$ 平方厘米、$15$ 平方厘米和 $16$ 平方厘米。$\triangle ADE$ 的面积是多少平方厘米?


答案:$S_{\triangle ADC}:S_{\triangle BDC}=16:(45+15)=4:15$ $AD:$
$BD=4:15$ $S_{\triangle ADE}:S_{\triangle BDE}=4:15$ $S_{\triangle ADE}=$
$\frac{4}{15}S_{\triangle BDE}=\frac{4}{15} × 45=12(平方厘米)$
$BD=4:15$ $S_{\triangle ADE}:S_{\triangle BDE}=4:15$ $S_{\triangle ADE}=$
$\frac{4}{15}S_{\triangle BDE}=\frac{4}{15} × 45=12(平方厘米)$