例 2
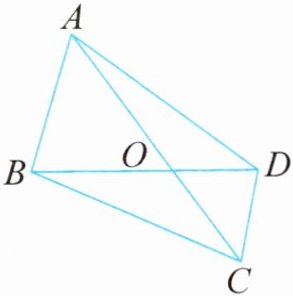
如图,在四边形 $ABCD$ 中,$AO:OC = 3:2$,$BO:OD = 5:3$。那么 $S_{\triangle ABD}:S_{\triangle BCD} = (\quad)$,$S_{\triangle ABC}:S_{\triangle ACD} = (\quad)$。(填最简单的整数比)
我的思考
要想算出 $\triangle ABD$ 与 $\triangle BCD$ 的面积之比,可以根据等高模型直接算出组成 $\triangle ABD$ 的小三角形($\triangle AOB$ 与 $\triangle AOD$)和组成 $\triangle BCD$ 的小三角形($\triangle COB$ 与 $\triangle COD$)的比例关系。$\frac{S_{\triangle AOB}}{S_{\triangle COB}} = \frac{S_{\triangle AOD}}{S_{\triangle COD}} = \frac{AO}{OC}$,则 $\frac{S_{\triangle AOB} + S_{\triangle AOD}}{S_{\triangle COB} + S_{\triangle COD}} = \frac{AO}{OC}$,即 $\frac{S_{\triangle ABD}}{S_{\triangle BCD}} = \frac{AO}{OC}$。$\frac{S_{\triangle AOB}}{S_{\triangle AOD}} = \frac{S_{\triangle COB}}{S_{\triangle COD}} = \frac{BO}{OD}$,则 $\frac{S_{\triangle AOB} + S_{\triangle COB}}{S_{\triangle AOD} + S_{\triangle COD}} = \frac{BO}{OD}$,即 $\frac{S_{\triangle ABC}}{S_{\triangle ACD}} = \frac{BO}{OD}$。也可以采用假设法,假设 $S_{\triangle AOB} = 15$,因为 $AO:OC = 3:2$,所以 $S_{\triangle AOB}:S_{\triangle BOC} = 3:2$,则 $S_{\triangle BOC} = \frac{2}{3}×15 = 10$,又因为 $BO:OD = 5:3$,所以 $S_{\triangle AOB}:S_{\triangle AOD} = S_{\triangle BOC}:S_{\triangle COD} = 5:3$,则 $S_{\triangle AOD} = \frac{3}{5}×15 = 9$,$S_{\triangle COD} = \frac{3}{5}×10 = 6$,所以 $S_{\triangle ABD}:S_{\triangle BCD} = (15 + 9):(10 + 6) = 24:16 = 3:2$,$S_{\triangle ABC}:S_{\triangle ACD} = (15 + 10):(9 + 6) = 25:15 = 5:3$。
我的解答
如图,在四边形 $ABCD$ 中,$AO:OC = 3:2$,$BO:OD = 5:3$。那么 $S_{\triangle ABD}:S_{\triangle BCD} = (\quad)$,$S_{\triangle ABC}:S_{\triangle ACD} = (\quad)$。(填最简单的整数比)

我的思考
要想算出 $\triangle ABD$ 与 $\triangle BCD$ 的面积之比,可以根据等高模型直接算出组成 $\triangle ABD$ 的小三角形($\triangle AOB$ 与 $\triangle AOD$)和组成 $\triangle BCD$ 的小三角形($\triangle COB$ 与 $\triangle COD$)的比例关系。$\frac{S_{\triangle AOB}}{S_{\triangle COB}} = \frac{S_{\triangle AOD}}{S_{\triangle COD}} = \frac{AO}{OC}$,则 $\frac{S_{\triangle AOB} + S_{\triangle AOD}}{S_{\triangle COB} + S_{\triangle COD}} = \frac{AO}{OC}$,即 $\frac{S_{\triangle ABD}}{S_{\triangle BCD}} = \frac{AO}{OC}$。$\frac{S_{\triangle AOB}}{S_{\triangle AOD}} = \frac{S_{\triangle COB}}{S_{\triangle COD}} = \frac{BO}{OD}$,则 $\frac{S_{\triangle AOB} + S_{\triangle COB}}{S_{\triangle AOD} + S_{\triangle COD}} = \frac{BO}{OD}$,即 $\frac{S_{\triangle ABC}}{S_{\triangle ACD}} = \frac{BO}{OD}$。也可以采用假设法,假设 $S_{\triangle AOB} = 15$,因为 $AO:OC = 3:2$,所以 $S_{\triangle AOB}:S_{\triangle BOC} = 3:2$,则 $S_{\triangle BOC} = \frac{2}{3}×15 = 10$,又因为 $BO:OD = 5:3$,所以 $S_{\triangle AOB}:S_{\triangle AOD} = S_{\triangle BOC}:S_{\triangle COD} = 5:3$,则 $S_{\triangle AOD} = \frac{3}{5}×15 = 9$,$S_{\triangle COD} = \frac{3}{5}×10 = 6$,所以 $S_{\triangle ABD}:S_{\triangle BCD} = (15 + 9):(10 + 6) = 24:16 = 3:2$,$S_{\triangle ABC}:S_{\triangle ACD} = (15 + 10):(9 + 6) = 25:15 = 5:3$。
我的解答
答案:3:2 5:3
解析:
解:因为$\frac{AO}{OC}=\frac{3}{2}$,且$\triangle ABD$与$\triangle BCD$分别由$\triangle AOB$、$\triangle AOD$和$\triangle COB$、$\triangle COD$组成,根据等高模型,$\frac{S_{\triangle AOB}}{S_{\triangle COB}}=\frac{S_{\triangle AOD}}{S_{\triangle COD}}=\frac{AO}{OC}=\frac{3}{2}$,所以$\frac{S_{\triangle ABD}}{S_{\triangle BCD}}=\frac{S_{\triangle AOB}+S_{\triangle AOD}}{S_{\triangle COB}+S_{\triangle COD}}=\frac{3}{2}$。
因为$\frac{BO}{OD}=\frac{5}{3}$,且$\triangle ABC$与$\triangle ACD$分别由$\triangle AOB$、$\triangle COB$和$\triangle AOD$、$\triangle COD$组成,根据等高模型,$\frac{S_{\triangle AOB}}{S_{\triangle AOD}}=\frac{S_{\triangle COB}}{S_{\triangle COD}}=\frac{BO}{OD}=\frac{5}{3}$,所以$\frac{S_{\triangle ABC}}{S_{\triangle ACD}}=\frac{S_{\triangle AOB}+S_{\triangle COB}}{S_{\triangle AOD}+S_{\triangle COD}}=\frac{5}{3}$。
$3:2$;$5:3$
因为$\frac{BO}{OD}=\frac{5}{3}$,且$\triangle ABC$与$\triangle ACD$分别由$\triangle AOB$、$\triangle COB$和$\triangle AOD$、$\triangle COD$组成,根据等高模型,$\frac{S_{\triangle AOB}}{S_{\triangle AOD}}=\frac{S_{\triangle COB}}{S_{\triangle COD}}=\frac{BO}{OD}=\frac{5}{3}$,所以$\frac{S_{\triangle ABC}}{S_{\triangle ACD}}=\frac{S_{\triangle AOB}+S_{\triangle COB}}{S_{\triangle AOD}+S_{\triangle COD}}=\frac{5}{3}$。
$3:2$;$5:3$
如图,在四边形 $ABCD$ 中,$BO:OD = 3:2$,$\triangle ABC$ 的面积为 $51$ 平方厘米,则 $\triangle DAC$ 的面积为多少平方厘米?


答案:BO:OD=3:2 $S_{\triangle AOB}:S_{\triangle OAD}=$
3:2 $S_{\triangle BOC}:S_{\triangle COD}=3:2$ $(S_{\triangle AOB}+S_{\triangle BOC}):$
$(S_{\triangle OAD}+S_{\triangle COD})=S_{\triangle ABC}:S_{\triangle DAC}=3:2$
$S_{\triangle DAC}=\frac{2}{3} × 51=34(平方厘米)$
3:2 $S_{\triangle BOC}:S_{\triangle COD}=3:2$ $(S_{\triangle AOB}+S_{\triangle BOC}):$
$(S_{\triangle OAD}+S_{\triangle COD})=S_{\triangle ABC}:S_{\triangle DAC}=3:2$
$S_{\triangle DAC}=\frac{2}{3} × 51=34(平方厘米)$
甲、乙两个圆柱形容器,底面积之比为 $5:3$,甲容器中水深 $9$ 厘米,乙容器中水深 $3$ 厘米,现在往两个容器中注入同样多的水,使它们的水深相等。那么甲容器中的水面上升了多少厘米?
答案:甲、乙两容器中水面上升的高度比:3:5 甲容器中
水面上升高度:(9-3)÷(5-3)×3=9(厘米)
解析 由甲、乙两个容器的底面积之比为5:3和注
入同样多的水可知,甲、乙两个容器中水面上升的高
度比为(1÷5):(1÷3)=3:5,再结合原来两个容
器中水深相差9—3=6(厘米)解决问题。
水面上升高度:(9-3)÷(5-3)×3=9(厘米)
解析 由甲、乙两个容器的底面积之比为5:3和注
入同样多的水可知,甲、乙两个容器中水面上升的高
度比为(1÷5):(1÷3)=3:5,再结合原来两个容
器中水深相差9—3=6(厘米)解决问题。