1. 电信公司推出一种新的业务,通话时间与话费如下表。
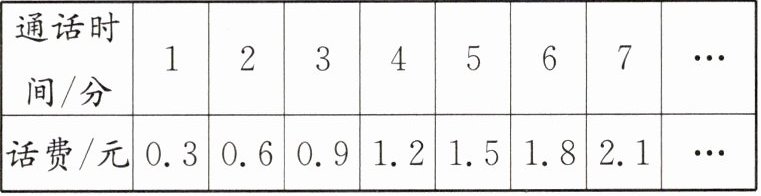
(1)(
(2)通话8分钟需付话费(
(3)话费和相对应的通话时间的比的比值都是(

(1)(
通话时间
)和(话费
)是两种相关联的量,(通话时间
)变化,(话费
)也随着变化。(2)通话8分钟需付话费(
2.4
)元;付2.7元话费可以通话(9
)分钟。(3)话费和相对应的通话时间的比的比值都是(
0.3
),所以话费和通话时间成(正比例
)关系。答案:1.(1)通话时间 话费 通话时间 话费
(2)2.4 9 (3)0.3 正比例
(2)2.4 9 (3)0.3 正比例
2. (1)如果工作效率一定,那么工作总量和(
(2)如果$5x = 8y$($x$和$y$均不为0),那么$y$和$x$(
工作时间
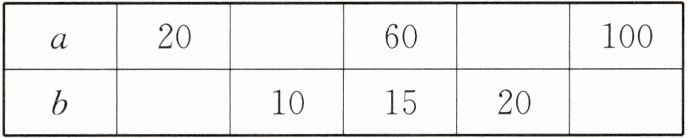
)成正比例。(2)如果$5x = 8y$($x$和$y$均不为0),那么$y$和$x$(
成
)(填“成”或“不成”)正比例。又已知$b$和$a$成正比例关系,请你把下面的表格补充完整。
答案:2.(1)工作时间 (2)成 5 40 80 25
3. 下面(
① 车轮的直径一定,所行的路程和车轮转动的圈数。
② 图上距离和实际距离。
③ 《数学报》的单价一定,总价和份数。
④ 小麦的出粉率一定,小麦的质量和面粉的质量。
①③④
)(填序号)中的两种量成正比例。① 车轮的直径一定,所行的路程和车轮转动的圈数。
② 图上距离和实际距离。
③ 《数学报》的单价一定,总价和份数。
④ 小麦的出粉率一定,小麦的质量和面粉的质量。
答案:3.①③④
4. (2025·宿迁宿城区期末)已知$A = 0.5B$($A$和$B$均为非0的自然数),那么$A$和$B$的最大公因数是(
A
),$A$与$B$(成
)(填“成”或“不成”)正比例。答案:4.A 成
5. 李哲坐电动汽车去外婆家,他每过10分钟看一次里程表上的读数,结果如下:
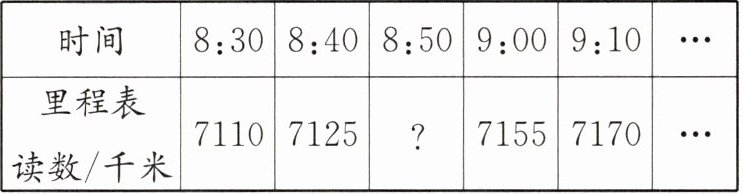
(1)这辆电动汽车的行驶路程和行驶时间(
(2)照表格中的关系,8:50时里程表上的读数应是(
(3)9:10时李哲离外婆家还有30千米。照这样的速度,他(

(1)这辆电动汽车的行驶路程和行驶时间(
成
)正比例。(填“成”或“不成”)(2)照表格中的关系,8:50时里程表上的读数应是(
7140
)千米。(3)9:10时李哲离外婆家还有30千米。照这样的速度,他(
9
)时(30
)分到外婆家。答案:5.(1)成 (2)7140 (3)9 30
6. 亮点原创·如图(单位:平方米)是一个长方形,被两条线段分成四个长方形,其中三个的面积分别是20平方米、25平方米和30平方米,另外一个长方形(图中涂色部分)的面积是(
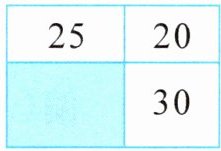
37.5
)平方米。
答案:6.37.5 解析根据长方形的面积=长×宽,可知等宽的两个长方形的面积之比等于长的比,因此,可设涂色部分面积是x平方米,列比例式$\frac{30}{x}=\frac{20}{25},$解得x=37.5。
解析:
设涂色部分面积是$x$平方米。根据等宽的两个长方形面积之比等于长的比,可得$\frac{30}{x}=\frac{20}{25}$,解得$x = \frac{30×25}{20} = 37.5$。
$37.5$
$37.5$
7. 梯形的上、下底之和一定,梯形的面积和高成正比例吗?为什么?
答案:7.成正比例,因为梯形的面积=(上底+下底)×高÷2,所以$\frac{梯形的面积}{高}=($上底+下底)÷2(一定),因此梯形的面积和高成正比例。
解析:
成正比例,因为梯形的面积公式为$S = \frac{(a + b)h}{2}$(其中$a$、$b$分别为上底和下底,$h$为高),已知上、下底之和$a + b$一定,则$\frac{S}{h} = \frac{a + b}{2}$(一定),所以梯形的面积和高成正比例。