1. (1)如果 $ x ÷ y = 5 $($ x $、$ y $ 均不为 $ 0 $),那么 $ x $ 和 $ y $ 成(
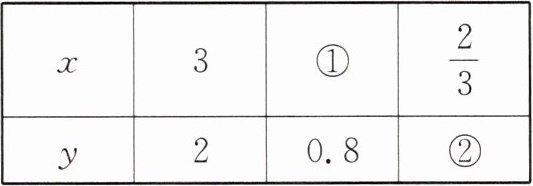
(2)当 $ x $ 和 $ y $ 成正比例时,空格 ① 填(
(3)如果 $ A $ 与 $ B $ 成正比例关系,$ B $ 与 $ C $ 成正比例关系,那么 $ A $ 与 $ C $ 成(
正
)比例。(2)当 $ x $ 和 $ y $ 成正比例时,空格 ① 填(
1.2
),空格 ② 填($\frac{4}{9}$
)。当 $ x $ 和 $ y $ 成反比例时,空格 ① 填(7.5
),空格 ② 填(9
)。
(3)如果 $ A $ 与 $ B $ 成正比例关系,$ B $ 与 $ C $ 成正比例关系,那么 $ A $ 与 $ C $ 成(
正
)比例。答案:1. (1) 正 (2) 1.2 $\frac{4}{9}$ 7.5 9 (3) 正
2. 新趋势 图表信息 要运送 $ 100 $ 吨货物,可选择四种不同的卡车,每种卡车的最大载质量和运送次数如下表。
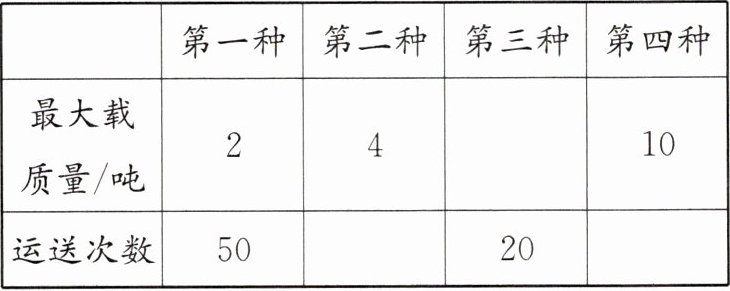
(1)请把表格补充完整。
(2)运送 $ 100 $ 吨货物,卡车的最大载质量和运送次数成(
(3)若用一辆第三种卡车运送货物,它每次的载货量是其最大载质量,请把运送货物的情况填写完整。
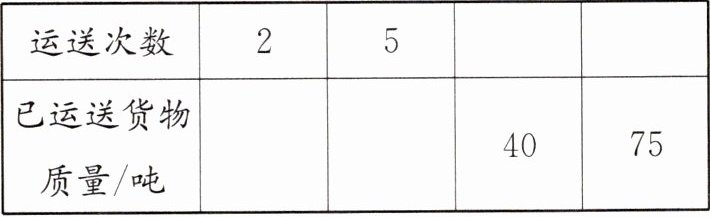
卡车每次载货量一定时,已运送货物质量和运送次数成(

(1)请把表格补充完整。
(2)运送 $ 100 $ 吨货物,卡车的最大载质量和运送次数成(
反
)比例。(3)若用一辆第三种卡车运送货物,它每次的载货量是其最大载质量,请把运送货物的情况填写完整。

卡车每次载货量一定时,已运送货物质量和运送次数成(
正
)比例。答案:2. (1) 25 5 10 (2) 反
(3) 10 25 8 15 正
(3) 10 25 8 15 正
3. 某车间为提高效率,对该车间工人进行加工齿轮效率测试,经统计测算,平均每名工人加工齿轮效率的情况如图。
(1)根据图像判断,加工齿轮的个数和天数成(
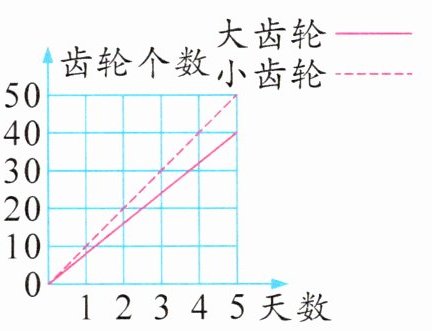
(2)加工小齿轮的效率比大齿轮高(
(3)已知这个车间有工人 $ 85 $ 人,$ 1 $ 个大齿轮和 $ 3 $ 个小齿轮配为一套。为了使大、小齿轮能成套出厂,怎样安排这 $ 85 $ 名工人加工齿轮最合理?
(1)根据图像判断,加工齿轮的个数和天数成(
正
)比例。
(2)加工小齿轮的效率比大齿轮高(
25
)%。(3)已知这个车间有工人 $ 85 $ 人,$ 1 $ 个大齿轮和 $ 3 $ 个小齿轮配为一套。为了使大、小齿轮能成套出厂,怎样安排这 $ 85 $ 名工人加工齿轮最合理?
答案:3. (1) 正 (2) 25 (3) 解:设安排$x$人加工大齿轮,则$(85-x)$人加工小齿轮。 $8x:[10×(85-x)]=1:3$ $x=25$ $85-25=60$(人) 答:安排25人加工大齿轮,安排60人加工小齿轮。
4. 如果甲、乙是两个成反比例的量,那么当甲增加 $ 50 \% $ 时,乙会(
减少$\frac{1}{3}$
)。答案:4. 减少$\frac{1}{3}$ 解析 设甲、乙两个量对应的数分别是$x$、$y$,因为甲、乙是两个成反比例的量,所以$x· y=k$(一定),当甲增加50%时,有$[(1+50\%)x]·(my)=k$,解得$m=\frac{2}{3}$,所以$y$要减少$1-\frac{2}{3}=\frac{1}{3}$。
解析:
设甲、乙两个量对应的数分别是$x$、$y$,因为甲、乙是两个成反比例的量,所以$x· y=k$($k$为一定值)。当甲增加$50\%$时,此时甲为$(1 + 50\%)x = 1.5x$,设此时乙为$my$,则有$1.5x· my = k$。由于$x· y = k$,所以$1.5mxy = xy$,两边同时除以$xy$($xy\neq0$),得$1.5m = 1$,解得$m = \frac{1}{1.5} = \frac{2}{3}$。因此乙减少了$1 - \frac{2}{3} = \frac{1}{3}$。
减少$\frac{1}{3}$
减少$\frac{1}{3}$
5. (2025·淮安市期末改编)冰冰和明明将两个体积相等的铁块,分别浸没在高度相等的甲、乙两个圆柱体水杯中,两铁块全部浸入水中,甲杯水上升了 $ 3 $ 厘米,乙杯水上升的高度比甲杯水多 $ \dfrac{2}{3} $,甲、乙两个水杯的容积之比是多少?(水未溢出)
答案:5. $3×(1+\frac{2}{3})=5$(厘米)
甲水杯底面积:乙水杯底面积$=5:3$
甲水杯容积:乙水杯容积$=5:3$
解析 因为乙杯水上升的高度比甲杯水多$\frac{2}{3}$,所以乙杯水上升了$3×(1+\frac{2}{3})=5$(厘米)。因为两个铁块体积相等,所以甲、乙水杯中水上升的高度与底面积成反比例,即甲水杯底面积:乙水杯底面积$=5:3$。又因为甲、乙两个水杯高度相等,所以它们的容积之比等于底面积之比是$5:3$。
甲水杯底面积:乙水杯底面积$=5:3$
甲水杯容积:乙水杯容积$=5:3$
解析 因为乙杯水上升的高度比甲杯水多$\frac{2}{3}$,所以乙杯水上升了$3×(1+\frac{2}{3})=5$(厘米)。因为两个铁块体积相等,所以甲、乙水杯中水上升的高度与底面积成反比例,即甲水杯底面积:乙水杯底面积$=5:3$。又因为甲、乙两个水杯高度相等,所以它们的容积之比等于底面积之比是$5:3$。