1. 新素养 应用意识 在阳光下,同一时间、同一地点,直立放置几根不同长度的竹竿,测量每根竹竿的长度和影长。情况如下表。
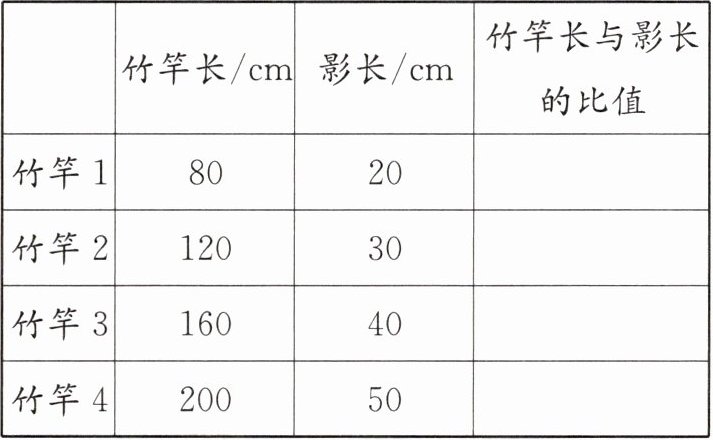
(1)把表格填写完整。
(2)填完上表,你发现了什么?
(3)同学们同时还测量了校园里旗杆的影长是4米。你能算出旗杆的实际高度是多少米吗?
(4)校园的图书馆高5米,这时图书馆的影长大约是(
(5)2小时后,同学们又测量了学校教学楼的影长,用上面的比值计算教学楼的高度,结果准确吗?为什么?

(1)把表格填写完整。
(2)填完上表,你发现了什么?
(3)同学们同时还测量了校园里旗杆的影长是4米。你能算出旗杆的实际高度是多少米吗?
(4)校园的图书馆高5米,这时图书馆的影长大约是(
$\frac{5}{4}$
)米。(5)2小时后,同学们又测量了学校教学楼的影长,用上面的比值计算教学楼的高度,结果准确吗?为什么?
答案:1.(1)4 4 4 4 (2)在同一时间、同一地点,竹竿长与影长的比值相等,它们成正比例。
(3)4×4=16(米$) (4)\frac{5}{4} (5)$不准确,因为2小时后实际高度与测得的影长的比值不再等于4。
(3)4×4=16(米$) (4)\frac{5}{4} (5)$不准确,因为2小时后实际高度与测得的影长的比值不再等于4。
2. 下表是一个数学兴趣小组在同一时间、同一地点测得的一组竹竿的长和竹竿的影长的数据。王老师认为其中有一组的测量误差太大,属于错误的测量数据。
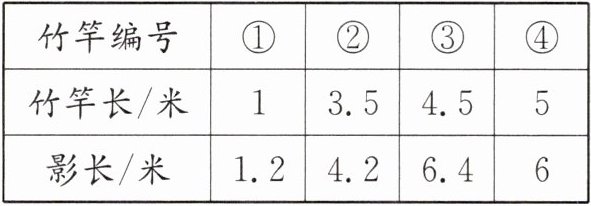
这组错误数据是(

这组错误数据是(
③
)。(填竹竿编号)答案:2. ③
3. (2025·南通海安市期末)新趋势 学科融合 立竿见影的意思是“在阳光下竖起竹竿,立刻就看到了竹竿的影子”,比喻行事能马上看到效果或付出能马上得到收获。乐乐测得某一时间一根高1.8米的竹竿影子长度是0.8米,同一时间附近影长5.6米的大树实际高约(
12.6
)米,用这四个数可以组成比例(1.8:0.8=12.6:5.6(答案不唯一)
)。答案:3.12.6 1.8:0.8=12.6:5.6(答案不唯一)
4. 甲、乙两人进行50米赛跑,当甲到达终点时,乙在甲后面10米。如果甲、乙两人各自的速度不变,要使两人同时到达终点,甲的起跑线应后移(
12.5
)米。答案:4.12.5 解析 当甲到终点时,乙在甲后面10米,他们所用的时间相同,所以甲、乙的路程比等于他们的速度比,即为50:(50-10)=5:4;要使两人同时到达终点,此时甲、乙的路程比仍等于他们的速度比。又因他们两人的速度不变,可设甲的起跑线应比原来后移x米,列出比例式(50+x):50=5:4,解得x=12.5。
解析:
当甲到达终点时,乙跑的路程为$50 - 10=40$米,此时甲、乙路程比为$50:40 = 5:4$,即速度比为$5:4$。
设甲的起跑线应后移$x$米,要使两人同时到达终点,此时甲跑的路程为$(50 + x)$米,乙跑的路程为$50$米,因为速度不变,路程比等于速度比,所以$(50 + x):50=5:4$。
由比例性质可得$4(50 + x)=5×50$,即$200 + 4x=250$,$4x=50$,解得$x = 12.5$。
12.5
设甲的起跑线应后移$x$米,要使两人同时到达终点,此时甲跑的路程为$(50 + x)$米,乙跑的路程为$50$米,因为速度不变,路程比等于速度比,所以$(50 + x):50=5:4$。
由比例性质可得$4(50 + x)=5×50$,即$200 + 4x=250$,$4x=50$,解得$x = 12.5$。
12.5
5. 萌萌利用影长测量学校旗杆的高度。在某一时刻,旗杆的影子一部分在地面上,另一部分在教学楼的墙上,测得其长度分别为9.6米和2米(如图),在同一时刻测得1米长的竹竿的影长为1.2米。求学校旗杆的高度。
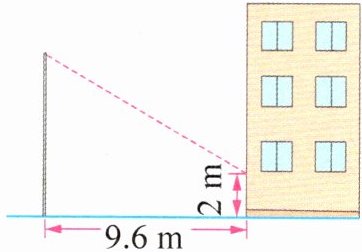

答案:5.1.2÷1×2=2.4(米) (2.4+9.6)×1÷1.2=10(米) 解析 根据题意,同一时刻物体的高度和影子的长度成正比例关系,所以要求学校旗杆的高度,先求此时其影子的长度。根据1米长的竹竿影长为1.2米,可得2米高的墙的影长为1.2÷1×2=2.4(米),则旗杆的影长为2.4+9.6=12(米),利用同一时刻旗杆的高度和影长的比值等于竹竿的高度和影长的比值即可求解。
解析:
1.2÷1×2=2.4(米)
(2.4+9.6)×1÷1.2=10(米)
答:学校旗杆的高度为10米。
(2.4+9.6)×1÷1.2=10(米)
答:学校旗杆的高度为10米。