1. (1)在镜子中看见的电子钟上的时间是“02:51”,正确的时间应是(
(2)一个圆的周长是 37.68 厘米,按 2:1 的比放大后,圆的面积变成了(
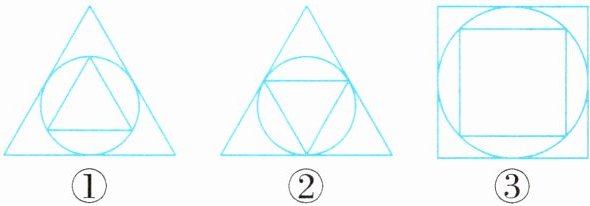
(3)新素养 几何直观 图①中的两个三角形都是等边三角形,如果把小三角形绕它的中心旋转 180°,就可以得到图②。从图②中可以看出,小三角形的面积是大三角形面积的(
 ]
]
12:50
)。(2)一个圆的周长是 37.68 厘米,按 2:1 的比放大后,圆的面积变成了(
452.16
)平方厘米。(3)新素养 几何直观 图①中的两个三角形都是等边三角形,如果把小三角形绕它的中心旋转 180°,就可以得到图②。从图②中可以看出,小三角形的面积是大三角形面积的(
25
)%,则图③中小正方形的面积是大正方形面积的(50
)%。 ]
]答案:1.(1)12:50 (2)452.16 (3)25 50
2. 新情境 传统文化 被列为非物质文化遗产的陕北剪纸,通过现场操作等多种形式,让市民体验到了传统技艺的妙趣。某市民将一个正方形彩纸依次按如下图①②所示的方式对折,然后沿图③中的虚线裁剪,则将图③的彩纸展开铺平后的图形是(
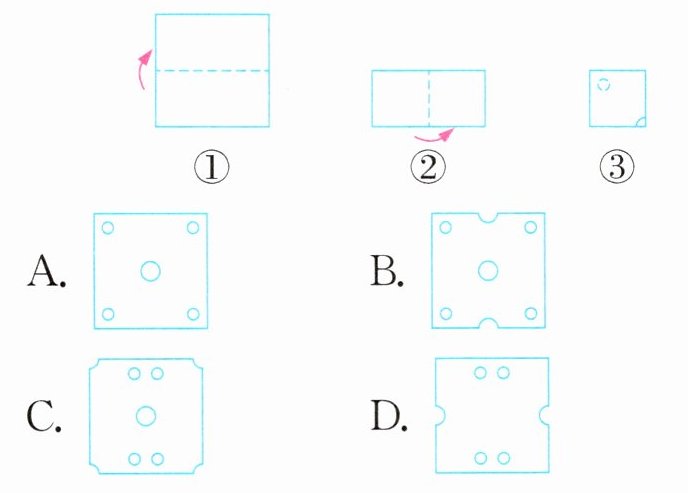
D
)。
答案:2.D
3. (1)把通过平移就可以与图形 A 完全重合的图形涂成灰色。
(2)把能与图形 A 形成轴对称的图形涂成蓝色。
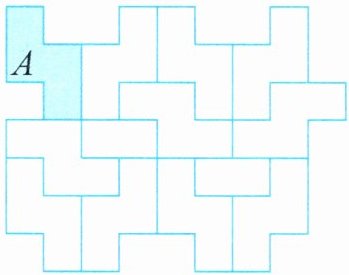
(2)把能与图形 A 形成轴对称的图形涂成蓝色。

答案:
3.(1)(2)如图。
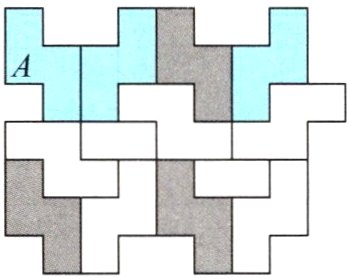
3.(1)(2)如图。

4. 把一个长方形(长 4 厘米、宽 3 厘米、对角线长 5 厘米)按下图进行翻转,翻转一次到①,翻转两次到②……点 A 翻转到点 A'时所走过的路程是(
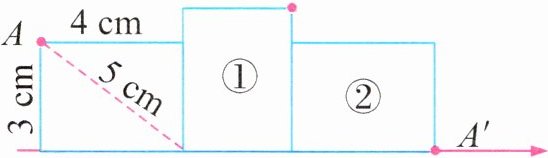 ]
]
14.13
)厘米。 ]
]答案:4.14.13
5. 如图,大圆的直径为 10 厘米,小圆的直径为 2 厘米。如果让小圆沿着大圆圆周外侧滚动一圈,小圆扫过的区域的面积是(
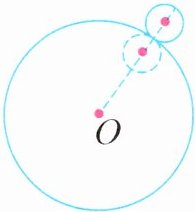 ]
]
75.36
)平方厘米。如果让小圆沿着大圆圆周内侧滚动一圈,小圆扫过的区域的面积是(50.24
)平方厘米。 ]
]答案:5.75.36 50.24 解析:大圆半径为10÷2=5(厘米),小圆沿着大圆圆周外侧滚动时,小圆滚动的区域是半径为5+2=7(厘米)和5厘米的同心圆中的环形,面积为$3.14×(7^2 - 5^2)=75.36($平方厘米)。小圆沿着大圆圆周内侧滚动时,小圆滚动的区域是半径为5厘米和5 - 2=3(厘米)的同心圆中的环形,面积为$3.14×(5^2 - 3^2)=50.24($平方厘米)。
解析:
解:大圆半径:$10÷2 = 5$(厘米)
小圆半径:$2÷2 = 1$(厘米)
外侧滚动:
外圆半径:$5 + 2 = 7$(厘米)
环形面积:$3.14×(7^2 - 5^2)=3.14×(49 - 25)=3.14×24 = 75.36$(平方厘米)
内侧滚动:
内圆半径:$5 - 2 = 3$(厘米)
环形面积:$3.14×(5^2 - 3^2)=3.14×(25 - 9)=3.14×16 = 50.24$(平方厘米)
75.36;50.24
小圆半径:$2÷2 = 1$(厘米)
外侧滚动:
外圆半径:$5 + 2 = 7$(厘米)
环形面积:$3.14×(7^2 - 5^2)=3.14×(49 - 25)=3.14×24 = 75.36$(平方厘米)
内侧滚动:
内圆半径:$5 - 2 = 3$(厘米)
环形面积:$3.14×(5^2 - 3^2)=3.14×(25 - 9)=3.14×16 = 50.24$(平方厘米)
75.36;50.24
6. 如图,三角形 ABC 中,底和高都是 6 厘米。从点 A 分离出点 A',点 A 不动,点 A'和点 C 同时以 0.5 厘米/秒的速度向右平移,形成一个梯形。经过多少秒后,梯形的面积将达到 42 平方厘米?
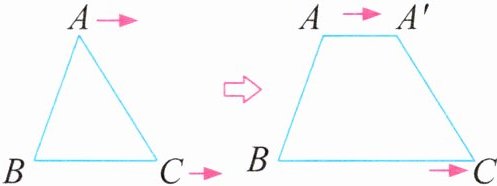

答案:6.42×2÷6=14(厘米) (14 - 6)÷2=4(厘米) 4÷0.5=8(秒) 解析:根据梯形的面积是42平方厘米,高是6厘米,可求出梯形上、下底的和为14厘米,由题意可知下底比上底长6厘米,根据和差问题的公式可求出梯形的上底是4厘米,最后得出梯形面积达到42平方厘米所经过的时间是4÷0.5=8(秒)。