1. (1)小明买电影票先选的位置是$(7,8)$,若他想往前坐一个位置,则他该选位置( , )。
(2)聪聪面向南偏东$20^{\circ}$方向,当他向右转$180^{\circ}$时,他面向(
(2)聪聪面向南偏东$20^{\circ}$方向,当他向右转$180^{\circ}$时,他面向(
北
)偏(西
)(20
)$^{\circ}$方向。答案:1.(1)(7,7) (2)北 西 20
2. 如图,下面各点中,在直线$l$上的是点(
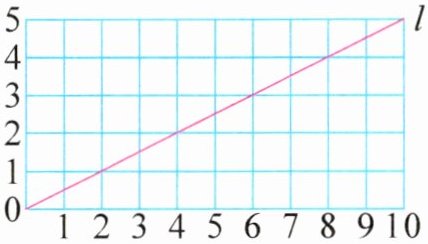
A.$(\dfrac{1}{2}x,x)$
B.$(x,\dfrac{1}{4}x)$
C.$(2x,x)$
C
)。
A.$(\dfrac{1}{2}x,x)$
B.$(x,\dfrac{1}{4}x)$
C.$(2x,x)$
答案:2.C
3. 下面是奇奇家附近的平面图。

(1)奇奇从家出发,先向(
(2)如果奇奇打算按照原路步行回家,请你描述他回家的路线。
(3)书店在银行的南偏西$40^{\circ}$方向$400$m 处,那么银行在书店的(

(1)奇奇从家出发,先向(
东
)步行(300
)m 到达超市,再向(北
)偏(东
)(50
)$^{\circ}$方向步行(500
)m 到达博物馆,最后向(东
)步行(400
)m 到达医院。(2)如果奇奇打算按照原路步行回家,请你描述他回家的路线。
(3)书店在银行的南偏西$40^{\circ}$方向$400$m 处,那么银行在书店的(
北偏东40°
)方向(400
)m 处,在图中画出银行的大概位置。答案:
3.(1)东 300 北 东 50 500 东 400
(2)奇奇从医院出发,先向西步行400m到达博物馆,再向南偏西50°方向步行500m到达超市,最后向西步行300m到达家。
(3)北偏东40° 400

3.(1)东 300 北 东 50 500 东 400
(2)奇奇从医院出发,先向西步行400m到达博物馆,再向南偏西50°方向步行500m到达超市,最后向西步行300m到达家。
(3)北偏东40° 400

4. (2025·淮安市期末)下图中涂色三角形是空白三角形沿着对称轴画出的轴对称图形。根据图中信息,请用数对表示出点$A$、$B$的位置:$A$( , ),$B$( , )。


答案:4.(8,4) (12,1)
解析:
(8,4);(12,1)
5. 在方格纸上的一个三角形的两个顶点用数对表示分别是$(5,7)$和$(8,4)$。若这个三角形是等腰三角形,则它的另一个顶点用数对表示不可能是()。
A.$(3,7)$
B.$(8,7)$
C.$(5,1)$
D.$(11,7)$
A.$(3,7)$
B.$(8,7)$
C.$(5,1)$
D.$(11,7)$
答案:A
解析:
已知两点A(5,7)、B(8,4),计算AB²=(8-5)²+(4-7)²=9+9=18。
选项A:P(3,7),PA²=(5-3)²+(7-7)²=4,PB²=(8-3)²+(4-7)²=25+9=34,PA²≠PB²≠AB²,不是等腰三角形。
选项B:P(8,7),PA²=(8-5)²+(7-7)²=9,PB²=(8-8)²+(7-4)²=9,PA²=PB²,是等腰三角形。
选项C:P(5,1),PA²=(5-5)²+(1-7)²=36,PB²=(8-5)²+(4-1)²=18,PB²=AB²,是等腰三角形。
选项D:P(11,7),PA²=(11-5)²+(7-7)²=36,PB²=(8-11)²+(4-7)²=18,PB²=AB²,是等腰三角形。
选项A:P(3,7),PA²=(5-3)²+(7-7)²=4,PB²=(8-3)²+(4-7)²=25+9=34,PA²≠PB²≠AB²,不是等腰三角形。
选项B:P(8,7),PA²=(8-5)²+(7-7)²=9,PB²=(8-8)²+(7-4)²=9,PA²=PB²,是等腰三角形。
选项C:P(5,1),PA²=(5-5)²+(1-7)²=36,PB²=(8-5)²+(4-1)²=18,PB²=AB²,是等腰三角形。
选项D:P(11,7),PA²=(11-5)²+(7-7)²=36,PB²=(8-11)²+(4-7)²=18,PB²=AB²,是等腰三角形。
6. 同学们参加运动会,组成一个方阵,小强的位置不管从前后左右看都是$(10,10)$,这个方阵一共有()人。
答案:361
解析:
因为小强不管从前后左右看都是第10个,那么方阵的行数和列数都应为$10 + 10 - 1=19$(人),方阵总人数为行数乘以列数,即$19×19 = 361$(人)。
7. 实验小学举行运动会,全体运动员的编号是从$1$开始的连续的自然数,他们按下图中实线和箭头所示,从第一行第一列开始,按照编号从小到大的顺序排成一个正方形方阵。奇奇的编号是$30$,他排在第$6$列第$3$行,该校全体运动员一共有多少人?


答案:设正方形方阵为$ n $行$ n $列,总人数为$ n^2 $。
奇奇在第3行第6列,编号30。假设方阵中奇数行从左到右排列,偶数行从右到左排列(蛇形排列)。第3行为奇数行,从左到右排列,其编号为前两行总数加列数。前两行共有$ 2n $人,故第3行第6列编号为$ 2n + 6 $。
由题意得:$ 2n + 6 = 30 $,解得$ n = 12 $。
总人数为$ n^2 = 12^2 = 144 $。
144
奇奇在第3行第6列,编号30。假设方阵中奇数行从左到右排列,偶数行从右到左排列(蛇形排列)。第3行为奇数行,从左到右排列,其编号为前两行总数加列数。前两行共有$ 2n $人,故第3行第6列编号为$ 2n + 6 $。
由题意得:$ 2n + 6 = 30 $,解得$ n = 12 $。
总人数为$ n^2 = 12^2 = 144 $。
144