1. 在括号里填“一定”或“不一定”。
(1)有一个角是 $45^{\circ}$ 的等腰三角形(
(2)拉动平行四边形的一个角,使它变成直角,这时的平行四边形(
(1)有一个角是 $45^{\circ}$ 的等腰三角形(
不一定
)是直角三角形。(2)拉动平行四边形的一个角,使它变成直角,这时的平行四边形(
一定
)是长方形。答案:1.(1)不一定 (2)一定
2. 用5,6,7这三个数字组成不同的三位数,结果出现奇数的可能性比出现偶数的可能性(
大
)(填“大”或“小”)。如果用数字0代替其中的数字(6
),组成的三位数中出现奇数与偶数的可能性相等。答案:2.大 6
3. (1)新趋势 学科融合 在日常生活中,我们经常使用一些成语来形容事情发生的可能性的大小,如:① 平分秋色;② 百发百中;③ 天方夜谭;④ 十拿九稳。将它们按可能性从小到大排列为(
A. ③<①<④<②
B. ②>④>①>③
C. ③<①<②<④
(2)(2025·无锡新吴区期末)旋转转盘的指针,如果指针停在质数的位置,就能获得奖品。菲菲第一次旋转的结果如下图所示,她没有得奖。如果再旋转一次,她(
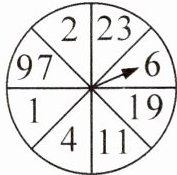
A. 得奖和不得奖的可能性一样大
B. 得奖的可能性小
C. 得奖的可能性大
D. 不可能得奖
A
)。A. ③<①<④<②
B. ②>④>①>③
C. ③<①<②<④
(2)(2025·无锡新吴区期末)旋转转盘的指针,如果指针停在质数的位置,就能获得奖品。菲菲第一次旋转的结果如下图所示,她没有得奖。如果再旋转一次,她(
C
)。
A. 得奖和不得奖的可能性一样大
B. 得奖的可能性小
C. 得奖的可能性大
D. 不可能得奖
答案:3.(1)A (2)C
4. 口袋中有4个红球、5个黄球和6个黑球,至少摸出(
12
)个球才能保证有红球。答案:4.12
5. 有4张卡片$\overline{3}$、$\overline{5}$、$\overline{2}$、$\overline{8}$,从中任意抽取2张,公平的游戏规则是(
A.和是2的倍数,甲胜,否则乙胜
B.积是2的倍数,甲胜;积是3的倍数,乙胜
C.积是3的倍数,甲胜,否则乙胜
C
)。A.和是2的倍数,甲胜,否则乙胜
B.积是2的倍数,甲胜;积是3的倍数,乙胜
C.积是3的倍数,甲胜,否则乙胜
答案:5.C
解析:
从4张卡片中任意抽取2张,所有可能的组合及对应的和与积如下:
3和5:和=8,积=15
3和2:和=5,积=6
3和8:和=11,积=24
5和2:和=7,积=10
5和8:和=13,积=40
2和8:和=10,积=16
选项A:和是2的倍数的情况有(3,5)、(2,8),共2种;否则有4种,不公平。
选项B:积是2的倍数的情况有(3,2)、(3,8)、(5,2)、(5,8)、(2,8),共5种;积是3的倍数的情况有(3,5)、(3,2)、(3,8),共3种,不公平。
选项C:积是3的倍数的情况有(3,5)、(3,2)、(3,8),共3种;否则有3种,公平。
C
3和5:和=8,积=15
3和2:和=5,积=6
3和8:和=11,积=24
5和2:和=7,积=10
5和8:和=13,积=40
2和8:和=10,积=16
选项A:和是2的倍数的情况有(3,5)、(2,8),共2种;否则有4种,不公平。
选项B:积是2的倍数的情况有(3,2)、(3,8)、(5,2)、(5,8)、(2,8),共5种;积是3的倍数的情况有(3,5)、(3,2)、(3,8),共3种,不公平。
选项C:积是3的倍数的情况有(3,5)、(3,2)、(3,8),共3种;否则有3种,公平。
C
6. 在两个相同的袋子中,都放入编号分别为1,2,3,4,5的五个小球,这些小球的形状、大小完全相同。从两个袋子中各任意摸出一个小球,计算两个小球编号之和。
(1)两个小球编号之和最大是(
(2)两个小球编号之和是(
(1)两个小球编号之和最大是(
10
),最小是(2
)。(2)两个小球编号之和是(
6
)的可能性最大。(填数字)答案:
6.(1)10 2 (2)6 解析 从两个袋子中各任意摸出一个小球,两个小球编号之和可能出现的结果如下表:

从表中可以看出,两个小球编号之和最大是10,最小是2,而编号之和是6的有5种情况,出现的次数最多,所以编号之和是6的可能性最大。
6.(1)10 2 (2)6 解析 从两个袋子中各任意摸出一个小球,两个小球编号之和可能出现的结果如下表:

从表中可以看出,两个小球编号之和最大是10,最小是2,而编号之和是6的有5种情况,出现的次数最多,所以编号之和是6的可能性最大。
7. 端午是我国传统佳节,婉婉带了5个粽子(除馅不同外,其他均相同),其中有2个肉粽、2个红枣粽和1个豆沙粽,准备从中任意拿出2个送给她的好朋友小张,小张拿到2个粽子是一荤一素的可能性大,还是全素的可能性大?
答案:7.一荤一素的可能性大。 解析 设肉粽为A₁,A₂,红枣粽为B₁,B₂,豆沙粽为C,从中拿2个,所有的可能为:A₁A₂、A₁B₁、A₁B₂、A₁C、A₂B₁、A₂B₂、A₂C、B₁B₂、B₁C、B₂C,一荤一素的有6种,全素的有3种。
解析:
设肉粽为$A_1$,$A_2$,红枣粽为$B_1$,$B_2$,豆沙粽为$C$。从中任拿2个,所有可能情况为:$A_1A_2$、$A_1B_1$、$A_1B_2$、$A_1C$、$A_2B_1$、$A_2B_2$、$A_2C$、$B_1B_2$、$B_1C$、$B_2C$,共10种。
一荤一素的情况有:$A_1B_1$、$A_1B_2$、$A_1C$、$A_2B_1$、$A_2B_2$、$A_2C$,共6种。
全素的情况有:$B_1B_2$、$B_1C$、$B_2C$,共3种。
因为$6>3$,所以一荤一素的可能性大。
一荤一素的情况有:$A_1B_1$、$A_1B_2$、$A_1C$、$A_2B_1$、$A_2B_2$、$A_2C$,共6种。
全素的情况有:$B_1B_2$、$B_1C$、$B_2C$,共3种。
因为$6>3$,所以一荤一素的可能性大。