5. 一个圆柱和一个圆锥等底等高,如果圆柱的体积是24立方厘米,那么圆锥的体积是(
8
)立方厘米;如果圆锥的体积比圆柱的体积少24立方厘米,那么圆柱的体积是(36
)立方厘米。答案:5. 8 36
6. 一个圆柱,高是4厘米,如果高增加1厘米,表面积就比原来增加31.4平方厘米。原来圆柱的侧面积是(
125.6
)平方厘米,体积是(314
)立方厘米。答案:6. 125.6 314
解析:
圆柱的高增加1厘米,表面积增加的部分就是高为1厘米的圆柱的侧面积。
圆柱侧面积公式为$S = 2\pi rh$,其中$r$为底面半径,$h$为高。
已知表面积增加$31.4$平方厘米,高增加$1$厘米,可得:
$2\pi r×1 = 31.4$,则$2\pi r=31.4$。
原来圆柱的高是$4$厘米,原来圆柱的侧面积为:
$S_{侧}=2\pi r×4 = 31.4×4 = 125.6$(平方厘米)。
由$2\pi r = 31.4$,可得$r=\frac{31.4}{2\pi}=\frac{31.4}{2×3.14}=5$(厘米)。
圆柱体积公式为$V=\pi r^2h$,原来圆柱的体积为:
$V = 3.14×5^2×4=3.14×25×4 = 314$(立方厘米)。
125.6;314
圆柱侧面积公式为$S = 2\pi rh$,其中$r$为底面半径,$h$为高。
已知表面积增加$31.4$平方厘米,高增加$1$厘米,可得:
$2\pi r×1 = 31.4$,则$2\pi r=31.4$。
原来圆柱的高是$4$厘米,原来圆柱的侧面积为:
$S_{侧}=2\pi r×4 = 31.4×4 = 125.6$(平方厘米)。
由$2\pi r = 31.4$,可得$r=\frac{31.4}{2\pi}=\frac{31.4}{2×3.14}=5$(厘米)。
圆柱体积公式为$V=\pi r^2h$,原来圆柱的体积为:
$V = 3.14×5^2×4=3.14×25×4 = 314$(立方厘米)。
125.6;314
7. 一个圆锥形容器,底面半径是5厘米,高是18厘米,在里面装满水,倒入与它等底等高的圆柱形容器里,这时水面高(
6
)厘米,还可以倒入(942
)毫升水。(忽略容器壁厚度)答案:7. 6 942
解析:
圆锥体积:$\frac{1}{3} × \pi × 5^2 × 18 = 150\pi$(立方厘米)
圆柱底面积:$\pi × 5^2 = 25\pi$(平方厘米)
水面高度:$150\pi ÷ 25\pi = 6$(厘米)
圆柱体积:$25\pi × 18 = 450\pi$(立方厘米)
还可倒入体积:$450\pi - 150\pi = 300\pi = 300 × 3.14 = 942$(立方厘米)= 942毫升
6,942
圆柱底面积:$\pi × 5^2 = 25\pi$(平方厘米)
水面高度:$150\pi ÷ 25\pi = 6$(厘米)
圆柱体积:$25\pi × 18 = 450\pi$(立方厘米)
还可倒入体积:$450\pi - 150\pi = 300\pi = 300 × 3.14 = 942$(立方厘米)= 942毫升
6,942
8. 有一个棱长为6分米的正方体铁块,如果将它熔铸成一个圆柱,那么这个圆柱的体积是(
216
)立方分米;如果将这个正方体铁块削成一个最大的圆锥,那么这个圆锥的体积是(56.52
)立方分米。答案:8. 216 56.52
9. 一个圆柱的高不变,底面半径扩大到原来的2倍,它的体积将扩大到原来的(
4
)倍;一个圆锥的底面半径扩大到原来的3倍,高也扩大到原来的3倍,它的体积将扩大到原来的(27
)倍。答案:9. 4 27
10. 亮点原创 有大、小两种玻璃球,放入装有同样多水的相同圆柱形容器中,如下图。
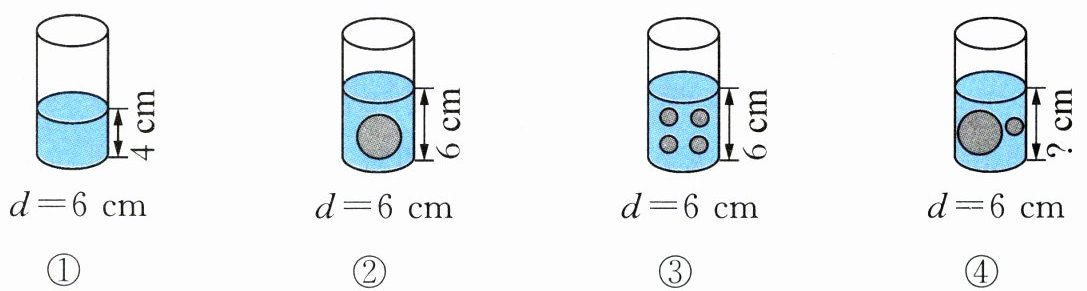
(1)大球的体积是(
(2)大球与小球的体积比是(
(3)图④中水面的高度是(

(1)大球的体积是(
56.52
)立方厘米。(2)大球与小球的体积比是(
4:1
)。(3)图④中水面的高度是(
6.5
)厘米。答案:10. (1) $56.52$ 解析 由题图①和题图②可知,升高的$(6 - 4)$厘米的这部分水的体积就是一个大球的体积,即$3.14×(6÷2)^2×(6 - 4)=56.52$(立方厘米)。
(2) $4:1$ 解析 由题图①、题图②和题图③的水面高度可知,1个大球的体积等于4个小球的体积,大球、小球的体积比为$4:1$。 (3) $6.5$ 解析 由题图①和题图②可知,放入1个大球水面上升$6 - 4=2$(厘米),由题图①和题图③可知,放入1个大球和1个小球水面要上升$2 + 0.5=2.5$(厘米),题图④中水面的高度为$4 + 2.5=6.5$(厘米)。
(2) $4:1$ 解析 由题图①、题图②和题图③的水面高度可知,1个大球的体积等于4个小球的体积,大球、小球的体积比为$4:1$。 (3) $6.5$ 解析 由题图①和题图②可知,放入1个大球水面上升$6 - 4=2$(厘米),由题图①和题图③可知,放入1个大球和1个小球水面要上升$2 + 0.5=2.5$(厘米),题图④中水面的高度为$4 + 2.5=6.5$(厘米)。
11. 如图,一个饮料瓶的内直径是8cm,这个饮料瓶的容积相当于一个底面内直径是8cm、高是(
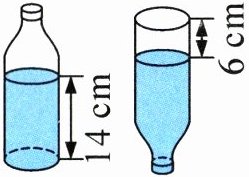
20
)cm的圆柱形容器的容积。
答案:11. $20$ 解析 由题图可知饮料瓶的容积是一个高为$14cm$、底面直径为$8cm$的圆柱和一个高为$6cm$、底面直径为$8cm$的圆柱的体积之和,即相当于一个底面内直径是$8cm$、高是$14 + 6=20(cm)$的圆柱形容器的容积。
解析:
14 + 6 = 20(cm)
三、判断题。(每题1分,共5分)
1. 从圆锥的顶点到底面上的任意一点的距离就是圆锥的高。 (
2. 圆柱的底面半径扩大到原来的2倍,高不变,则侧面积扩大到原来的4倍。 (
3. 把一个圆柱削成一个最大的圆锥,削掉部分的体积是圆锥体积的2倍。 (
4. 底面积和高都相等的长方体和圆锥,长方体的体积是圆锥体积的3倍。 (
5. 圆柱的侧面展开后不可能得到一个平行四边形。 (
1. 从圆锥的顶点到底面上的任意一点的距离就是圆锥的高。 (
×
)2. 圆柱的底面半径扩大到原来的2倍,高不变,则侧面积扩大到原来的4倍。 (
×
)3. 把一个圆柱削成一个最大的圆锥,削掉部分的体积是圆锥体积的2倍。 (
√
)4. 底面积和高都相等的长方体和圆锥,长方体的体积是圆锥体积的3倍。 (
√
)5. 圆柱的侧面展开后不可能得到一个平行四边形。 (
×
)答案:1. × 2. × 3. √ 4. √ 5. ×
1. 一个圆柱的侧面展开后正好是一个正方形,那么圆柱的高和它底面直径的比是(
A.$1:1$
B.$1:π$
C.$2:π$
D.$π:1$
D
)。A.$1:1$
B.$1:π$
C.$2:π$
D.$π:1$
答案:1. D
解析:
设圆柱底面直径为$d$,则底面周长为$\pi d$。因为圆柱侧面展开后是正方形,所以圆柱的高$h$等于底面周长,即$h = \pi d$。则圆柱的高和底面直径的比为$h:d=\pi d:d=\pi:1$。
D
D