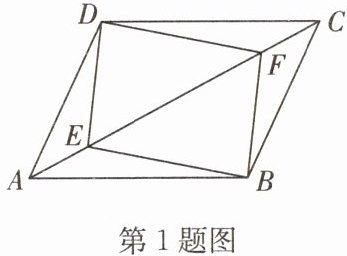
1. 如图,四边形ABCD是平行四边形,DE//BF,且分别交对角线AC于点E,F,连接DF,BE.
求证:(1)AE=CF;
(2)∠DFE=∠BEF.
求证:(1)AE=CF;
(2)∠DFE=∠BEF.

答案:1.证明:(1)
∵四边形ABCD是平行四边形,
∴AD//BC,AD=BC,
∴∠DAC=∠BCA.
∵DE//BF,
∴∠DEF=∠BFE,
∴∠AED=∠CFB.
在△ADE和△CBF中,$\{\begin{array}{l} ∠ DAE=∠ BCF,\\ ∠ AED=∠ CFB,\\ AD=CB,\end{array} $
∴△ADE≌△CBF(AAS),
∴AE=CF;
(2)
∵△ADE≌△CBF,
∴DE=FB.
又
∵DE//BF,
∴四边形DEBF为平行四边形,
∴DF//EB,
∴∠DFE=∠BEF;
∵四边形ABCD是平行四边形,
∴AD//BC,AD=BC,
∴∠DAC=∠BCA.
∵DE//BF,
∴∠DEF=∠BFE,
∴∠AED=∠CFB.
在△ADE和△CBF中,$\{\begin{array}{l} ∠ DAE=∠ BCF,\\ ∠ AED=∠ CFB,\\ AD=CB,\end{array} $
∴△ADE≌△CBF(AAS),
∴AE=CF;
(2)
∵△ADE≌△CBF,
∴DE=FB.
又
∵DE//BF,
∴四边形DEBF为平行四边形,
∴DF//EB,
∴∠DFE=∠BEF;
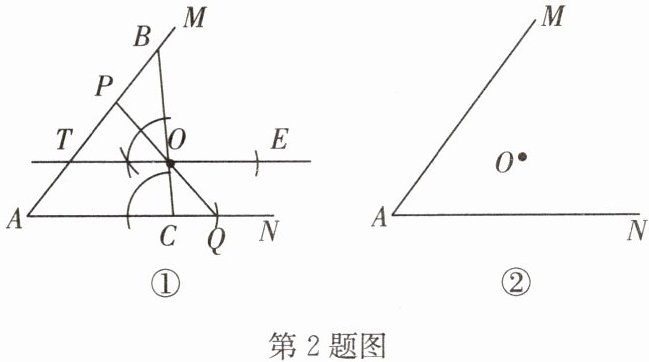
2. (2024·徐州期中)如图,O是∠MAN内一点,求作线段PQ,使点P,Q分别在射线AM,AN上,且O是PQ的中点(要求:用无刻度的直尺和圆规作图,保留作图痕迹).
小亮的作法如下:如图①,过点O作直线BC分别交AM,AN于点B,C. 作∠BOT=∠BCA,且OT交AM于点T,在射线TO上截取OE=OT,在AN上截取AQ,使得AQ=TE,连接QO,并延长交AM于点P,线段PQ即为所求.
(1)请证明小亮作法的正确性;
(2)请你在图②中再设计另一种尺规作图的方法(保留作图痕迹,不写作法).
小亮的作法如下:如图①,过点O作直线BC分别交AM,AN于点B,C. 作∠BOT=∠BCA,且OT交AM于点T,在射线TO上截取OE=OT,在AN上截取AQ,使得AQ=TE,连接QO,并延长交AM于点P,线段PQ即为所求.
(1)请证明小亮作法的正确性;
(2)请你在图②中再设计另一种尺规作图的方法(保留作图痕迹,不写作法).

答案:
(1)证明:连接QE.由作图过程可知OT//AN,AQ=TE,
∴四边形ATEQ是平行四边形,
∴AT//QE,
∴∠OTP=∠OEQ.
∵OT=OE,∠TOP=∠EOQ,
∴△OTP≌△OEQ(ASA),
∴OP=OQ.
(2)解:如答图,线段PQ即为所求,O是PQ的中点.
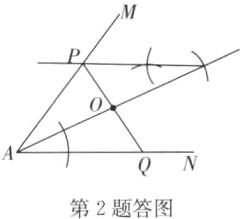
(1)证明:连接QE.由作图过程可知OT//AN,AQ=TE,
∴四边形ATEQ是平行四边形,
∴AT//QE,
∴∠OTP=∠OEQ.
∵OT=OE,∠TOP=∠EOQ,
∴△OTP≌△OEQ(ASA),
∴OP=OQ.
(2)解:如答图,线段PQ即为所求,O是PQ的中点.
