1. 在$□ ABCD$中,$BC$边上的高为$4$,$AB = 5$,$AC = 2\sqrt{5}$,则$□ ABCD$的周长为
12或20
.答案:1. 12或20
解析:
解:分两种情况讨论:
情况一:高在BC边上
过点A作AE⊥BC于E,则AE=4。
在Rt△ABE中,AB=5,AE=4,
由勾股定理得:BE=$\sqrt{AB^2-AE^2}=\sqrt{5^2-4^2}=3$。
在Rt△AEC中,AC=$2\sqrt{5}$,AE=4,
由勾股定理得:EC=$\sqrt{AC^2-AE^2}=\sqrt{(2\sqrt{5})^2-4^2}=\sqrt{20-16}=2$。
此时BC=BE+EC=3+2=5,
周长=2(AB+BC)=2×(5+5)=20。
情况二:高在BC延长线上
过点A作AE⊥BC交BC延长线于E,则AE=4。
同理,BE=3,EC=2,
此时BC=BE-EC=3-2=1,
周长=2(AB+BC)=2×(5+1)=12。
综上,□ABCD的周长为12或20。
情况一:高在BC边上
过点A作AE⊥BC于E,则AE=4。
在Rt△ABE中,AB=5,AE=4,
由勾股定理得:BE=$\sqrt{AB^2-AE^2}=\sqrt{5^2-4^2}=3$。
在Rt△AEC中,AC=$2\sqrt{5}$,AE=4,
由勾股定理得:EC=$\sqrt{AC^2-AE^2}=\sqrt{(2\sqrt{5})^2-4^2}=\sqrt{20-16}=2$。
此时BC=BE+EC=3+2=5,
周长=2(AB+BC)=2×(5+5)=20。
情况二:高在BC延长线上
过点A作AE⊥BC交BC延长线于E,则AE=4。
同理,BE=3,EC=2,
此时BC=BE-EC=3-2=1,
周长=2(AB+BC)=2×(5+1)=12。
综上,□ABCD的周长为12或20。
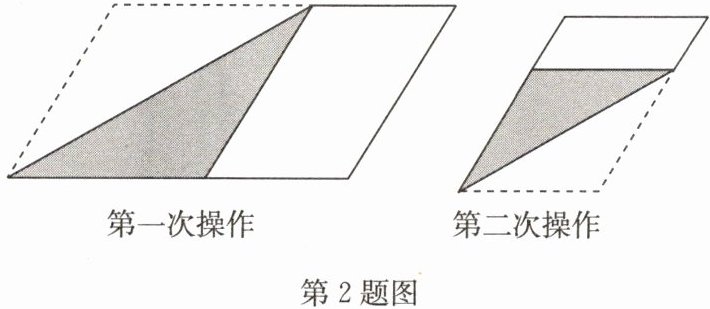
2. (2024·无锡天一实验中学期中)邻边长分别为$1$,$a(a > 1)$的平行四边形纸片,如图那样折一下,剪下一个边长等于$1$的菱形(称为第一次操作);再把剩下的平行四边形如图那样折一下,剪下一个边长等于此时平行四边形一边长的菱形(称为第二次操作);再把剩下的平行四边形如此反复操作下去. 若在第三次操作后,剩下的平行四边形为菱形,则$a$的值为
$\frac{5}{3}$或$\frac{4}{3}$或$\frac{5}{2}$或4
.
答案:
2. $\frac{5}{3}$或$\frac{4}{3}$或$\frac{5}{2}$或4
点拨:①如答图①,经历三次折叠后,四边形IJHF为菱形。
∵四边形ABCD为菱形,
∴$AB = AD = BC = CD = 1$,
∴$DF = CE = a - 1$。
∵四边形GCEH为菱形,
∴$GC = CE = a - 1$,
∴$DG = FH = 1 - (a - 1) = 2 - a$。
∵四边形DGJI为菱形,
∴$DI = DG = 2 - a$,
∴$IF = a - 1 - (2 - a) = 2a - 3$。
∵四边形IJHF为菱形,
∴$IF = HF$,即$2a - 3 = 2 - a$,解得$a = \frac{5}{3}$;

②如答图②,经历三次折叠后,四边形DIHF为菱形。
∵四边形ABCD为菱形,
∴$AB = AD = BC = CD = 1$,
∴$DF = CE = a - 1$。
∵四边形JCEG,IJGH,DIHF都为菱形,
∴$DI = \frac{1}{3}CD = \frac{1}{3}$,
∴$a - 1 = \frac{1}{3}$,
解得$a = \frac{4}{3}$;

③如答图③,经历三次折叠后,四边形FIJH为菱形。
∵四边形ABCD,DCEF为菱形,
∴$AB = AD = BC = CD = CE = DF = EF = 1$,
∴$FH = a - 2$。
∵四边形FIJH,IEGJ都为菱形,
∴$FH = FI = IE = \frac{1}{2}EF = \frac{1}{2}$,
∴$a - 2 = \frac{1}{2}$,
解得$a = \frac{5}{2}$;

④如答图④,经历三次折叠后,四边形HGIJ为菱形。
∵四边形ABCD,DCEF,FEGH,HGIJ都为菱形,
∴$AB = AD = DF = FH = 1$,
∴$HJ = a - 3$,
∴$HJ = IJ$,
∴$a - 3 = 1$,解得$a = 4$。

综上,$a$的值为$\frac{5}{3}$或$\frac{4}{3}$或$\frac{5}{2}$或4。
2. $\frac{5}{3}$或$\frac{4}{3}$或$\frac{5}{2}$或4
点拨:①如答图①,经历三次折叠后,四边形IJHF为菱形。
∵四边形ABCD为菱形,
∴$AB = AD = BC = CD = 1$,
∴$DF = CE = a - 1$。
∵四边形GCEH为菱形,
∴$GC = CE = a - 1$,
∴$DG = FH = 1 - (a - 1) = 2 - a$。
∵四边形DGJI为菱形,
∴$DI = DG = 2 - a$,
∴$IF = a - 1 - (2 - a) = 2a - 3$。
∵四边形IJHF为菱形,
∴$IF = HF$,即$2a - 3 = 2 - a$,解得$a = \frac{5}{3}$;

②如答图②,经历三次折叠后,四边形DIHF为菱形。
∵四边形ABCD为菱形,
∴$AB = AD = BC = CD = 1$,
∴$DF = CE = a - 1$。
∵四边形JCEG,IJGH,DIHF都为菱形,
∴$DI = \frac{1}{3}CD = \frac{1}{3}$,
∴$a - 1 = \frac{1}{3}$,
解得$a = \frac{4}{3}$;

③如答图③,经历三次折叠后,四边形FIJH为菱形。
∵四边形ABCD,DCEF为菱形,
∴$AB = AD = BC = CD = CE = DF = EF = 1$,
∴$FH = a - 2$。
∵四边形FIJH,IEGJ都为菱形,
∴$FH = FI = IE = \frac{1}{2}EF = \frac{1}{2}$,
∴$a - 2 = \frac{1}{2}$,
解得$a = \frac{5}{2}$;

④如答图④,经历三次折叠后,四边形HGIJ为菱形。
∵四边形ABCD,DCEF,FEGH,HGIJ都为菱形,
∴$AB = AD = DF = FH = 1$,
∴$HJ = a - 3$,
∴$HJ = IJ$,
∴$a - 3 = 1$,解得$a = 4$。

综上,$a$的值为$\frac{5}{3}$或$\frac{4}{3}$或$\frac{5}{2}$或4。
3. 如图,在$□ ABCD$中,$BD$为对角线,$EF$垂直平分$BD$,分别交$AD$,$BC$于点$E$,$F$,交$BD$于点$O$.
(1)求证:$BF = DE$;
(2)求证:$△ ABE≌△ CDF$;
(3)如果在$□ ABCD$中,$AB = 5$,$AD = 10$,有两动点$P$,$Q$分别从$B$,$D$两点同时出发,沿$△ BAE$和$△ DFC$各边运动一周,即点$P$自$B\rightarrow A\rightarrow E\rightarrow B$停止,点$Q$自$D\rightarrow F\rightarrow C\rightarrow D$停止,点$P$运动的路程是$m$,点$Q$运动的路程是$n$,当四边形$BPDQ$是平行四边形时,求$m$与$n$满足的数量关系.(画出示意图)

(1)求证:$BF = DE$;
(2)求证:$△ ABE≌△ CDF$;
(3)如果在$□ ABCD$中,$AB = 5$,$AD = 10$,有两动点$P$,$Q$分别从$B$,$D$两点同时出发,沿$△ BAE$和$△ DFC$各边运动一周,即点$P$自$B\rightarrow A\rightarrow E\rightarrow B$停止,点$Q$自$D\rightarrow F\rightarrow C\rightarrow D$停止,点$P$运动的路程是$m$,点$Q$运动的路程是$n$,当四边形$BPDQ$是平行四边形时,求$m$与$n$满足的数量关系.(画出示意图)

答案:
3. (1)证明:
∵四边形ABCD是平行四边形,
∴$AD // BC$,
∴$∠ ODE = ∠ OBF$。
∵EF垂直平分BD,
∴$OB = OD$。
在$△ OBF$和$△ ODE$中,$\begin{cases} ∠ OBF = ∠ ODE, \\ OB = OD, \\ ∠ BOF = ∠ DOE, \end{cases}$
∴$△ BOF ≌ △ DOE(ASA)$,
∴$BF = DE$。
(2)证明:
∵四边形ABCD是平行四边形,
∴$AB = CD$,$∠ A = ∠ C$,$AD = BC$。
∵$BF = DE$,
∴$AE = CF$。
在$△ ABE$和$△ CDF$中,$\begin{cases} AB = CD, \\ ∠ A = ∠ C, \\ AE = CF, \end{cases}$
∴$△ ABE ≌ △ CDF(SAS)$。
(3)解:
∵EF垂直平分BD,
∴$BF = DF$。
∵$△ ABE ≌ △ CDF$,
∴$BE = DF$,
∴$△ ABE$的周长是$BE + AE + AB = DE + AE + AB = AD + AB = 15$,$△ DFC$的周长也是15,分以下3种情况讨论:
①当点P在AB上,点Q在CD上时,如答图①。
∵$AB // CD$,
∴$∠ BPO = ∠ DQO$。
∵$∠ BOP = ∠ DOQ$,$OB = OD$,
∴$△ BPO ≌ △ DQO$,
∴$BP = DQ$,
∴$m + n = BP + DF + CF + CQ = DF + CF + CQ + DQ = DF + CF + CD = 15$;

②当点P在AE上,点Q在CF上时,如答图②。
∵$AD // BC$,
∴$∠ PEO = ∠ QFO$。
∵$△ EOD ≌ △ FOB$,
∴$OE = OF$。
又
∵$∠ EOP = ∠ FOQ$,
∴$△ PEO ≌ △ QFO$,
∴$PE = QF$。
∵$AE = CF$,
∴$CQ = AP$,
∴$m + n = AB + AP + DF + FQ = CD + CQ + DF + FQ = DF + CF + CD = 15$;
③当点P在BE上,点Q在DF上时,如答图③。
∵$DE = BF$,$DE // BF$,
∴四边形BEDF是平行四边形,
∴$OE = OF$,$BE // DF$,
∴$∠ PEO = ∠ QFO$。
∵$∠ EOP = ∠ FOQ$,
∴$△ PEO ≌ △ QFO$,
∴$PE = FQ$,
∴$m + n = AB + AE + PE + DQ = CD + CF + QF + DQ = DF + CF + CD = 15$。
综上,$m$与$n$的关系为$m + n = 15$。
3. (1)证明:
∵四边形ABCD是平行四边形,
∴$AD // BC$,
∴$∠ ODE = ∠ OBF$。
∵EF垂直平分BD,
∴$OB = OD$。
在$△ OBF$和$△ ODE$中,$\begin{cases} ∠ OBF = ∠ ODE, \\ OB = OD, \\ ∠ BOF = ∠ DOE, \end{cases}$
∴$△ BOF ≌ △ DOE(ASA)$,
∴$BF = DE$。
(2)证明:
∵四边形ABCD是平行四边形,
∴$AB = CD$,$∠ A = ∠ C$,$AD = BC$。
∵$BF = DE$,
∴$AE = CF$。
在$△ ABE$和$△ CDF$中,$\begin{cases} AB = CD, \\ ∠ A = ∠ C, \\ AE = CF, \end{cases}$
∴$△ ABE ≌ △ CDF(SAS)$。
(3)解:
∵EF垂直平分BD,
∴$BF = DF$。
∵$△ ABE ≌ △ CDF$,
∴$BE = DF$,
∴$△ ABE$的周长是$BE + AE + AB = DE + AE + AB = AD + AB = 15$,$△ DFC$的周长也是15,分以下3种情况讨论:
①当点P在AB上,点Q在CD上时,如答图①。
∵$AB // CD$,
∴$∠ BPO = ∠ DQO$。
∵$∠ BOP = ∠ DOQ$,$OB = OD$,
∴$△ BPO ≌ △ DQO$,
∴$BP = DQ$,
∴$m + n = BP + DF + CF + CQ = DF + CF + CQ + DQ = DF + CF + CD = 15$;

②当点P在AE上,点Q在CF上时,如答图②。
∵$AD // BC$,
∴$∠ PEO = ∠ QFO$。
∵$△ EOD ≌ △ FOB$,
∴$OE = OF$。
又
∵$∠ EOP = ∠ FOQ$,
∴$△ PEO ≌ △ QFO$,
∴$PE = QF$。
∵$AE = CF$,
∴$CQ = AP$,
∴$m + n = AB + AP + DF + FQ = CD + CQ + DF + FQ = DF + CF + CD = 15$;
③当点P在BE上,点Q在DF上时,如答图③。
∵$DE = BF$,$DE // BF$,
∴四边形BEDF是平行四边形,
∴$OE = OF$,$BE // DF$,
∴$∠ PEO = ∠ QFO$。
∵$∠ EOP = ∠ FOQ$,
∴$△ PEO ≌ △ QFO$,
∴$PE = FQ$,
∴$m + n = AB + AE + PE + DQ = CD + CF + QF + DQ = DF + CF + CD = 15$。
综上,$m$与$n$的关系为$m + n = 15$。