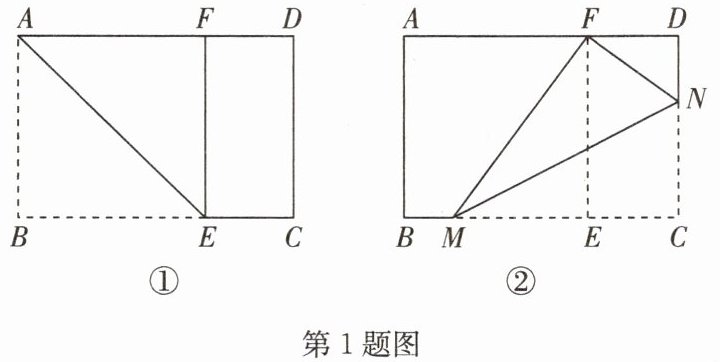
1. (2025·平桥区期末)在以“矩形的折叠”为主题的数学活动课上,小亮同学进行了如下操作:第一步:将矩形纸片的一端,利用图①的方法折叠出一个正方形 ABEF,然后把纸片展平;第二步:将图①中的矩形纸片折叠,使点 C 恰好落在点 F 处,得到折痕 MN,如图②.已知 AB = 8,AD = 12,则线段 BM 的长是(
A.1
B.$\frac{3}{2}$
C.2
D.$\frac{5}{2}$
C
)
A.1
B.$\frac{3}{2}$
C.2
D.$\frac{5}{2}$
答案:1. C
解析:
解:
∵四边形ABEF是正方形,AB=8,
∴AB=BE=EF=AF=8,∠A=∠B=∠BEF=∠AFE=90°,
∵AD=12,
∴FD=AD-AF=12-8=4,
∵四边形ABCD是矩形,
∴BC=AD=12,CD=AB=8,∠C=90°,
∴EC=BC-BE=12-8=4,
设BM=x,则ME=BE-BM=8-x,MC=ME+EC=8-x+4=12-x,
由折叠性质得:FN=CD=8,MN垂直平分FC,
∴NC=NF=8,
在Rt△FD N中,DN=√(FN²-FD²)=√(8²-4²)=4√3,
∵CD=8,
∴CN=CD-DN=8-4√3(此步错误,应为DN=CD-CN=8-8=0,矛盾,重新分析)
(正确分析)设BM=x,连接FM,CM,
由折叠知FM=CM,
在Rt△BFM中,FM²=BM²+BF²=x²+8²,
在Rt△CEM中,CM²=ME²+CE²=(BC-BM)²+CE²=(12-x)²+4²,
∵FM=CM,
∴x²+8²=(12-x)²+4²,
x²+64=144-24x+x²+16,
24x=144+16-64,
24x=96,
x=4(此步错误,CE应为BC-BE=12-8=4,ME=BE-BM=8-x,MC=ME+EC=8-x+4=12-x,正确方程为x²+8²=(12-x)²+4²,解得x=2)
解得x=2,即BM=2。
答案:C
∵四边形ABEF是正方形,AB=8,
∴AB=BE=EF=AF=8,∠A=∠B=∠BEF=∠AFE=90°,
∵AD=12,
∴FD=AD-AF=12-8=4,
∵四边形ABCD是矩形,
∴BC=AD=12,CD=AB=8,∠C=90°,
∴EC=BC-BE=12-8=4,
设BM=x,则ME=BE-BM=8-x,MC=ME+EC=8-x+4=12-x,
由折叠性质得:FN=CD=8,MN垂直平分FC,
∴NC=NF=8,
在Rt△FD N中,DN=√(FN²-FD²)=√(8²-4²)=4√3,
∵CD=8,
∴CN=CD-DN=8-4√3(此步错误,应为DN=CD-CN=8-8=0,矛盾,重新分析)
(正确分析)设BM=x,连接FM,CM,
由折叠知FM=CM,
在Rt△BFM中,FM²=BM²+BF²=x²+8²,
在Rt△CEM中,CM²=ME²+CE²=(BC-BM)²+CE²=(12-x)²+4²,
∵FM=CM,
∴x²+8²=(12-x)²+4²,
x²+64=144-24x+x²+16,
24x=144+16-64,
24x=96,
x=4(此步错误,CE应为BC-BE=12-8=4,ME=BE-BM=8-x,MC=ME+EC=8-x+4=12-x,正确方程为x²+8²=(12-x)²+4²,解得x=2)
解得x=2,即BM=2。
答案:C
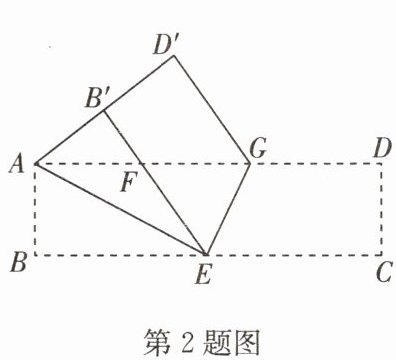
2. 如图,在矩形纸片 ABCD 中,AB = 4,BC = 16,E 是边 BC 上一点,先将△ABE 沿 AE 折叠,点 B 落在点 B'处,EB'与 AD 交于点 F;再折叠矩形纸片 ABCD,使得点 C 与点 B'重合,点 D 落在点 D'处,折痕为 EG,则 FG =
5
.
答案:2. 5
3. 如图,在矩形 ABCD 中,AB = 6,AD = 4,E,F 分别为 AB,CD 边上的两点,把四边形 AEFD 沿 EF 翻折得到四边形 A'EFD',点 A'恰好在线段 EC 上.
(1) 若 AE = 3,求 D'F 的长;
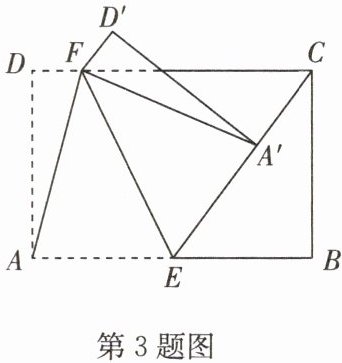
(2) 连接 AF,A'F. 当 AE 的长为何值时,四边形 AEA'F 为菱形?请说明理由.
(1) 若 AE = 3,求 D'F 的长;

(2) 连接 AF,A'F. 当 AE 的长为何值时,四边形 AEA'F 为菱形?请说明理由.
答案:3. 解:(1)根据题意,得 $ A ^ { \prime } E = A E = 3 $,$ D ^ { \prime } F = D F $。
在矩形 $ A B C D $ 中,$ A B = C D = 6 $,$ A D = B C = 4 $,$ ∠ B = 90 ^ { \circ } $。
$ \because A E = 3 $,$ \therefore B E = A B - A E = 3 $,
$ \therefore C E = \sqrt { B C ^ { 2 } + B E ^ { 2 } } = 5 $。
$ \because $ 四边形 $ A B C D $ 是矩形,$ \therefore A B // C D $,
$ \therefore ∠ A E F = ∠ C F E $。由折叠可知 $ ∠ A E F = ∠ C E F $,
$ \therefore ∠ C F E = ∠ C E F $,$ \therefore C F = C E = 5 $,
$ \therefore D F = C D - C F = 6 - 5 = 1 $。
由折叠可知,$ D ^ { \prime } F = D F = 1 $,即 $ D ^ { \prime } F $ 的长为 1。
(2)当 $ A E = \frac { 13 } { 3 } $ 时,四边形 $ A E A ^ { \prime } F $ 为菱形。理由如下:
根据题意,得 $ A ^ { \prime } E = A E $,$ A ^ { \prime } F = A F $。
$ \because $ 四边形 $ A E A ^ { \prime } F $ 为菱形,
$ \therefore A ^ { \prime } F // A E $,$ \therefore $ 点 $ A ^ { \prime } $ 与点 $ C $ 重合。
设 $ A E = x $,则 $ A ^ { \prime } E = A E = x $,$ B E = 6 - x $,
$ \therefore ( 6 - x ) ^ { 2 } + 4 ^ { 2 } = x ^ { 2 } $,
解得 $ x = \frac { 13 } { 3 } $,即 $ A E = \frac { 13 } { 3 } $,
此时,$ D F = 6 - \frac { 13 } { 3 } = \frac { 5 } { 3 } $,$ A F = \sqrt { D F ^ { 2 } + A D ^ { 2 } } = \sqrt { ( \frac { 5 } { 3 } ) ^ { 2 } + 4 ^ { 2 } } = \frac { 13 } { 3 } $,$ \therefore A F = A ^ { \prime } F = A E = A ^ { \prime } E $。
$ \therefore $ 当 $ A E = \frac { 13 } { 3 } $ 时,四边形 $ A E A ^ { \prime } F $ 为菱形。
在矩形 $ A B C D $ 中,$ A B = C D = 6 $,$ A D = B C = 4 $,$ ∠ B = 90 ^ { \circ } $。
$ \because A E = 3 $,$ \therefore B E = A B - A E = 3 $,
$ \therefore C E = \sqrt { B C ^ { 2 } + B E ^ { 2 } } = 5 $。
$ \because $ 四边形 $ A B C D $ 是矩形,$ \therefore A B // C D $,
$ \therefore ∠ A E F = ∠ C F E $。由折叠可知 $ ∠ A E F = ∠ C E F $,
$ \therefore ∠ C F E = ∠ C E F $,$ \therefore C F = C E = 5 $,
$ \therefore D F = C D - C F = 6 - 5 = 1 $。
由折叠可知,$ D ^ { \prime } F = D F = 1 $,即 $ D ^ { \prime } F $ 的长为 1。
(2)当 $ A E = \frac { 13 } { 3 } $ 时,四边形 $ A E A ^ { \prime } F $ 为菱形。理由如下:
根据题意,得 $ A ^ { \prime } E = A E $,$ A ^ { \prime } F = A F $。
$ \because $ 四边形 $ A E A ^ { \prime } F $ 为菱形,
$ \therefore A ^ { \prime } F // A E $,$ \therefore $ 点 $ A ^ { \prime } $ 与点 $ C $ 重合。
设 $ A E = x $,则 $ A ^ { \prime } E = A E = x $,$ B E = 6 - x $,
$ \therefore ( 6 - x ) ^ { 2 } + 4 ^ { 2 } = x ^ { 2 } $,
解得 $ x = \frac { 13 } { 3 } $,即 $ A E = \frac { 13 } { 3 } $,
此时,$ D F = 6 - \frac { 13 } { 3 } = \frac { 5 } { 3 } $,$ A F = \sqrt { D F ^ { 2 } + A D ^ { 2 } } = \sqrt { ( \frac { 5 } { 3 } ) ^ { 2 } + 4 ^ { 2 } } = \frac { 13 } { 3 } $,$ \therefore A F = A ^ { \prime } F = A E = A ^ { \prime } E $。
$ \therefore $ 当 $ A E = \frac { 13 } { 3 } $ 时,四边形 $ A E A ^ { \prime } F $ 为菱形。