22. (8 分)(2024·泰州中学月考)如图,在四边形 $ABCD$ 中,$AD// BC$,$BC⊥ CD$,$AD = 8\ \mathrm{cm}$,$BC = 12\ \mathrm{cm}$,点 $E$ 从点 $A$ 出发以 $1\ \mathrm{cm/s}$ 的速度向点 $D$ 运动,同时,点 $F$ 从点 $B$ 出发,以 $2\ \mathrm{cm/s}$ 的速度向点 $C$ 运动,设运动时间为 $t\ \mathrm{s}$.
(1)$t$ 取何值时,四边形 $EFCD$ 为矩形?
(2)$M$ 是线段 $BC$ 上一点,且 $BM = 5\ \mathrm{cm}$,$t$ 取何值时,以 $A$,$M$,$E$,$F$ 为顶点的四边形是平行四边形?
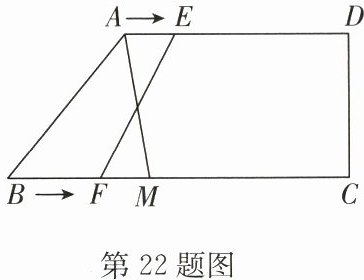
(1)$t$ 取何值时,四边形 $EFCD$ 为矩形?
(2)$M$ 是线段 $BC$ 上一点,且 $BM = 5\ \mathrm{cm}$,$t$ 取何值时,以 $A$,$M$,$E$,$F$ 为顶点的四边形是平行四边形?

答案:22.解:(1)当DE=CF时,四边形EFCD为矩形,则有8−t=12−2t,解得t=4,
∴当t=4时,四边形EFCD为矩形.
(2)①当点F在线段BM上,AE=FM时,以A,M,E,F 为顶点的四边形是平行四边形,则有t=5−2t,
解得t=$\frac{5}{3}$;
②当点F在线段CM上,AE=FM时,以A,M,E,F为顶点的四边形是平行四边形,则有t=2t−5,
解得t=5.
综上所述,当t的值为$\frac{5}{3}$或5时,以A,M,E,F为顶点的四边形是平行四边形.
∴当t=4时,四边形EFCD为矩形.
(2)①当点F在线段BM上,AE=FM时,以A,M,E,F 为顶点的四边形是平行四边形,则有t=5−2t,
解得t=$\frac{5}{3}$;
②当点F在线段CM上,AE=FM时,以A,M,E,F为顶点的四边形是平行四边形,则有t=2t−5,
解得t=5.
综上所述,当t的值为$\frac{5}{3}$或5时,以A,M,E,F为顶点的四边形是平行四边形.
23. (12 分)如图,在 $△ ABC$ 中,$∠ ACB = 90^{\circ}$,$BC$ 的垂直平分线 $DE$ 交 $BC$ 于点 $D$,交 $AB$ 于点 $E$,点 $F$ 在 $DE$ 的延长线上,且 $AF = CE$.
(1)四边形 $ACEF$ 是平行四边形吗?说明理由.
(2)当 $∠ B$ 的大小满足什么条件时,四边形 $ACEF$ 为菱形?说明理由.
(3)四边形 $ACEF$ 有可能是正方形吗?为什么?
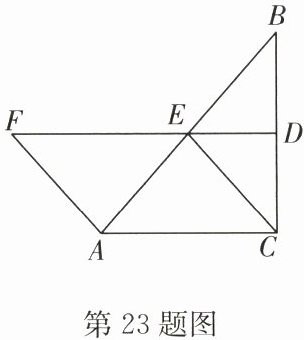
(1)四边形 $ACEF$ 是平行四边形吗?说明理由.
(2)当 $∠ B$ 的大小满足什么条件时,四边形 $ACEF$ 为菱形?说明理由.
(3)四边形 $ACEF$ 有可能是正方形吗?为什么?

答案:23.解:(1)四边形ACEF是平行四边形.理由如下:
∵DE垂直平分BC,
∴D为BC的中点,ED⊥BC;
又
∵∠ACB=90°,
∴AC⊥BC,
∴ED//AC,
∴∠AEF=∠EAC,ED是△ABC的中位线,
∴E为AB的中点,
∴在Rt△ABC中,CE是斜边AB的中线,
∴CE=AE=AF,
∴∠F=∠AEF=∠EAC=∠ACE,
∴∠FAE=∠AEC,
∴AF//EC,
∴四边形ACEF是平行四边形.
(2)当∠B=30°时,四边形ACEF为菱形.理由如下:
∵∠ACB=90°,∠B=30°,
∴AC=$\frac{1}{2}$AB.
由(1)可知CE=$\frac{1}{2}$AB,
∴AC=CE;
又
∵四边形ACEF为平行四边形,
∴四边形ACEF为菱形.
(3)四边形ACEF不可能是正方形.理由如下:
∵∠ACB=90°,∠ACE<∠ACB,
∴∠ACE<90°,不能为直角,
∴四边形ACEF不可能是正方形.
∵DE垂直平分BC,
∴D为BC的中点,ED⊥BC;
又
∵∠ACB=90°,
∴AC⊥BC,
∴ED//AC,
∴∠AEF=∠EAC,ED是△ABC的中位线,
∴E为AB的中点,
∴在Rt△ABC中,CE是斜边AB的中线,
∴CE=AE=AF,
∴∠F=∠AEF=∠EAC=∠ACE,
∴∠FAE=∠AEC,
∴AF//EC,
∴四边形ACEF是平行四边形.
(2)当∠B=30°时,四边形ACEF为菱形.理由如下:
∵∠ACB=90°,∠B=30°,
∴AC=$\frac{1}{2}$AB.
由(1)可知CE=$\frac{1}{2}$AB,
∴AC=CE;
又
∵四边形ACEF为平行四边形,
∴四边形ACEF为菱形.
(3)四边形ACEF不可能是正方形.理由如下:
∵∠ACB=90°,∠ACE<∠ACB,
∴∠ACE<90°,不能为直角,
∴四边形ACEF不可能是正方形.
24. (12 分)如图①,在矩形纸片 $ABCD$ 中,$AB = 3\ \mathrm{cm}$,$AD = 5\ \mathrm{cm}$,折叠纸片使点 $B$ 落在边 $AD$ 上的点 $E$ 处,折痕为 $PQ$,过点 $E$ 作 $EF// AB$,交 $PQ$ 于点 $F$,连接 $BF$.
(1)求证:四边形 $BFEP$ 为菱形.
(2)当点 $E$ 在 $AD$ 边上移动时,折痕的端点 $P$,$Q$ 也随之移动.
①如图②,当点 $Q$ 与点 $C$ 重合时,求菱形 $BFEP$ 的边长;
②若限定点 $P$,$Q$ 分别在边 $BA$,$BC$ 上移动,求出点 $E$ 在边 $AD$ 上移动的最大距离.
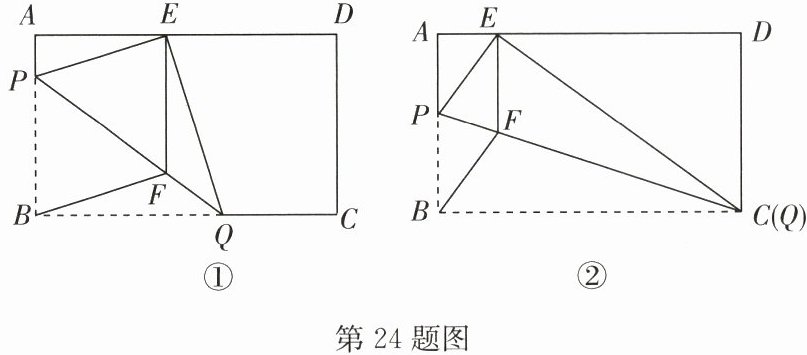
(1)求证:四边形 $BFEP$ 为菱形.
(2)当点 $E$ 在 $AD$ 边上移动时,折痕的端点 $P$,$Q$ 也随之移动.
①如图②,当点 $Q$ 与点 $C$ 重合时,求菱形 $BFEP$ 的边长;
②若限定点 $P$,$Q$ 分别在边 $BA$,$BC$ 上移动,求出点 $E$ 在边 $AD$ 上移动的最大距离.

答案:24.(1)证明:
∵折叠纸片使点B落在边AD上的点E处,折痕为PQ,
∴点B与点E关于PQ对称,
∴PB=PE,BF=EF,∠BPF=∠EPF;
又
∵EF//AB,
∴∠BPF=∠EFP,
∴∠EPF=∠EFP,
∴EP=EF,
∴BP=BF=EF=EP,
∴四边形BFEP为菱形.
(2)解:①
∵四边形ABCD是矩形,
∴BC=AD=5cm,CD=AB=3cm,∠A=∠D=90°.
∵点B与点E关于PQ对称,
∴PB=PE,CE=BC=5cm.
在Rt△CDE中,
DE=$\sqrt{CE^2-CD^2}=\sqrt{5^2-3^2}=4$(cm),
∴AE=AD−DE=5−4=1(cm),
在Rt△APE中,AE=1cm,AP=3−PB=3−PE,
∴EP²=1²+(3−EP)²,解得EP=$\frac{5}{3}$cm,
∴菱形BFEP的边长为$\frac{5}{3}$cm.
②当点Q与点C重合时,点E离点A最近,
由①知,此时AE=1cm.
当点P与点A重合时,点E离点A最远,
此时四边形ABQE为正方形,AE=AB=3cm,
∴点E在边AD上移动的最大距离为2cm
∵折叠纸片使点B落在边AD上的点E处,折痕为PQ,
∴点B与点E关于PQ对称,
∴PB=PE,BF=EF,∠BPF=∠EPF;
又
∵EF//AB,
∴∠BPF=∠EFP,
∴∠EPF=∠EFP,
∴EP=EF,
∴BP=BF=EF=EP,
∴四边形BFEP为菱形.
(2)解:①
∵四边形ABCD是矩形,
∴BC=AD=5cm,CD=AB=3cm,∠A=∠D=90°.
∵点B与点E关于PQ对称,
∴PB=PE,CE=BC=5cm.
在Rt△CDE中,
DE=$\sqrt{CE^2-CD^2}=\sqrt{5^2-3^2}=4$(cm),
∴AE=AD−DE=5−4=1(cm),
在Rt△APE中,AE=1cm,AP=3−PB=3−PE,
∴EP²=1²+(3−EP)²,解得EP=$\frac{5}{3}$cm,
∴菱形BFEP的边长为$\frac{5}{3}$cm.
②当点Q与点C重合时,点E离点A最近,
由①知,此时AE=1cm.
当点P与点A重合时,点E离点A最远,
此时四边形ABQE为正方形,AE=AB=3cm,
∴点E在边AD上移动的最大距离为2cm