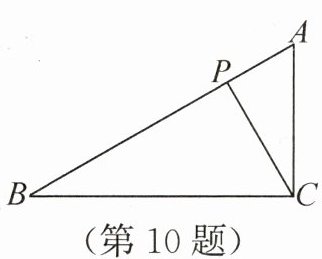
10. 如图,已知$\triangle ACP \backsim \triangle ABC$. 若$AC = 4$,$AP = 2$,则$AB =$
8
.
答案:10.8
解析:
解:因为$\triangle ACP \backsim \triangle ABC$,所以$\frac{AC}{AB}=\frac{AP}{AC}$。
已知$AC = 4$,$AP = 2$,代入可得$\frac{4}{AB}=\frac{2}{4}$,解得$AB = 8$。
8
已知$AC = 4$,$AP = 2$,代入可得$\frac{4}{AB}=\frac{2}{4}$,解得$AB = 8$。
8
11. 以正方形各边的中点为顶点,可以得到一个新正方形,则新正方形与原正方形的相似比为
$\sqrt{2}:2$
.答案:11.$\sqrt{2}:2$
解析:
设原正方形的边长为$a$,则原正方形各边中点之间的距离为$\sqrt{(\frac{a}{2})^2 + (\frac{a}{2})^2} = \frac{\sqrt{2}}{2}a$,即新正方形的边长为$\frac{\sqrt{2}}{2}a$。新正方形与原正方形的相似比为$\frac{\sqrt{2}}{2}a : a = \sqrt{2}:2$。
$\sqrt{2}:2$
$\sqrt{2}:2$
12. 如图,把矩形$ABCD$对折,折痕为$MN$,矩形$DMNC$与矩形$ABCD$相似. 已知$AB = 4$,则$AD$的长为

$4\sqrt{2}$
.
答案:12.$4\sqrt{2}$ 解析:因为矩形$DMNC$与矩形$ABCD$相似,所以$\frac{DM}{DC}=\frac{AB}{AD}$.因为$DM=\frac{1}{2}AD,DC=AB$,所以$\frac{1}{2}AD^2=AB^2$,所以$AD=\sqrt{2}AB$.因为$AB=4$,所以$AD=4\sqrt{2}$.
解析:
解:
∵矩形$DMNC$与矩形$ABCD$相似,
∴$\frac{DM}{DC}=\frac{AB}{AD}$。
∵$M$为$AD$中点,$DC = AB$,
∴$DM=\frac{1}{2}AD$,$DC = AB = 4$。
∴$\frac{\frac{1}{2}AD}{4}=\frac{4}{AD}$,
即$\frac{1}{2}AD^2=16$,$AD^2 = 32$,
解得$AD = 4\sqrt{2}$(负值舍去)。
故$AD$的长为$4\sqrt{2}$。
∵矩形$DMNC$与矩形$ABCD$相似,
∴$\frac{DM}{DC}=\frac{AB}{AD}$。
∵$M$为$AD$中点,$DC = AB$,
∴$DM=\frac{1}{2}AD$,$DC = AB = 4$。
∴$\frac{\frac{1}{2}AD}{4}=\frac{4}{AD}$,
即$\frac{1}{2}AD^2=16$,$AD^2 = 32$,
解得$AD = 4\sqrt{2}$(负值舍去)。
故$AD$的长为$4\sqrt{2}$。
13. 新素养 推理能力 如图,在$□ ABCD$中,$AC$与$BD$交于点$O$,$F$,$E$,$M$,$N$分别为$AO$,$BO$,$CO$,$DO$的中点,这样形成一个$□ FEMN$,求证:$□ FEMN \backsim □ ABCD$.


答案:13.因为$F,E,M,N$分别为$AO,BO,CO,DO$的中点,所以$FE,EM,MN,NF$分别为$\triangle AOB,\triangle BOC,\triangle COD,\triangle DOA$的中位线,所以$FE=\frac{1}{2}AB,EM=\frac{1}{2}BC,MN=\frac{1}{2}CD,NF=\frac{1}{2}DA$,$FE // AB,EM // BC,MN // CD,NF // DA$,所以$\frac{FE}{AB}=\frac{EM}{BC}=\frac{MN}{CD}=\frac{NF}{DA},\angle OFE=\angle OAB,\angle OEF=\angle OBA,\angle OEM=\angle OBC,\angle OMN=\angle OCD,\angle ONM=\angle ODC,\angle ONF=\angle ODA,\angle OFN=\angle OAD$,所以$\angle EFN=\angle BAD,\angle FEM=\angle ABC,\angle EMN=\angle BCD,\angle MNF=\angle CDA$,所以$□ FEMN ∼ □ ABCD$.
14. 新素养 应用意识 把标准纸一次又一次对开,可以得到均相似的“开纸”. 现在我们在长为 $2\sqrt{2}$,宽为 1 的矩形纸片中画两个小矩形,使这两个小矩形的每条边都与原矩形纸的边平行,或小矩形的边在原矩形纸的边上,且每个小矩形均与原矩形纸相似,然后将它们剪下,则所剪得的两个小矩形纸片周长之和的最大值为(
A.$4\sqrt{2}$
B.$4\sqrt{6}$
C.$4\sqrt{2} + \dfrac{15}{4}$
D.$4\sqrt{6} + \dfrac{15}{4}$
C
)A.$4\sqrt{2}$
B.$4\sqrt{6}$
C.$4\sqrt{2} + \dfrac{15}{4}$
D.$4\sqrt{6} + \dfrac{15}{4}$
答案:14.C 解析:根据题意,使两个矩形的长、宽之和最大,且两个矩形的长、宽之比均为$2\sqrt{2}:1$,则其中一个矩形的长为$1$,宽为$1 × \frac{1}{2\sqrt{2}}=\frac{\sqrt{2}}{4}$,所以另一个矩形的长为$2\sqrt{2}-\frac{\sqrt{2}}{4}=\frac{7\sqrt{2}}{4}$,宽为$\frac{7\sqrt{2}}{4} × \frac{1}{2\sqrt{2}}=\frac{7}{8}$,所以所剪得的两个小矩形纸片周长之和的最大值为$2 × (1+\frac{\sqrt{2}}{4}+\frac{7\sqrt{2}}{4}+\frac{7}{8})=4\sqrt{2}+\frac{15}{4}$.
15. 如图,已知矩形$ABCD$的长$AB = 30$,宽$BC = 20$. 若矩形$ABCD$与矩形$A'B'C'D'$相似,则$x$的值是

1.5或9
.
答案:15.1.5或9 解析:因为$AB=30,BC=20$,所以分类讨论如下:①若矩形$A'B'C'D' ∼$矩形$ABCD$,则$\frac{A'B'}{AB}=\frac{B'C'}{BC}$,即$\frac{30-2x}{30}=\frac{20-2}{20}$,解得$x=1.5$;②若矩形$B'C'D'A' ∼$矩形$ABCD$,则$\frac{B'C'}{AB}=\frac{C'D'}{BC}$,即$\frac{20-2x}{30}=\frac{30-2x}{20}$,解得$x=9$.综上所述,$x$的值是1.5或9.
解析:
解:已知矩形$ABCD$中,$AB = 30$,$BC = 20$,则矩形$A'B'C'D'$的长为$30 - 2x$,宽为$20 - 2$。
①若矩形$A'B'C'D' ∼$矩形$ABCD$,则$\frac{A'B'}{AB}=\frac{B'C'}{BC}$,即$\frac{30 - 2x}{30}=\frac{20 - 2}{20}$,解得$x = 1.5$;
②若矩形$B'C'D'A' ∼$矩形$ABCD$,则$\frac{B'C'}{AB}=\frac{C'D'}{BC}$,即$\frac{20 - 2x}{30}=\frac{30 - 2x}{20}$,解得$x = 9$。
综上,$x$的值是$1.5$或$9$。
①若矩形$A'B'C'D' ∼$矩形$ABCD$,则$\frac{A'B'}{AB}=\frac{B'C'}{BC}$,即$\frac{30 - 2x}{30}=\frac{20 - 2}{20}$,解得$x = 1.5$;
②若矩形$B'C'D'A' ∼$矩形$ABCD$,则$\frac{B'C'}{AB}=\frac{C'D'}{BC}$,即$\frac{20 - 2x}{30}=\frac{30 - 2x}{20}$,解得$x = 9$。
综上,$x$的值是$1.5$或$9$。
16. (2025·四川眉山)如图,在平面直角坐标系中,用 12 个以原点$O$为公共顶点的相似三角形组成形如海螺的图案. 若$OA = 1$,$\angle OAB = 90°$,则点$G$的坐标为

$(-\frac{64}{27},0)$
.
答案:16.$(-\frac{64}{27},0)$ 解析:因为12个直角三角形相似,所以$\angle AOB=\frac{1}{12} × 360°=30°$.因为$\angle OAB=90°$,所以$AB=\frac{1}{2}OB$,所以$OA=\sqrt{OB^2-AB^2}=\frac{\sqrt{3}}{2}OB$,所以$OB=\frac{2\sqrt{3}}{3}OA$.同理可得$OC=\frac{2\sqrt{3}}{3}OB=(\frac{2\sqrt{3}}{3})^2OA,OD=\frac{2\sqrt{3}}{3}OC=(\frac{2\sqrt{3}}{3})^3OA$,$···$,$OG=\frac{2\sqrt{3}}{3}OF=(\frac{2\sqrt{3}}{3})^6OA=\frac{64}{27}OA$.因为$OA=1$,所以$OG=\frac{64}{27}$.因为点$G$在$x$轴负半轴上,所以点$G$的坐标为$(-\frac{64}{27},0)$.
解析:
解:因为12个直角三角形相似,所以$\angle AOB = \frac{1}{12} × 360° = 30°$。
因为$\angle OAB = 90°$,所以$AB = \frac{1}{2}OB$,则$OA = \sqrt{OB^2 - AB^2} = \frac{\sqrt{3}}{2}OB$,故$OB = \frac{2\sqrt{3}}{3}OA$。
同理可得:$OC = \frac{2\sqrt{3}}{3}OB = (\frac{2\sqrt{3}}{3})^2 OA$,$OD = (\frac{2\sqrt{3}}{3})^3 OA$,$···$,$OG = (\frac{2\sqrt{3}}{3})^6 OA$。
计算$(\frac{2\sqrt{3}}{3})^6 = (\frac{(2\sqrt{3})^2}{3^2})^3 = (\frac{12}{9})^3 = (\frac{4}{3})^3 = \frac{64}{27}$,所以$OG = \frac{64}{27}OA$。
因为$OA = 1$,所以$OG = \frac{64}{27}$。
又因为点$G$在$x$轴负半轴上,所以点$G$的坐标为$(-\frac{64}{27}, 0)$。
$(-\frac{64}{27},0)$
因为$\angle OAB = 90°$,所以$AB = \frac{1}{2}OB$,则$OA = \sqrt{OB^2 - AB^2} = \frac{\sqrt{3}}{2}OB$,故$OB = \frac{2\sqrt{3}}{3}OA$。
同理可得:$OC = \frac{2\sqrt{3}}{3}OB = (\frac{2\sqrt{3}}{3})^2 OA$,$OD = (\frac{2\sqrt{3}}{3})^3 OA$,$···$,$OG = (\frac{2\sqrt{3}}{3})^6 OA$。
计算$(\frac{2\sqrt{3}}{3})^6 = (\frac{(2\sqrt{3})^2}{3^2})^3 = (\frac{12}{9})^3 = (\frac{4}{3})^3 = \frac{64}{27}$,所以$OG = \frac{64}{27}OA$。
因为$OA = 1$,所以$OG = \frac{64}{27}$。
又因为点$G$在$x$轴负半轴上,所以点$G$的坐标为$(-\frac{64}{27}, 0)$。
$(-\frac{64}{27},0)$
17. (2025·江苏镇江模拟)如图,$An$系列矩形纸张的规格特征如下:① 各矩形纸张都相似;② A1 纸对裁后可以得到两张 A2 纸,A2 纸对裁后可以得到两张 A3 纸,…,$An$纸对裁后可以得到两张 $A(n + 1)$ 纸.
(1)A1 纸的面积是 A2 纸面积的
(2)根据 $An$ 系列纸张的规格特征,求出该系列纸张的长与宽(长大于宽)之比;
(3)设一张 A1 纸的质量为 $a\ \mathrm{g}$,试求出一张 A8 纸的质量.(用含 $a$ 的代数式表示)

(1)A1 纸的面积是 A2 纸面积的
2
倍,A2 纸的周长是 A4 纸周长的2
倍;(2)根据 $An$ 系列纸张的规格特征,求出该系列纸张的长与宽(长大于宽)之比;
(3)设一张 A1 纸的质量为 $a\ \mathrm{g}$,试求出一张 A8 纸的质量.(用含 $a$ 的代数式表示)

答案:17.(1)2 2
(2)设A1纸的长和宽分别为$m,n$,则A2纸的长和宽分别为$n,\frac{1}{2}m$,则有$\frac{m}{n}=\frac{n}{\frac{1}{2}m}$,所以$\frac{m}{n}=\sqrt{2}$,即该系列纸张的长与宽之比为$\sqrt{2}:1$.
(3)因为一张A1纸的质量为$a$g,A2纸的面积是A1纸面积的一半,所以一张A2纸的质量为$\frac{1}{2}a$g.同理,一张A3纸的质量为$(\frac{1}{2})^2a$g,$···$,一张An纸的质量为$(\frac{1}{2})^{n-1}a$g,所以一张A8纸的质量为$(\frac{1}{2})^{8-1}a=(\frac{1}{2})^7a=\frac{a}{128}(g)$.
(2)设A1纸的长和宽分别为$m,n$,则A2纸的长和宽分别为$n,\frac{1}{2}m$,则有$\frac{m}{n}=\frac{n}{\frac{1}{2}m}$,所以$\frac{m}{n}=\sqrt{2}$,即该系列纸张的长与宽之比为$\sqrt{2}:1$.
(3)因为一张A1纸的质量为$a$g,A2纸的面积是A1纸面积的一半,所以一张A2纸的质量为$\frac{1}{2}a$g.同理,一张A3纸的质量为$(\frac{1}{2})^2a$g,$···$,一张An纸的质量为$(\frac{1}{2})^{n-1}a$g,所以一张A8纸的质量为$(\frac{1}{2})^{8-1}a=(\frac{1}{2})^7a=\frac{a}{128}(g)$.