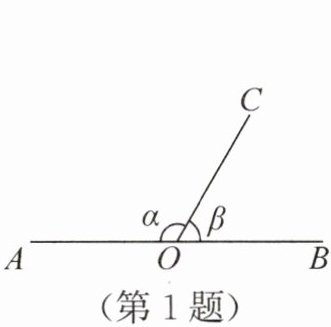
1. (3分)如图,射线 OC 的端点 O 在直线 AB 上,∠α=2∠β.下列式子的值最大的是 (
A.sinβ
B.2cosβ
C.tanβ
D.sinβcosβ
C
)
A.sinβ
B.2cosβ
C.tanβ
D.sinβcosβ
答案:1.C
解析:
解:
∵射线OC的端点O在直线AB上,
∴∠α+∠β=180°,
又∠α=2∠β,
∴2∠β+∠β=180°,解得∠β=60°.
计算各选项:
A. sinβ=sin60°=$\frac{\sqrt{3}}{2}\approx0.866$;
B. 2cosβ=2cos60°=2×$\frac{1}{2}=1$;
C. tanβ=tan60°=$\sqrt{3}\approx1.732$;
D. sinβcosβ=sin60°cos60°=$\frac{\sqrt{3}}{2}×\frac{1}{2}=\frac{\sqrt{3}}{4}\approx0.433$.
比较得:$\sqrt{3}$最大,即tanβ的值最大.
答案:C
∵射线OC的端点O在直线AB上,
∴∠α+∠β=180°,
又∠α=2∠β,
∴2∠β+∠β=180°,解得∠β=60°.
计算各选项:
A. sinβ=sin60°=$\frac{\sqrt{3}}{2}\approx0.866$;
B. 2cosβ=2cos60°=2×$\frac{1}{2}=1$;
C. tanβ=tan60°=$\sqrt{3}\approx1.732$;
D. sinβcosβ=sin60°cos60°=$\frac{\sqrt{3}}{2}×\frac{1}{2}=\frac{\sqrt{3}}{4}\approx0.433$.
比较得:$\sqrt{3}$最大,即tanβ的值最大.
答案:C
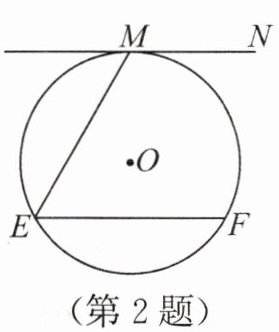
2. (3分)上分点一 如图,ME,EF 是⊙O 的弦,且 ME=EF,直线 MN 与⊙O 相切,且 EF//MN,则 cos E 的值为 (
A.$\frac{1}{3}$
B.$\frac{\sqrt{3}}{3}$
C.$\frac{1}{2}$
D.$\frac{\sqrt{3}}{2}$
C
)
A.$\frac{1}{3}$
B.$\frac{\sqrt{3}}{3}$
C.$\frac{1}{2}$
D.$\frac{\sqrt{3}}{2}$
答案:2.C
解析:
证明:连接 $OM$,$OE$,$OF$。
∵ $MN$ 与 $\odot O$ 相切于点 $M$,
∴ $OM ⊥ MN$。
∵ $EF // MN$,
∴ $OM ⊥ EF$,设垂足为 $H$,则 $EH = HF$。
∵ $ME = EF$,设 $EH = x$,则 $EF = 2x$,$ME = 2x$。
在 $Rt\triangle MHE$ 中,$MH = \sqrt{ME^2 - EH^2} = \sqrt{(2x)^2 - x^2} = \sqrt{3}x$。
设 $OH = d$,$OE = OM = r$,则 $MH = OM + OH = r + d = \sqrt{3}x$。
在 $Rt\triangle OHE$ 中,$OE^2 = OH^2 + EH^2$,即 $r^2 = d^2 + x^2$。
联立得 $\begin{cases} r + d = \sqrt{3}x \\ r^2 - d^2 = x^2 \end{cases}$,
由平方差公式 $r^2 - d^2 = (r - d)(r + d) = x^2$,代入 $r + d = \sqrt{3}x$,得 $r - d = \frac{x}{\sqrt{3}}$。
解得 $r = \frac{2x}{\sqrt{3}}$,$d = \frac{x}{\sqrt{3}}$。
在 $\triangle OME$ 中,由余弦定理:
$\cos \angle OEM = \frac{OE^2 + ME^2 - OM^2}{2 · OE · ME} = \frac{r^2 + (2x)^2 - r^2}{2 · r · 2x} = \frac{4x^2}{4xr} = \frac{x}{r} = \frac{x}{\frac{2x}{\sqrt{3}}} = \frac{\sqrt{3}}{2}$。
∵ $\angle OEM = \angle E$,
∴ $\cos E = \frac{1}{2}$。
答案:C
∵ $MN$ 与 $\odot O$ 相切于点 $M$,
∴ $OM ⊥ MN$。
∵ $EF // MN$,
∴ $OM ⊥ EF$,设垂足为 $H$,则 $EH = HF$。
∵ $ME = EF$,设 $EH = x$,则 $EF = 2x$,$ME = 2x$。
在 $Rt\triangle MHE$ 中,$MH = \sqrt{ME^2 - EH^2} = \sqrt{(2x)^2 - x^2} = \sqrt{3}x$。
设 $OH = d$,$OE = OM = r$,则 $MH = OM + OH = r + d = \sqrt{3}x$。
在 $Rt\triangle OHE$ 中,$OE^2 = OH^2 + EH^2$,即 $r^2 = d^2 + x^2$。
联立得 $\begin{cases} r + d = \sqrt{3}x \\ r^2 - d^2 = x^2 \end{cases}$,
由平方差公式 $r^2 - d^2 = (r - d)(r + d) = x^2$,代入 $r + d = \sqrt{3}x$,得 $r - d = \frac{x}{\sqrt{3}}$。
解得 $r = \frac{2x}{\sqrt{3}}$,$d = \frac{x}{\sqrt{3}}$。
在 $\triangle OME$ 中,由余弦定理:
$\cos \angle OEM = \frac{OE^2 + ME^2 - OM^2}{2 · OE · ME} = \frac{r^2 + (2x)^2 - r^2}{2 · r · 2x} = \frac{4x^2}{4xr} = \frac{x}{r} = \frac{x}{\frac{2x}{\sqrt{3}}} = \frac{\sqrt{3}}{2}$。
∵ $\angle OEM = \angle E$,
∴ $\cos E = \frac{1}{2}$。
答案:C
3. (3分)在平面直角坐标系中,点 A 与点 B($\sin60°$,$\sqrt{3}$)关于 y 轴对称.若反比例函数$y=\frac{k}{x}$的图像经过点 A,则 k=
$-\frac{3}{2}$
.答案:3.$-\frac{3}{2}$
解析:
点$ B $的坐标为$(\sin60^{\circ}, \sqrt{3})$,$\sin60^{\circ}=\frac{\sqrt{3}}{2}$,所以点$ B $的坐标为$(\frac{\sqrt{3}}{2}, \sqrt{3})$。
因为点$ A $与点$ B $关于$ y $轴对称,关于$ y $轴对称的点纵坐标相同,横坐标互为相反数,所以点$ A $的坐标为$(-\frac{\sqrt{3}}{2}, \sqrt{3})$。
反比例函数$ y = \frac{k}{x} $的图像经过点$ A $,将点$ A(-\frac{\sqrt{3}}{2}, \sqrt{3})$代入$ y = \frac{k}{x} $,可得$\sqrt{3} = \frac{k}{-\frac{\sqrt{3}}{2}}$,解得$ k = \sqrt{3} × (-\frac{\sqrt{3}}{2}) = -\frac{3}{2}$。
$-\frac{3}{2}$
因为点$ A $与点$ B $关于$ y $轴对称,关于$ y $轴对称的点纵坐标相同,横坐标互为相反数,所以点$ A $的坐标为$(-\frac{\sqrt{3}}{2}, \sqrt{3})$。
反比例函数$ y = \frac{k}{x} $的图像经过点$ A $,将点$ A(-\frac{\sqrt{3}}{2}, \sqrt{3})$代入$ y = \frac{k}{x} $,可得$\sqrt{3} = \frac{k}{-\frac{\sqrt{3}}{2}}$,解得$ k = \sqrt{3} × (-\frac{\sqrt{3}}{2}) = -\frac{3}{2}$。
$-\frac{3}{2}$
4. (3分)若锐角 x 满足$\tan^2x-(\sqrt{3}+1)\tan x+\sqrt{3}=0$,则 x=
$45°$或$60°$
.答案:4.$45°$或$60°$
解析:
解:令$t = \tan x$,则方程化为$t^2 - (\sqrt{3} + 1)t + \sqrt{3} = 0$。
因式分解得$(t - 1)(t - \sqrt{3}) = 0$,解得$t = 1$或$t = \sqrt{3}$。
当$\tan x = 1$时,$x = 45°$;当$\tan x = \sqrt{3}$时,$x = 60°$。
$45°$或$60°$
因式分解得$(t - 1)(t - \sqrt{3}) = 0$,解得$t = 1$或$t = \sqrt{3}$。
当$\tan x = 1$时,$x = 45°$;当$\tan x = \sqrt{3}$时,$x = 60°$。
$45°$或$60°$
5. (2025·江苏淮安模拟·3分)如图,在 Rt△ABC 中,∠ACB=90°,∠A<∠B,沿△ABC 的中线 CO 将△COA 折叠,使点 A 落在点 D 处.若 CD 恰好与 AB 垂直,垂足为 M,则 tan A 的值为

$\frac{\sqrt{3}}{3}$
.
答案:5.$\frac{\sqrt{3}}{3}$
解析:
证明:在Rt△ABC中,∠ACB=90°,CO是中线,
∴CO=AO=BO=$\frac{1}{2}$AB,
∴∠A=∠ACO,
由折叠性质得:∠ACO=∠DCO,OD=AO,∠D=∠A,
∴∠A=∠ACO=∠DCO,
设∠A=α,则∠ACO=∠DCO=α,
∵CD⊥AB,
∴∠DMB=90°,
∴∠D+∠DOM=90°,
∵∠DOM=∠AOC=180°-∠A-∠ACO=180°-2α,
∴α+180°-2α=90°,
解得α=30°,
∴∠A=30°,
∴tan A=tan 30°=$\frac{\sqrt{3}}{3}$.
$\frac{\sqrt{3}}{3}$
∴CO=AO=BO=$\frac{1}{2}$AB,
∴∠A=∠ACO,
由折叠性质得:∠ACO=∠DCO,OD=AO,∠D=∠A,
∴∠A=∠ACO=∠DCO,
设∠A=α,则∠ACO=∠DCO=α,
∵CD⊥AB,
∴∠DMB=90°,
∴∠D+∠DOM=90°,
∵∠DOM=∠AOC=180°-∠A-∠ACO=180°-2α,
∴α+180°-2α=90°,
解得α=30°,
∴∠A=30°,
∴tan A=tan 30°=$\frac{\sqrt{3}}{3}$.
$\frac{\sqrt{3}}{3}$
6. (6分)新素养 运算能力 计算:
(1)(2025·青海)$\sqrt{12}+(1-\sqrt{2})^0+|-\sqrt{3}|-2\sin30°$;
(2)$6\tan^230°-\sqrt{3}\sin60°-2\sin45°$;
(3)$3\tan30°-2\cos45°+2\sin60°$.
(1)(2025·青海)$\sqrt{12}+(1-\sqrt{2})^0+|-\sqrt{3}|-2\sin30°$;
(2)$6\tan^230°-\sqrt{3}\sin60°-2\sin45°$;
(3)$3\tan30°-2\cos45°+2\sin60°$.
答案:6.(1)原式$=2\sqrt{3}+1+\sqrt{3}-2 × \frac{1}{2}=3\sqrt{3}$.
(2)原式$=6 × (\frac{\sqrt{3}}{3})^2-\sqrt{3} × \frac{\sqrt{3}}{2}-2 × \frac{\sqrt{2}}{2}=2-\frac{3}{2}-\sqrt{2}=\frac{1}{2}-\sqrt{2}$.
(3)原式$=3 × \frac{\sqrt{3}}{3}-2 × \frac{\sqrt{2}}{2}+2 × \frac{\sqrt{3}}{2}=\sqrt{3}-\sqrt{2}+\sqrt{3}=2\sqrt{3}-\sqrt{2}$.
(2)原式$=6 × (\frac{\sqrt{3}}{3})^2-\sqrt{3} × \frac{\sqrt{3}}{2}-2 × \frac{\sqrt{2}}{2}=2-\frac{3}{2}-\sqrt{2}=\frac{1}{2}-\sqrt{2}$.
(3)原式$=3 × \frac{\sqrt{3}}{3}-2 × \frac{\sqrt{2}}{2}+2 × \frac{\sqrt{3}}{2}=\sqrt{3}-\sqrt{2}+\sqrt{3}=2\sqrt{3}-\sqrt{2}$.