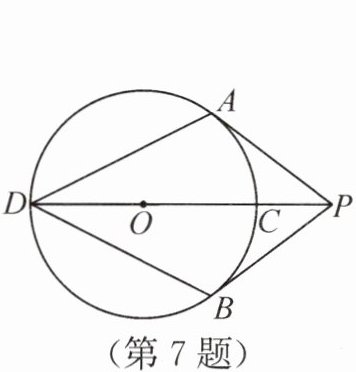
7. (3分)上分点三 如图,PA,PB分别与⊙O相切于点A,B,连接PO并延长与⊙O交于点C,D. 若CD=12,PA=8,则sin∠ADB的值为(
A.$\frac{4}{5}$
B.$\frac{3}{5}$
C.$\frac{3}{4}$
D.$\frac{4}{3}$
A
)
A.$\frac{4}{5}$
B.$\frac{3}{5}$
C.$\frac{3}{4}$
D.$\frac{4}{3}$
答案:7.A
解析:
证明:连接OA,AB。
∵PA,PB是⊙O切线,
∴OA⊥PA,OP平分∠APB,OP垂直平分AB。
∵CD=12,
∴OA=OD=6。
在Rt△OAP中,PA=8,OA=6,
∴OP=$\sqrt{OA^2+PA^2}=\sqrt{6^2+8^2}=10$。
∵∠ADB=∠PAB(同弧所对圆周角与弦切角相等),
在Rt△OAP中,sin∠PAB=sin∠ADB=$\frac{OA}{OP}=\frac{6}{10}=\frac{3}{5}$。
答案:B
∵PA,PB是⊙O切线,
∴OA⊥PA,OP平分∠APB,OP垂直平分AB。
∵CD=12,
∴OA=OD=6。
在Rt△OAP中,PA=8,OA=6,
∴OP=$\sqrt{OA^2+PA^2}=\sqrt{6^2+8^2}=10$。
∵∠ADB=∠PAB(同弧所对圆周角与弦切角相等),
在Rt△OAP中,sin∠PAB=sin∠ADB=$\frac{OA}{OP}=\frac{6}{10}=\frac{3}{5}$。
答案:B
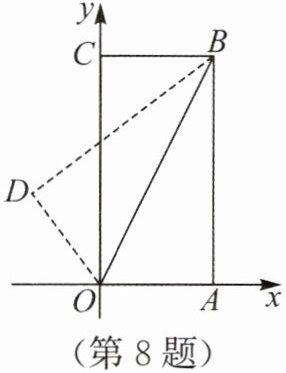
8. (3分)上分点二 如图,在平面直角坐标系中,O是原点,矩形OABC的边OA,OC分别在x轴、y轴的正半轴上,顶点B的坐标为(1,2),连接OB,将△OAB沿直线OB翻折. 若点A落在点D的位置,则cos∠COD的值为(
A.$\frac{3}{5}$
B.$\frac{1}{2}$
C.$\frac{3}{4}$
D.$\frac{4}{5}$
D
)
A.$\frac{3}{5}$
B.$\frac{1}{2}$
C.$\frac{3}{4}$
D.$\frac{4}{5}$
答案:8.D
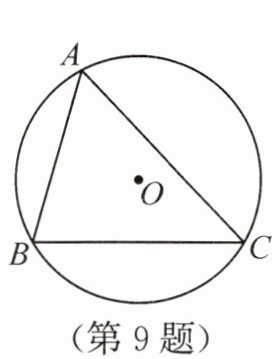
9. (2025·江苏扬州模拟·3分)如图,△ABC内接于半径为1的⊙O,∠BAC=θ(θ是锐角),则△ABC面积的最大值为(
A.$\cos\theta(1+\cos\theta)$
B.$\cos\theta(1+\sin\theta)$
C.$\sin\theta(1+\sin\theta)$
D.$\sin\theta(1+\cos\theta)$
D
)
A.$\cos\theta(1+\cos\theta)$
B.$\cos\theta(1+\sin\theta)$
C.$\sin\theta(1+\sin\theta)$
D.$\sin\theta(1+\cos\theta)$
答案:9.D 解析:过点$A$作$AD⊥ BC$于点$D$,则$\angle ADB = 90°$.因为$S_{\triangle ABC} = \frac{1}{2}BC· AD$,且$BC$的长为定值,所以当$AD$的长最大时,$S_{\triangle ABC}$取最大值.易知当点$O$在$AD$上时,$AD$的长最大,此时$BD = CD = \frac{1}{2}BC$.连接$OB$,$OC$,则$\angle BOC = 2\angle BAC$.因为$OB = OC$,所以$\angle BOD = \angle COD = \frac{1}{2}\angle BOC$,所以$\angle BOD = \angle BAC = \theta$.因为$\odot O$的半径为$1$,所以$OA = OB = 1$,所以$OD = OB·\cos\angle BOD = \cos\theta$,$BD = OB·\sin\angle BOD = \sin\theta$,所以$AD = OA + OD = 1 + \cos\theta$,$BC = 2BD = 2\sin\theta$,所以$S_{\triangle ABC} = \frac{1}{2}BC· AD = \sin\theta(1 + \cos\theta)$.故$\triangle ABC$面积的最大值为$\sin\theta(1 + \cos\theta)$.
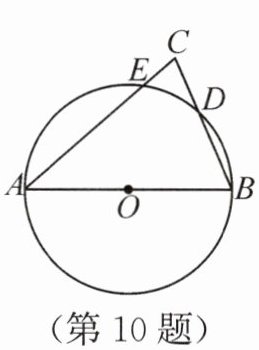
10. (3分)如图,以锐角三角形ABC的边AB为直径作⊙O,分别交AC,BC于E,D两点. 若AC=14,$\sin C=3\tan B$,则BD=
6
.
答案:10.6
解析:
证明:连接AD。
∵AB为⊙O直径,
∴∠ADB=∠AEB=90°,即AD⊥BC,AE⊥BE。
在Rt△ADC中,$\sin C=\frac{AD}{AC}=\frac{AD}{14}$。
在Rt△ABD中,$\tan B=\frac{AD}{BD}$。
∵$\sin C=3\tan B$,
∴$\frac{AD}{14}=3×\frac{AD}{BD}$。
∵AD≠0,
∴$\frac{1}{14}=\frac{3}{BD}$,解得$BD=42$。
1
∵AB为⊙O直径,
∴∠ADB=∠AEB=90°,即AD⊥BC,AE⊥BE。
在Rt△ADC中,$\sin C=\frac{AD}{AC}=\frac{AD}{14}$。
在Rt△ABD中,$\tan B=\frac{AD}{BD}$。
∵$\sin C=3\tan B$,
∴$\frac{AD}{14}=3×\frac{AD}{BD}$。
∵AD≠0,
∴$\frac{1}{14}=\frac{3}{BD}$,解得$BD=42$。
1
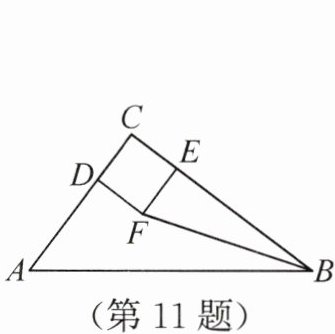
11. (3分)如图,在△ABC中,AC=3,BC=4,点D,E分别在边AC,BC上,点F在△ABC内. 若四边形CDFE是边长为1的正方形,则sin∠FBA=
$\frac{\sqrt{10}}{10}$
.
答案:11.$\frac{\sqrt{10}}{10}$
解析:
解:过点F作FG⊥AB于点G,
∵四边形CDFE是边长为1的正方形,
∴CD=CE=EF=DF=1,∠C=∠CDF=∠CEF=90°,
∵AC=3,BC=4,
∴AD=AC-CD=3-1=2,BE=BC-CE=4-1=3,
在Rt△ADF中,AD=2,DF=1,
根据勾股定理得:AF=$\sqrt{AD^2+DF^2}=\sqrt{2^2+1^2}=\sqrt{5}$,
在Rt△ABC中,AC=3,BC=4,
根据勾股定理得:AB=$\sqrt{AC^2+BC^2}=\sqrt{3^2+4^2}=5$,
设FG=h,AG=x,则BG=AB-AG=5-x,
∵S_{△ABC}=S_{△ADF}+S_{△BEF}+S_{正方形CDFE}+S_{△AFB},
S_{△ABC}=$\frac{1}{2}×AC×BC=\frac{1}{2}×3×4=6$,
S_{△ADF}=$\frac{1}{2}×AD×DF=\frac{1}{2}×2×1=1$,
S_{△BEF}=$\frac{1}{2}×BE×EF=\frac{1}{2}×3×1=\frac{3}{2}$,
S_{正方形CDFE}=1×1=1,
S_{△AFB}=$\frac{1}{2}×AB×FG=\frac{1}{2}×5×h=\frac{5}{2}h$,
∴6=1+$\frac{3}{2}$+1+$\frac{5}{2}h$,
解得h=$\frac{1}{\sqrt{10}}$,
在Rt△BFG中,BG=5-x,FG=$\frac{1}{\sqrt{10}}$,BF=$\sqrt{BG^2+FG^2}$,
又
∵在Rt△AFG中,AG=x,FG=$\frac{1}{\sqrt{10}}$,AF=$\sqrt{5}$,
∴x^2+($\frac{1}{\sqrt{10}}$)^2=($\sqrt{5}$)^2,
解得x=$\frac{7}{\sqrt{10}}$,
∴BG=5-$\frac{7}{\sqrt{10}}$,
在Rt△BFG中,sin∠FBA=$\frac{FG}{BF}=\frac{\frac{1}{\sqrt{10}}}{\sqrt{(\frac{3}{\sqrt{10}})^2+(\frac{1}{\sqrt{10}})^2}}=\frac{\sqrt{10}}{10}$。
$\frac{\sqrt{10}}{10}$
∵四边形CDFE是边长为1的正方形,
∴CD=CE=EF=DF=1,∠C=∠CDF=∠CEF=90°,
∵AC=3,BC=4,
∴AD=AC-CD=3-1=2,BE=BC-CE=4-1=3,
在Rt△ADF中,AD=2,DF=1,
根据勾股定理得:AF=$\sqrt{AD^2+DF^2}=\sqrt{2^2+1^2}=\sqrt{5}$,
在Rt△ABC中,AC=3,BC=4,
根据勾股定理得:AB=$\sqrt{AC^2+BC^2}=\sqrt{3^2+4^2}=5$,
设FG=h,AG=x,则BG=AB-AG=5-x,
∵S_{△ABC}=S_{△ADF}+S_{△BEF}+S_{正方形CDFE}+S_{△AFB},
S_{△ABC}=$\frac{1}{2}×AC×BC=\frac{1}{2}×3×4=6$,
S_{△ADF}=$\frac{1}{2}×AD×DF=\frac{1}{2}×2×1=1$,
S_{△BEF}=$\frac{1}{2}×BE×EF=\frac{1}{2}×3×1=\frac{3}{2}$,
S_{正方形CDFE}=1×1=1,
S_{△AFB}=$\frac{1}{2}×AB×FG=\frac{1}{2}×5×h=\frac{5}{2}h$,
∴6=1+$\frac{3}{2}$+1+$\frac{5}{2}h$,
解得h=$\frac{1}{\sqrt{10}}$,
在Rt△BFG中,BG=5-x,FG=$\frac{1}{\sqrt{10}}$,BF=$\sqrt{BG^2+FG^2}$,
又
∵在Rt△AFG中,AG=x,FG=$\frac{1}{\sqrt{10}}$,AF=$\sqrt{5}$,
∴x^2+($\frac{1}{\sqrt{10}}$)^2=($\sqrt{5}$)^2,
解得x=$\frac{7}{\sqrt{10}}$,
∴BG=5-$\frac{7}{\sqrt{10}}$,
在Rt△BFG中,sin∠FBA=$\frac{FG}{BF}=\frac{\frac{1}{\sqrt{10}}}{\sqrt{(\frac{3}{\sqrt{10}})^2+(\frac{1}{\sqrt{10}})^2}}=\frac{\sqrt{10}}{10}$。
$\frac{\sqrt{10}}{10}$
12. (7分)新素养 推理能力 如图,D是△ABC的边BC上一点,连接AD,作△ABD的外接圆,将△ADC沿直线AD折叠,点C的对应点E落在$\overset{\frown}{BD}$上,连接BE.
(1)求证:AB=AE;
(2)若∠CAB=90°,$\cos\angle ADB=\frac{1}{3}$,BE=2,求BC的长.

(1)求证:AB=AE;
(2)若∠CAB=90°,$\cos\angle ADB=\frac{1}{3}$,BE=2,求BC的长.

答案:12.(1)由折叠的性质,得$\angle AED = \angle ACD$,$AE = AC$.因为$\angle ABD = \angle AED$,所以$\angle ABD = \angle ACD$,所以$AB = AC$,所以$AB = AE$.
(2)过点$A$作$AH⊥ BE$于点$H$.因为$AB = AE$,$BE = 2$,所以$\angle ABE = \angle AEB$,$BH = EH = \frac{1}{2}BE = 1$.因为$\angle AEB = \angle ADB$,所以$\angle ABE = \angle ADB$,所以$\cos\angle ABE = \cos\angle ADB = \frac{1}{3}$,所以$\frac{BH}{AB} = \frac{1}{3}$,所以$AC = AB = 3$.因为$\angle CAB = 90°$,所以$BC = \sqrt{AB^2 + AC^2} = 3\sqrt{2}$.
(2)过点$A$作$AH⊥ BE$于点$H$.因为$AB = AE$,$BE = 2$,所以$\angle ABE = \angle AEB$,$BH = EH = \frac{1}{2}BE = 1$.因为$\angle AEB = \angle ADB$,所以$\angle ABE = \angle ADB$,所以$\cos\angle ABE = \cos\angle ADB = \frac{1}{3}$,所以$\frac{BH}{AB} = \frac{1}{3}$,所以$AC = AB = 3$.因为$\angle CAB = 90°$,所以$BC = \sqrt{AB^2 + AC^2} = 3\sqrt{2}$.