1. 有关圆柱的数据如下表,完成表格。
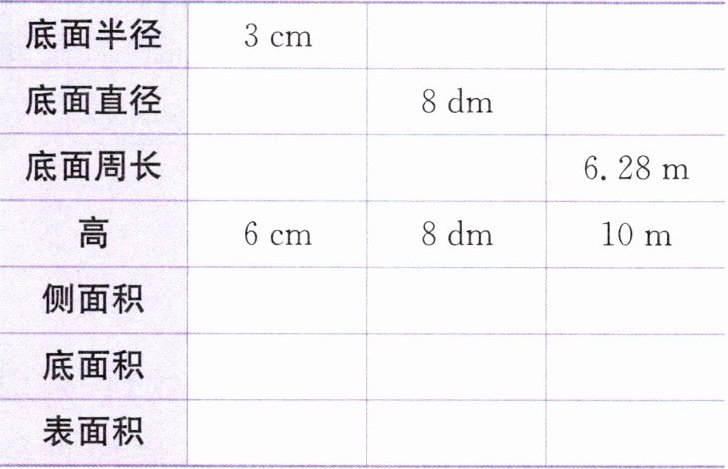

答案:1. 6 cm 18.84 cm 113.04 ${cm^2}$ 28.26 ${cm^2}$
169.56 ${cm^2}$ 4 dm 25.12 dm 200.96 ${dm^2}$
50.24 ${dm^2}$ 301.44 ${dm^2}$ 1 m 2 m 62.8 ${m^2}$
3.14 ${m^2}$ 69.08 ${m^2}$
169.56 ${cm^2}$ 4 dm 25.12 dm 200.96 ${dm^2}$
50.24 ${dm^2}$ 301.44 ${dm^2}$ 1 m 2 m 62.8 ${m^2}$
3.14 ${m^2}$ 69.08 ${m^2}$
(1)下面是四名同学测量圆锥高的方法,你认为(
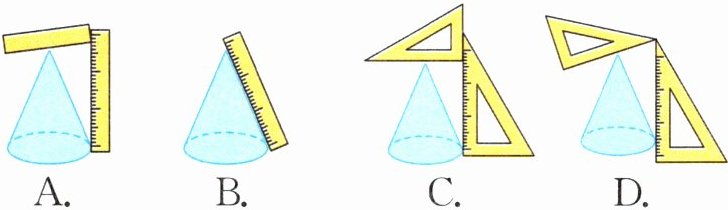
C
)的方法正确。
答案:2. (1) C
(2)把一个大圆柱切成了 2 个同样大小的小圆柱,2 个小圆柱的表面积之和比大圆柱的表面积多 5.6 dm²,大圆柱的底面积是(
A.5.6
B.1.4
C.2.8
D.3.2
C
)dm²。A.5.6
B.1.4
C.2.8
D.3.2
答案:2. (2) C
解析:
把一个大圆柱切成2个同样大小的小圆柱,增加了2个底面的面积。已知表面积之和比大圆柱多$5.6\,\mathrm{dm}^2$,则大圆柱的底面积为$5.6÷2 = 2.8\,\mathrm{dm}^2$。
C
C
3. (易错题)王叔叔要做一对没有盖的圆柱形铁皮水桶,底面半径是 2 分米,高是 10 分米。做这对水桶至少需要多少平方分米的铁皮?
答案:3. $(2×3.14×2×10+3.14×2^2)×2=276.32(平方$
分米) 易错分析:易错在审题时忽略“一对”。
分米) 易错分析:易错在审题时忽略“一对”。
4. (学科融合)连筒引水是利用斜面的原理把水从一处引到另一处。淘淘和月月用几个半圆柱形塑料槽搭一个较长的斜面,模拟连筒引水。每个塑料槽的形状如图所示,每个塑料槽用了多少平方厘米的塑料板?
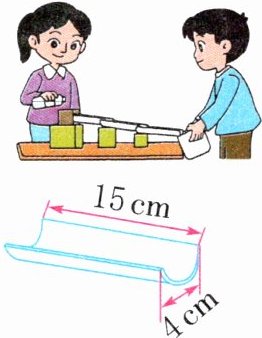

答案:4. $3.14×4×15=188.4(cm^2)$
$188.4÷2=94.2(cm^2)$
$188.4÷2=94.2(cm^2)$
5. (生活应用)制作一个带盖圆柱形水桶,有若干张如图所示的铁皮可供选择。
(1)选择型号为(
(2)制作这个圆柱形水桶需要铁皮多少平方分米?
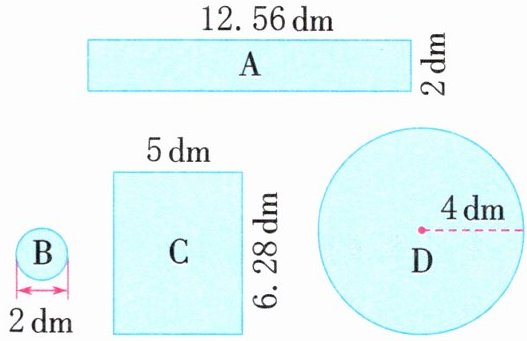
(1)选择型号为(
B
)和(C
)的铁皮比较合适。(填字母)(2)制作这个圆柱形水桶需要铁皮多少平方分米?

答案:5. (1) B C
(2) $6.28×5=31.4(dm^2)$
$3.14×(2÷2)^2×2=6.28(dm^2)$
$31.4+6.28=37.68(dm^2)$
(2) $6.28×5=31.4(dm^2)$
$3.14×(2÷2)^2×2=6.28(dm^2)$
$31.4+6.28=37.68(dm^2)$
6. (1)一个圆柱的高是 4 dm,若底面直径增加 2 cm,则它的侧面积增加(
251.2
)cm²。答案:6. (1) 251.2 解析:圆柱的侧面积=底面周长×
高,4 dm=40 cm,设圆柱的底面直径为 d cm,则原
来圆柱的侧面积为$40×3.14×d=125.6d(cm^2)$,
现在圆柱的侧面积为$40×3.14×(2+d)=(251.2+125.6d)cm^2$,所以侧面积增加$251.2+125.6d-125.6d=251.2(cm^2)$。
高,4 dm=40 cm,设圆柱的底面直径为 d cm,则原
来圆柱的侧面积为$40×3.14×d=125.6d(cm^2)$,
现在圆柱的侧面积为$40×3.14×(2+d)=(251.2+125.6d)cm^2$,所以侧面积增加$251.2+125.6d-125.6d=251.2(cm^2)$。
(2)一个圆柱的底面直径是 12 cm,如果它的高增加 2 cm,那么它的侧面积增加(
75.36
)cm²。答案:(2) 75.36 解析:圆柱的底面直径不变,高增加
2cm,则侧面积就增加以底面周长为长、2cm为宽的
长方形的面积,列式为$3.14×12×2=75.36(cm^2)$。
2cm,则侧面积就增加以底面周长为长、2cm为宽的
长方形的面积,列式为$3.14×12×2=75.36(cm^2)$。
7. 有一根圆柱形木料,如果截成 3 段小圆柱,那么表面积增加 50.24 平方分米;如果沿着底面直径且垂直于底面劈成两半,那么表面积增加 80 平方分米。这根圆柱形木料的表面积是(
150.72
)平方分米。答案:7. 150.72 解析:如果截成3段小圆柱,那么表面
积增加的部分是圆柱的4个底面的面积和,即每个
底面的面积是$50.24÷[(3-1)×2]=12.56(平方分米)$;如果沿着底面直径且垂直于底面劈成两半,
那么表面积增加的部分是2个分别以底面直径和圆
柱的高为长和宽(或宽和长)的长方形的面积,用底
面直径与圆柱的高的积乘π就得到圆柱的侧面积。
所以这根圆柱形木料的表面积为$12.56×2+3.14×(80÷2)=150.72(平方分米)$。
积增加的部分是圆柱的4个底面的面积和,即每个
底面的面积是$50.24÷[(3-1)×2]=12.56(平方分米)$;如果沿着底面直径且垂直于底面劈成两半,
那么表面积增加的部分是2个分别以底面直径和圆
柱的高为长和宽(或宽和长)的长方形的面积,用底
面直径与圆柱的高的积乘π就得到圆柱的侧面积。
所以这根圆柱形木料的表面积为$12.56×2+3.14×(80÷2)=150.72(平方分米)$。