18. 已知五个正数的和等于 5,用反证法证明这五个数中至少有一个大于或等于 1,其中,第一步应假设
这五个正数都小于1
.答案:这五个正数都小于1
19. 先判断下列命题的真假,若是真命题,请写出它的逆命题;若是假命题,请举反例说明.
(1)如果三个自然数的积是偶数,那么这三个自然数中至少有一个是偶数;
(2)在同一平面内,$ a $,$ b $,$ c $ 是直线,且 $ a // b $,$ b ⊥ c $,则 $ a // c $;
(3)相等的角是内错角.
(1)如果三个自然数的积是偶数,那么这三个自然数中至少有一个是偶数;
(2)在同一平面内,$ a $,$ b $,$ c $ 是直线,且 $ a // b $,$ b ⊥ c $,则 $ a // c $;
(3)相等的角是内错角.
答案:
19.(1)真命题 逆命题:如果三个自然数中至少有一个是偶数,那么这三个自然数的积是偶数
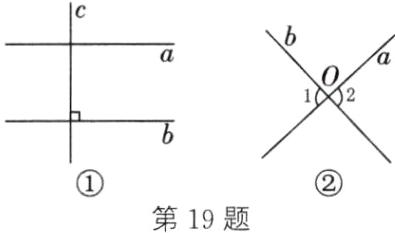
(2)假命题 如图①,满足a//b,b⊥c,但a与c不平行,
∴该命题为假命题
(3)假命题 反例不唯一,如图②,直线a与b相交于点O,∠1=∠2(对顶角相等),但∠1与∠2不是内错角,
∴该命题为假命题
19.(1)真命题 逆命题:如果三个自然数中至少有一个是偶数,那么这三个自然数的积是偶数
(2)假命题 如图①,满足a//b,b⊥c,但a与c不平行,
∴该命题为假命题
(3)假命题 反例不唯一,如图②,直线a与b相交于点O,∠1=∠2(对顶角相等),但∠1与∠2不是内错角,
∴该命题为假命题

20. 对假命题“任何一个角的补角都不小于这个角”举反例,正确的反例是(
A.$ \angle \alpha = 60^{\circ} $,$ \angle \alpha $ 的补角 $ \angle \beta = 120^{\circ} $,$ \angle \beta > \angle \alpha $
B.$ \angle \alpha = 90^{\circ} $,$ \angle \alpha $ 的补角 $ \angle \beta = 90^{\circ} $,$ \angle \beta = \angle \alpha $
C.$ \angle \alpha = 100^{\circ} $,$ \angle \alpha $ 的补角 $ \angle \beta = 80^{\circ} $,$ \angle \beta < \angle \alpha $
D.互补的两个角有一条公共边
C
)A.$ \angle \alpha = 60^{\circ} $,$ \angle \alpha $ 的补角 $ \angle \beta = 120^{\circ} $,$ \angle \beta > \angle \alpha $
B.$ \angle \alpha = 90^{\circ} $,$ \angle \alpha $ 的补角 $ \angle \beta = 90^{\circ} $,$ \angle \beta = \angle \alpha $
C.$ \angle \alpha = 100^{\circ} $,$ \angle \alpha $ 的补角 $ \angle \beta = 80^{\circ} $,$ \angle \beta < \angle \alpha $
D.互补的两个角有一条公共边
答案:C
21. 甲、乙、丙 3 人参加三项知识竞赛,每项知识竞赛第一名到第三名的得分依次为 10 分、5 分、3 分. 竞赛全部结束后,甲获得其中两项的第一名及总分第一名,则下列说法错误的是(
A.第二名、第三名的总分之和为 29 分或 31 分
B.第二名的总分可能超过 18 分
C.第三名的总分共有 3 种情况
D.第三名不可能获得其中任何一场比赛的第一名
C
)A.第二名、第三名的总分之和为 29 分或 31 分
B.第二名的总分可能超过 18 分
C.第三名的总分共有 3 种情况
D.第三名不可能获得其中任何一场比赛的第一名
答案:C 解析:依题意,甲的得分(单位:分)情况有两种:10,10,5或10,10,3,显然3人的总得分为(10 + 5 + 3)×3 = 54(分),当甲的得分(单位:分)为10,10,5时,第二名、第三名的总分之和为54 - (10 + 10 + 5)=29(分),当甲的得分(单位:分)为10,10,3时,第二名、第三名的总分之和为54 - (10 + 10 + 3)=31(分).故选项A正确,不符合题意.当甲的得分(单位:分)为10,10,5时,第二名得分(单位:分)有三种情况:5,5,10;5,3,10;3,3,10,总分分别为20分、18分、16分,第三名得分(单位:分)对应有三种情况:3,3,3;3,5,3;5,5,3,总分分别为9分、11分、13分.当甲的得分(单位:分)为10,10,3时,第二名得分(单位:分)有三种情况:5,5,10;5,3,10;3,3,10,总分分别为20分、18分、16分,第三名得分(单位:分)对应有三种情况:3,3,5;3,5,5;5,5,5,总分分别为11分、13分、15分.故选项B、D正确,不符合题意.第三名总分共有4种情况,故选项C错误,符合题意.
22. 如图,$ D $ 为 $ \triangle ABC $ 的边 $ BC $ 的延长线上一点. 若 $ \angle A:\angle ABC = 3:4 $,$ \angle ACD = 140^{\circ} $,$ \angle ABC $ 的平分线与 $ \angle ACD $ 的平分线交于点 $ M $,则 $ \angle M = $_________$^{\circ} $.
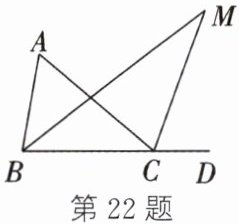

答案:30
解析:
证明:设$\angle A = 3x$,$\angle ABC = 4x$。
$\because \angle ACD$是$\triangle ABC$的外角,
$\therefore \angle ACD = \angle A + \angle ABC$,
即$140° = 3x + 4x$,
解得$x = 20°$,
$\therefore \angle ABC = 4x = 80°$。
$\because BM$平分$\angle ABC$,$CM$平分$\angle ACD$,
$\therefore \angle MBC = \frac{1}{2}\angle ABC = 40°$,
$\angle MCD = \frac{1}{2}\angle ACD = 70°$。
$\because \angle MCD$是$\triangle MBC$的外角,
$\therefore \angle MCD = \angle M + \angle MBC$,
$\therefore \angle M = \angle MCD - \angle MBC = 70° - 40° = 30°$。
$30$
$\because \angle ACD$是$\triangle ABC$的外角,
$\therefore \angle ACD = \angle A + \angle ABC$,
即$140° = 3x + 4x$,
解得$x = 20°$,
$\therefore \angle ABC = 4x = 80°$。
$\because BM$平分$\angle ABC$,$CM$平分$\angle ACD$,
$\therefore \angle MBC = \frac{1}{2}\angle ABC = 40°$,
$\angle MCD = \frac{1}{2}\angle ACD = 70°$。
$\because \angle MCD$是$\triangle MBC$的外角,
$\therefore \angle MCD = \angle M + \angle MBC$,
$\therefore \angle M = \angle MCD - \angle MBC = 70° - 40° = 30°$。
$30$
23. 如图所示为可调躺椅示意图,$ AE $ 与 $ BD $ 的交点为 $ C $,且 $ \angle A $,$ \angle B $,$ \angle E $ 保持不变. 为了舒适,需调整 $ \angle D $ 的大小,使 $ \angle EFD = 110^{\circ} $,则图中 $ \angle D $ 应

减少
(填“增加”或“减少”)10°
.
答案:减少 10°
解析:
解:在△ABC中,∠ACB=180°-∠A-∠B=180°-50°-60°=70°,
∴∠ECD=∠ACB=70°。
在△CDE中,∠D+∠E+∠ECD=180°,∠E=30°,
∴∠D=180°-∠E-∠ECD=180°-30°-70°=80°。
在△DEF中,∠EFD=110°,∠E=30°,
∴∠D'=180°-∠E-∠EFD=180°-30°-110°=40°。
原∠D=80°,调整后∠D'=40°,80°-40°=40°,
则∠D应减少40°。
1
∴∠ECD=∠ACB=70°。
在△CDE中,∠D+∠E+∠ECD=180°,∠E=30°,
∴∠D=180°-∠E-∠ECD=180°-30°-70°=80°。
在△DEF中,∠EFD=110°,∠E=30°,
∴∠D'=180°-∠E-∠EFD=180°-30°-110°=40°。
原∠D=80°,调整后∠D'=40°,80°-40°=40°,
则∠D应减少40°。
1
24. 在平面内有 $ n $ 个点,其中每三个点都能构成等腰三角形,我们把具有这样性质的 $ n $ 个点构成的点集称为“爱尔特希点集”. 如图,四边形 $ ABCD $ 的四个顶点构成“爱尔特希点集”. 若平面内存在一个点 $ P $ 与 $ A $,$ B $,$ C $,$ D $ 四个点也构成“爱尔特希点集”,则 $ \angle APB $ 的度数为
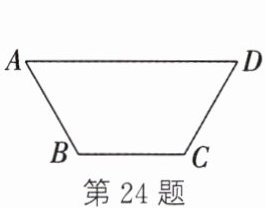
72°或36°
.
答案:72°或36° 解析:由题意,知当A,B,C,D四个点为某正五边形的四个顶点时,构成“爱尔特希点集”.当点P为正五边形的中心时,与A,B,C,D四个点构成“爱尔特希点集”,此时∠APB=72°;当点P在正五边形的顶点处(除A,B,C,D四个顶点外的另一个顶点)时,∠APB=36°.综上所述,∠APB的度数为72°或36°.
解析:
当$A$,$B$,$C$,$D$为正五边形的四个顶点时,构成“爱尔特希点集”。
若点$P$为正五边形的中心,此时$\angle APB = \frac{360°}{5} = 72°$;
若点$P$为正五边形除$A$,$B$,$C$,$D$外的另一个顶点,此时$\angle APB = 36°$。
$72°$或$36°$
若点$P$为正五边形的中心,此时$\angle APB = \frac{360°}{5} = 72°$;
若点$P$为正五边形除$A$,$B$,$C$,$D$外的另一个顶点,此时$\angle APB = 36°$。
$72°$或$36°$