6. (2024·天津)如图,在 $\triangle ABC$ 中,$\angle C = 90^{\circ}$,$\angle B = 40^{\circ}$,根据尺规作图的痕迹作射线 $AP$,与 $BC$ 相交于点 $D$,则 $\angle ADC$ 的度数为(

A.$60^{\circ}$
B.$65^{\circ}$
C.$70^{\circ}$
D.$75^{\circ}$
B
)
A.$60^{\circ}$
B.$65^{\circ}$
C.$70^{\circ}$
D.$75^{\circ}$
答案:6. B
解析:
证明:在$\triangle ABC$中,$\angle C=90^{\circ}$,$\angle B=40^{\circ}$,
$\therefore \angle BAC=180^{\circ}-\angle C-\angle B=180^{\circ}-90^{\circ}-40^{\circ}=50^{\circ}$。
由尺规作图痕迹可知,$AP$平分$\angle BAC$,
$\therefore \angle BAD=\frac{1}{2}\angle BAC=\frac{1}{2}×50^{\circ}=25^{\circ}$。
在$\triangle ABD$中,$\angle ADC=\angle B+\angle BAD=40^{\circ}+25^{\circ}=65^{\circ}$。
故答案为:B。
$\therefore \angle BAC=180^{\circ}-\angle C-\angle B=180^{\circ}-90^{\circ}-40^{\circ}=50^{\circ}$。
由尺规作图痕迹可知,$AP$平分$\angle BAC$,
$\therefore \angle BAD=\frac{1}{2}\angle BAC=\frac{1}{2}×50^{\circ}=25^{\circ}$。
在$\triangle ABD$中,$\angle ADC=\angle B+\angle BAD=40^{\circ}+25^{\circ}=65^{\circ}$。
故答案为:B。
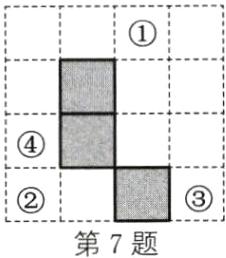
7. 如图,在 $4 × 4$ 的正方形网格中,已有三个小正方形被涂灰,再将网格中其余小正方形任意涂灰一个,使整个涂灰部分组成的图案构成一个轴对称图形的方法有

4
种.
答案:
7. 4 解析:如图,涂灰①~④中任意一个均满足题意.
7. 4 解析:如图,涂灰①~④中任意一个均满足题意.

8. (新考法·操作实践题)如图所示为由8个边长相等的正六边形组成的图形,若在5个白色的正六边形中,选择2个涂灰,使被涂灰的2个正六边形和原来3个被涂灰的正六边形恰好组成轴对称图形,则选择的方案最多有
]
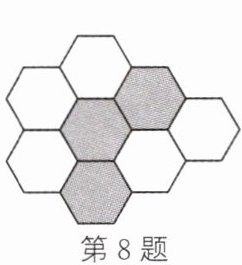
8
种.]

答案:
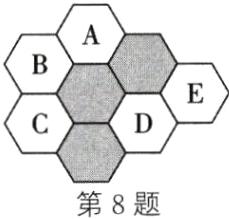
8. 8 解析:如图,涂灰的方案有:选择 AB,AC,AD,AE,BC,BD,CD,DE,共8种.
8. 8 解析:如图,涂灰的方案有:选择 AB,AC,AD,AE,BC,BD,CD,DE,共8种.

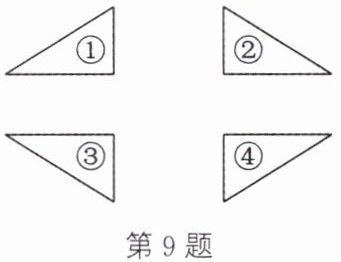
9. 如图,三角形④与哪些三角形成轴对称?整个图形是轴对称图形吗?如果是,那么它共有几条对称轴?请把它们画出来.

答案:
9. 三角形④分别与三角形②、三角形③成轴对称 整个图形是轴对称图形,它共有2条对称轴 如图,直线 l₁,l₂ 就是整个图形的对称轴
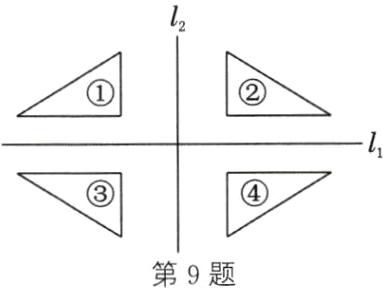
9. 三角形④分别与三角形②、三角形③成轴对称 整个图形是轴对称图形,它共有2条对称轴 如图,直线 l₁,l₂ 就是整个图形的对称轴

10. 如图,现有两张大小、形状完全一样的直角三角形纸片,将它们的一组对应边重合在一起能组成轴对称图形,请画出所有组成的轴对称图形及其对称轴(三角形不重叠).
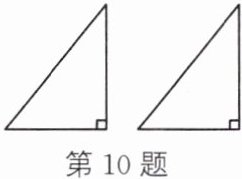

答案:
10. 如图所示
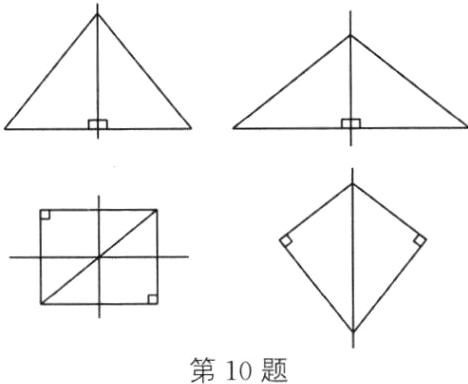
10. 如图所示
