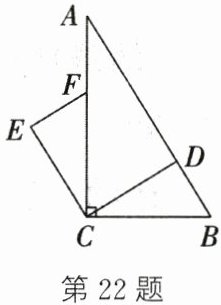
22. (10分)如图,在直角三角形 $ABC$ 中,$\angle ACB = 90^{\circ}$,点 $D$ 在边 $AB$ 上,把 $\triangle CBD$ 绕点 $C$ 逆时针旋转 $90^{\circ}$ 得到 $\triangle CFE$.
(1)$CD$ 与 $CE$ 之间的数量关系是
(2)若 $EF// CD$,试说明:$CE// AB$.
(1)$CD$ 与 $CE$ 之间的数量关系是
相等
,位置关系是垂直
;(2)若 $EF// CD$,试说明:$CE// AB$.

答案:22.(1)相等 垂直 (2)因为△CBD绕点C逆时针旋转90°得到△CFE,所以∠CDB=∠CEF,∠DCE=∠ACB=90°.因为EF//CD,所以∠CEF+∠DCE=180°,所以∠CEF=90°,所以∠CDB=90°,所以∠CDB=∠DCE,所以CE//AB
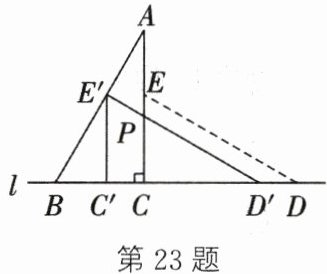
23. (10分)如图,直线 $l$ 上有两个大小相同的直角三角形(直角三角形 $ABC$ 和直角三角形 $DEC$),它们中较大锐角的度数为 $60^{\circ}$,且 $\angle ACB = 90^{\circ}$,点 $E$ 在 $AC$ 上. 将 $\triangle ECD$ 沿直线 $l$ 向左平移到 $\triangle E'C'D'$ 的位置,使点 $E$ 落在 $AB$ 上的点 $E'$ 处,$P$ 为 $AC$ 与 $E'D'$ 的交点.
(1)求 $\angle CPD'$ 的度数;
(2)试判断 $AB$ 与 $E'D'$ 之间的位置关系,并说明理由.
(1)求 $\angle CPD'$ 的度数;
(2)试判断 $AB$ 与 $E'D'$ 之间的位置关系,并说明理由.

答案:23.(1)因为△E′C′D′是由△ECD沿直线l向左平移得到的,所以DE//D′E′,所以∠CPD′=∠CED=60° (2)AB⊥E′D′
理由:因为△ACB是直角三角形,∠ACB=90°,所以∠A=180° - 90° - 60°=30°.因为△E′C′D′是由△ECD沿直线l向左平移得到的,所以CE//C′E′,∠C′E′D′=∠CED=60°,所以∠BE′C′=∠A=30°,所以∠BE′D′=∠C′E′D′+∠BE′C′=60°+30°=90°,所以AB⊥E′D′.
理由:因为△ACB是直角三角形,∠ACB=90°,所以∠A=180° - 90° - 60°=30°.因为△E′C′D′是由△ECD沿直线l向左平移得到的,所以CE//C′E′,∠C′E′D′=∠CED=60°,所以∠BE′C′=∠A=30°,所以∠BE′D′=∠C′E′D′+∠BE′C′=60°+30°=90°,所以AB⊥E′D′.
24. (10分)利用图形的变换可以解决很多生活中问题.
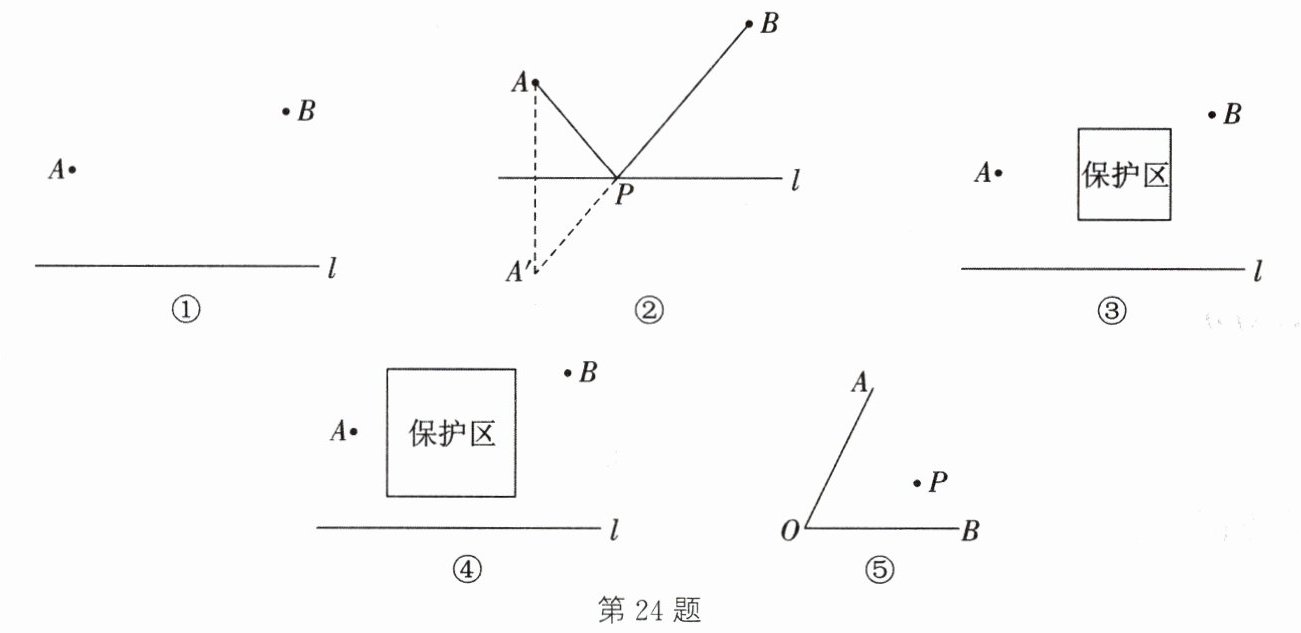
如图①,要在一条笔直的路边 $l$ 上建一个燃气站,向 $l$ 同侧的 $A$,$B$ 两个城镇分别铺设管道输送燃气. 试确定燃气站的位置,使铺设管道的路线最短.
如图②,作出点 $A$ 关于 $l$ 的对称点 $A'$,线段 $A'B$ 与直线 $l$ 的交点 $P$ 的位置即为所求,即在 $P$ 处建燃气站,所得路线 $A - P - B$ 是最短的.
(1)如果在 $A$,$B$ 两个城镇之间规划一个生态保护区,燃气管道不能穿过该区域,请分别给出如图③④所示的两种情形的铺设管道的方案(不需说明理由,作图工具不限);
(2)如图⑤,已知 $\angle AOB$ 及其内部一点 $P$,试在 $OA$,$OB$ 上分别确定点 $M$,$N$,使 $PM + PN + MN$ 最小(不需说明理由,作图工具不限).
如图①,要在一条笔直的路边 $l$ 上建一个燃气站,向 $l$ 同侧的 $A$,$B$ 两个城镇分别铺设管道输送燃气. 试确定燃气站的位置,使铺设管道的路线最短.
如图②,作出点 $A$ 关于 $l$ 的对称点 $A'$,线段 $A'B$ 与直线 $l$ 的交点 $P$ 的位置即为所求,即在 $P$ 处建燃气站,所得路线 $A - P - B$ 是最短的.
(1)如果在 $A$,$B$ 两个城镇之间规划一个生态保护区,燃气管道不能穿过该区域,请分别给出如图③④所示的两种情形的铺设管道的方案(不需说明理由,作图工具不限);
(2)如图⑤,已知 $\angle AOB$ 及其内部一点 $P$,试在 $OA$,$OB$ 上分别确定点 $M$,$N$,使 $PM + PN + MN$ 最小(不需说明理由,作图工具不限).

答案:
24.(1)如图①②所示 解析:如图①,连接BC,然后作出点C关于l的对称点C′,线段AC′与直线l的交点P的位置即为所求,即在P处建燃气站,所得路线A - P - C - B是最短的.如图②,分别连接AD,BC,然后作出点C关于l的对称点C′,线段DC′与直线l的交点P的位置即为所求,即在P处建燃气站,所得路线A - D - P - C - B是最短的.
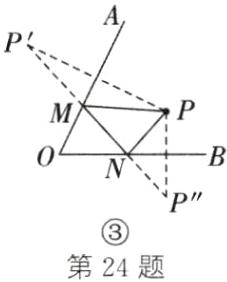
(2)如图③所示 解析:如图③,分别作出点P关于OA,OB的对称点P′,P′′,然后连接P′P′′,交OA于点M,交OB于点N,此时PM+PN+MN最小.


24.(1)如图①②所示 解析:如图①,连接BC,然后作出点C关于l的对称点C′,线段AC′与直线l的交点P的位置即为所求,即在P处建燃气站,所得路线A - P - C - B是最短的.如图②,分别连接AD,BC,然后作出点C关于l的对称点C′,线段DC′与直线l的交点P的位置即为所求,即在P处建燃气站,所得路线A - D - P - C - B是最短的.
(2)如图③所示 解析:如图③,分别作出点P关于OA,OB的对称点P′,P′′,然后连接P′P′′,交OA于点M,交OB于点N,此时PM+PN+MN最小.


