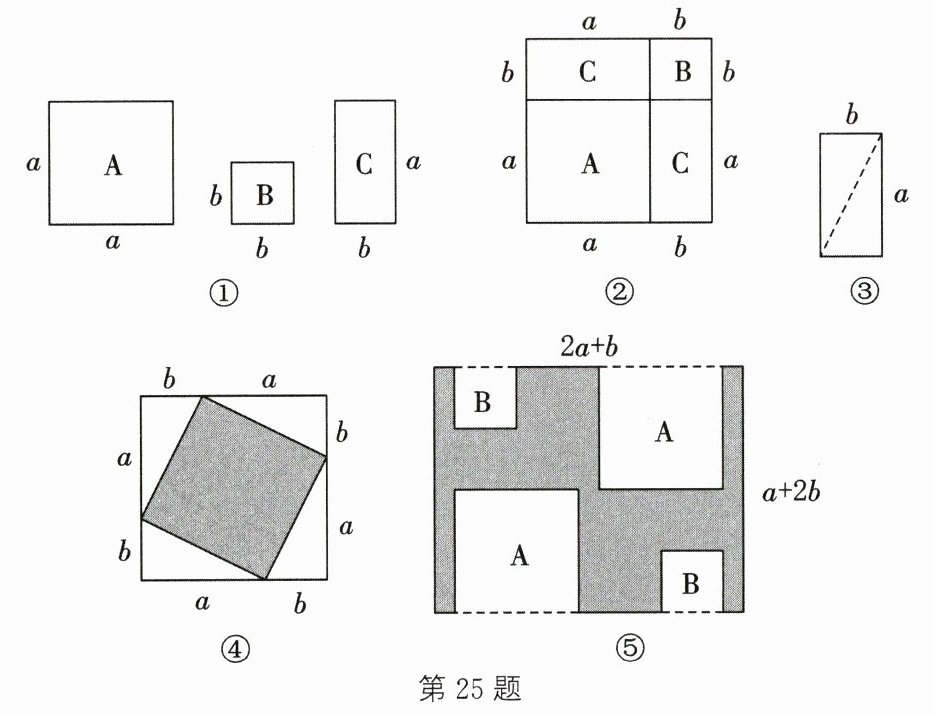
25. (10 分)如图①,现有 A,B,C 三种不同的卡片若干张,其中 A 型卡片是边长为 $ a $ 的正方形,B 型卡片是边长为 $ b(b < a) $ 的正方形,C 型卡片是长为 $ a $、宽为 $ b $ 的长方形.
(1)用上述三种卡片拼出图②,通过两种方法计算图②的面积,可以得到一个代数恒等式,请写出这个代数恒等式:
(2)将 2 张 C 型卡片沿如图③所示的虚线剪开后,拼成如图④所示的大正方形,请用含 $ a $,$ b $ 的代数式表示涂色部分的面积,即 $ S_{\mathrm{涂色部分}} = $
(3)如图⑤,在长为 $ 2a + b $、宽为 $ a + 2b $ 的长方形中挖去 A 型、B 型卡片各 2 张. 若(2)中图④涂色部分的面积为 9,而图⑤涂色部分的面积为 17.5,求图⑤涂色部分的周长.
(1)用上述三种卡片拼出图②,通过两种方法计算图②的面积,可以得到一个代数恒等式,请写出这个代数恒等式:
$(a + b)^2 = a^2 + 2ab + b^2$
.(2)将 2 张 C 型卡片沿如图③所示的虚线剪开后,拼成如图④所示的大正方形,请用含 $ a $,$ b $ 的代数式表示涂色部分的面积,即 $ S_{\mathrm{涂色部分}} = $
$(a + b)^2 - 2ab$
.(3)如图⑤,在长为 $ 2a + b $、宽为 $ a + 2b $ 的长方形中挖去 A 型、B 型卡片各 2 张. 若(2)中图④涂色部分的面积为 9,而图⑤涂色部分的面积为 17.5,求图⑤涂色部分的周长.

答案:25.(1)$(a + b)^2 = a^2 + 2ab + b^2$ (2)$(a + b)^2 - 2ab$(或$a^2 + b^2$) (3)由题图⑤,可知$(2a + b)(a + 2b) - 2a^2 - 2b^2 = 17.5$,化简,得$ab = 3.5$.由题图④,可知$(a + b)^2 - 2ab = 9$.把$ab = 3.5$代入,得$(a + b)^2 = 16$.因为$a + b > 0$,所以$a + b = 4$,所以题图⑤涂色部分的周长为$2(2a + b) + 2(a + 2b) + 2(2a + 2b) = 10(a + b) = 10×4 = 40$