22. (6 分)求证:三个连续奇数的平方和加 1 能被 12 整除。
答案:22.设三个连续奇数为2n-1,2n+1,2n+3,n是整数,
∴(2n-1)²+(2n+1)²+(2n+3)²+1=4n²-4n+1+4n²+4n+1+4n²+12n+9+1=12n²+12n+12=12(n²+n+1),
∴三个连续奇数的平方和加1能被12整除
∴(2n-1)²+(2n+1)²+(2n+3)²+1=4n²-4n+1+4n²+4n+1+4n²+12n+9+1=12n²+12n+12=12(n²+n+1),
∴三个连续奇数的平方和加1能被12整除
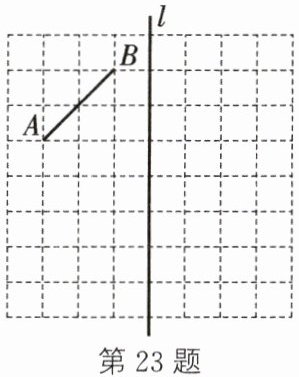
23. (8 分)如图,方格纸中每个小正方形的边长为 1 个单位长度,点 $A$,$B$ 均在格点上。
(1)画出线段 $AB$ 关于直线 $l$ 对称的线段 $CD$(点 $A$,$B$ 的对应点分别为 $C$,$D$);
(2)画出线段 $AB$ 向右平移 4 个单位长度,再向下平移 4 个单位长度后得到的线段 $EF$(点 $A$,$B$ 的对应点分别为 $E$,$F$);
(3)在(1)(2)的条件下,线段 $EF$ 可以看成由线段 $CD$ 通过一次旋转变换得到,请画出旋转中心 $O$。
(1)画出线段 $AB$ 关于直线 $l$ 对称的线段 $CD$(点 $A$,$B$ 的对应点分别为 $C$,$D$);
(2)画出线段 $AB$ 向右平移 4 个单位长度,再向下平移 4 个单位长度后得到的线段 $EF$(点 $A$,$B$ 的对应点分别为 $E$,$F$);
(3)在(1)(2)的条件下,线段 $EF$ 可以看成由线段 $CD$ 通过一次旋转变换得到,请画出旋转中心 $O$。

答案:
23.(1)如图,线段CD即为所求 (2)如图,线段EF即为所求 (3)如图,点O′和点O″即为所求 解析:连接CE,DF,分别作线段CE,DF的垂直平分线,相交于点O′,分别延长DC,EF,相交于点O″,则线段EF可以看成由线段CD绕点O′顺时针旋转90°得到或由线段CD绕点O″逆时针旋转90°得到,则点O′和点O″均满足题意.
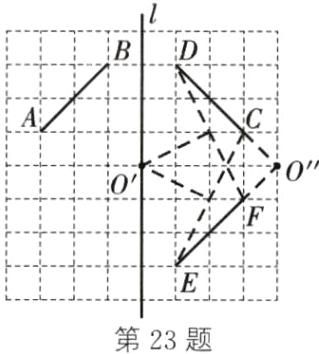
23.(1)如图,线段CD即为所求 (2)如图,线段EF即为所求 (3)如图,点O′和点O″即为所求 解析:连接CE,DF,分别作线段CE,DF的垂直平分线,相交于点O′,分别延长DC,EF,相交于点O″,则线段EF可以看成由线段CD绕点O′顺时针旋转90°得到或由线段CD绕点O″逆时针旋转90°得到,则点O′和点O″均满足题意.
