1. 新趋势 数形结合 涂一涂，填一填。
$\dfrac{1}{4}=\dfrac{(\quad)}{(\quad)}$
$\dfrac{2}{3}=\dfrac{(\quad)}{(\quad)}$
$\dfrac{3}{5}=\dfrac{(\quad)}{(\quad)}$
$\dfrac{1}{4}=\dfrac{(\quad)}{(\quad)}$
$\dfrac{2}{3}=\dfrac{(\quad)}{(\quad)}$
$\dfrac{3}{5}=\dfrac{(\quad)}{(\quad)}$
答案：
1.
$\frac{2}{8}$
$\frac{4}{6}$
$\frac{6}{10}$
1.
$\frac{2}{8}$ $\frac{4}{6}$ $\frac{6}{10}$$2. $把右面图形的$\dfrac{2}{6}$涂上红色，$\dfrac{3}{6}$涂上黄色。红色涂了$（ ）$个$\dfrac{1}{6}，$黄
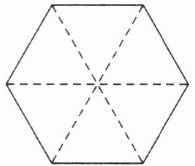
色涂了$（ ）$个$\dfrac{1}{6}，$红色和黄色一共涂了$（ ）$个$\dfrac{1}{6}，$是$\dfrac{(\quad)}{(\quad)}。$
还剩下$\dfrac{(\quad)}{(\quad)}$没涂色。
色涂了$（ ）$个$\dfrac{1}{6}，$红色和黄色一共涂了$（ ）$个$\dfrac{1}{6}，$是$\dfrac{(\quad)}{(\quad)}。$
还剩下$\dfrac{(\quad)}{(\quad)}$没涂色。
答案：
2.
2 3 5 $\frac{5}{6}$ $\frac{1}{6}$
2.
2 3 5 $\frac{5}{6}$ $\frac{1}{6}$$3. $新情境$ $生活应用$ $妈妈买回一个饼，爷爷吃了这个饼的$\dfrac{1}{8}，$奶奶吃的和爷爷一
样多，爸爸吃的是爷爷、奶奶吃的总和，爸爸吃了这个饼的$\dfrac{(\quad)}{(\quad)}。$小敏吃
了这个饼的$\dfrac{3}{8}，$小敏比爸爸多吃了这个饼的$\dfrac{(\quad)}{(\quad)}。$
样多，爸爸吃的是爷爷、奶奶吃的总和，爸爸吃了这个饼的$\dfrac{(\quad)}{(\quad)}。$小敏吃
了这个饼的$\dfrac{3}{8}，$小敏比爸爸多吃了这个饼的$\dfrac{(\quad)}{(\quad)}。$
答案：3.$\frac{2}{8}$ $\frac{1}{8}$
$4. $新趋势$ $思维过程$ \dfrac{A}{15}+\dfrac{B}{15}=\dfrac{13}{15}(A，$$B$都是大于$0$的自然数$)，$那么$A，$$B$分别
是多少$？$一共能写出$($
是多少$？$一共能写出$($
$12$
$)$组符合条件的答案。 答案：4.12 解析:根据同分母分数加法的计算方法可知,A与B的和等于13,则A,B分别可以是1,12;2,11;3,10;4,9;5,8;6,7;7,6;8,5;9,4;10,3;11,2;12,1。一共能写出12组。
解析：
因为$\dfrac{A}{15}+\dfrac{B}{15}=\dfrac{A+B}{15}=\dfrac{13}{15}$，所以$A+B=13$。
由于$A$，$B$都是大于$0$的自然数，所以可能的组合为：
$A=1$，$B=12$；
$A=2$，$B=11$；
$A=3$，$B=10$；
$A=4$，$B=9$；
$A=5$，$B=8$；
$A=6$，$B=7$；
$A=7$，$B=6$；
$A=8$，$B=5$；
$A=9$，$B=4$；
$A=10$，$B=3$；
$A=11$，$B=2$；
$A=12$，$B=1$。
一共能写出12组符合条件的答案。
由于$A$，$B$都是大于$0$的自然数，所以可能的组合为：
$A=1$，$B=12$；
$A=2$，$B=11$；
$A=3$，$B=10$；
$A=4$，$B=9$；
$A=5$，$B=8$；
$A=6$，$B=7$；
$A=7$，$B=6$；
$A=8$，$B=5$；
$A=9$，$B=4$；
$A=10$，$B=3$；
$A=11$，$B=2$；
$A=12$，$B=1$。
一共能写出12组符合条件的答案。
1. 看图列式计算。
（1）
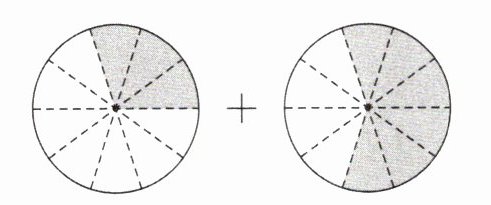
$\dfrac{(\quad)}{(\quad)}◯\dfrac{(\quad)}{(\quad)}=\dfrac{(\quad)}{(\quad)}$
（2）
$\dfrac{(\quad)}{(\quad)}◯\dfrac{(\quad)}{(\quad)}=\dfrac{(\quad)}{(\quad)}$
（1）
$\dfrac{(\quad)}{(\quad)}◯\dfrac{(\quad)}{(\quad)}=\dfrac{(\quad)}{(\quad)}$
（2）
$\dfrac{(\quad)}{(\quad)}◯\dfrac{(\quad)}{(\quad)}=\dfrac{(\quad)}{(\quad)}$
答案：1.(1)$\frac{3}{10}$+$\frac{6}{10}$=$\frac{9}{10}$ (2)$\frac{7}{8}$−$\frac{4}{8}$=$\frac{3}{8}$