1. (模型意识)观察下面的平行四边形。
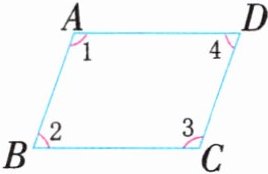
(1) 与边 $ AD $ 平行的边是(
(2) 与边 $ AB $ 长度相等的边是(
(3) 用量角器量一量,和 $ \angle 1 $ 相等的角是(
猜想:平行四边形的对角(

(1) 与边 $ AD $ 平行的边是(
BC
)。(2) 与边 $ AB $ 长度相等的边是(
DC
)。(3) 用量角器量一量,和 $ \angle 1 $ 相等的角是(
∠3
),和 $ \angle 2 $ 相等的角是(∠4
)。猜想:平行四边形的对角(
相等
)。答案:1.(1)BC (2)DC (3)∠3 ∠4 相等
解析:
(1)BC
(2)DC
(3)∠3;∠4;相等
(2)DC
(3)∠3;∠4;相等
2. (无锡真题)把一张长 16 厘米、宽 8 厘米的长方形纸对折再对折,展开后如图所示。以展开图上的 10 个点中的 4 个为顶点,画出最大的平行四边形的高是 8 厘米,与它对应的底是(
 ]
]
12
)厘米;画出高为 8 厘米的最小的等腰梯形的上底与下底的和是(16
)厘米。 ]
]答案:2.12 16
(1) 下面的说法中,正确的是(
A.梯形一定不是轴对称图形
B.梯形和平行四边形都有无数条高
C.两个完全一样的三角形不一定能拼成平行四边形
B
)。A.梯形一定不是轴对称图形
B.梯形和平行四边形都有无数条高
C.两个完全一样的三角形不一定能拼成平行四边形
答案:3.(1)B
(2) (宿迁真题)一个平行四边形相邻两条边的长度分别是 5 厘米和 7 厘米,其中一条边上的高是 6 厘米。这条高所对应的底边长度是(
A.5 厘米
B.6 厘米
C.7 厘米
A
)。A.5 厘米
B.6 厘米
C.7 厘米
答案:(2)A
解析:
假设高6厘米对应的底边为7厘米,则这条高与5厘米的边构成直角三角形,其中5厘米的边为斜边,根据直角三角形斜边大于直角边,可得5>6,不成立;假设高6厘米对应的底边为5厘米,则这条高与7厘米的边构成直角三角形,7厘米的边为斜边,7>6,成立。因此这条高所对应的底边长度是5厘米。A
4. 如图,计算梯形中 $ \angle 1 $、$ \angle 2 $、$ \angle 3 $ 的度数。


答案:4.∠1 = 180°−90°−30° = 60° ∠2 = 90°−60° = 30° ∠3 = 180°−130°−30° = 20°
5. (易错题)下图是一个梯形,找到左边的腰的中点,从该中点向下底画垂直线段得到一个三角形,把这个三角形绕中点旋转 $ 180^{\circ} $;再找到另一条腰的中点,从该中点向下底画垂直线段,也得到一个三角形,把这个三角形绕中点旋转 $ 180^{\circ} $。这时梯形就变成了一个(
 ]
]
长方形
)。画一画。 ]
]答案:
5.长方形

易错分析:这道题题干较长,容易漏看其中的操作要求导致出错,可以逐条对照进行操作,有序解题才能顺利解决问题。本题需要两次画垂直线段和两次旋转180°。
5.长方形

易错分析:这道题题干较长,容易漏看其中的操作要求导致出错,可以逐条对照进行操作,有序解题才能顺利解决问题。本题需要两次画垂直线段和两次旋转180°。
6. 一个梯形下底的长度是上底的 4 倍。如果将这个梯形的上底延长 36 厘米,那么这个梯形就成了一个平行四边形。该梯形的上底和下底分别长多少厘米?
答案:
6.上底:36÷(4−1) = 12(厘米) 下底:12×4 = 48(厘米) 解析:如图,

梯形下底的长度是上底的4倍,多的3倍正好就是36厘米,求出上底的长为12厘米,则下底的长就是48厘米。
6.上底:36÷(4−1) = 12(厘米) 下底:12×4 = 48(厘米) 解析:如图,

梯形下底的长度是上底的4倍,多的3倍正好就是36厘米,求出上底的长为12厘米,则下底的长就是48厘米。