1. 新趋势 算法探究 四年级一班的同学在雏鹰农场认领了一块长方形菜地,如图,他们在菜地里分别种了玉米、花生和黄豆。
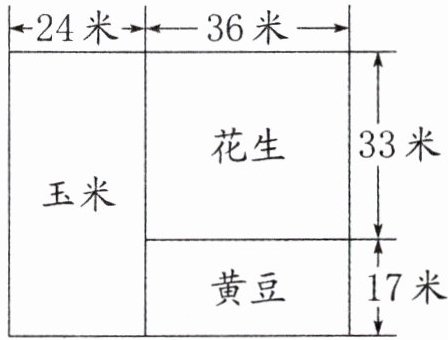
(1)欢欢列出一个算式:$33×36+17×36$,这个算式求的是(
(2)乐乐用不同的方法,同样解决了这个问题,他列的第一个算式为$33+17$,你能接着完成吗?(请列式解答)
(3)请你根据题中信息再提出一个两步或两步以上计算的问题,并解答。

(1)欢欢列出一个算式:$33×36+17×36$,这个算式求的是(
种花生和黄豆的面积
)。(2)乐乐用不同的方法,同样解决了这个问题,他列的第一个算式为$33+17$,你能接着完成吗?(请列式解答)
(3)请你根据题中信息再提出一个两步或两步以上计算的问题,并解答。
答案:1.(1)种花生和黄豆的面积
(2)33+17=50(米) 50×36=1800(平方米)
(3)答案不唯一,如种花生的面积比种黄豆的面积多多少平方米? (33−17)×36=576(平方米)
(2)33+17=50(米) 50×36=1800(平方米)
(3)答案不唯一,如种花生的面积比种黄豆的面积多多少平方米? (33−17)×36=576(平方米)
2. 新趋势 材料阅读 高斯是德国著名数学家,享有“数学王子”的美誉,他与阿基米德、牛顿、欧拉并称为世界四大数学家。高斯$10$岁时,他的老师出了下面这道题,其他学生还在思考时,他抢先说出了答案。(以下是他的计算方法)

(1)他运用了哪些运算律?请写在下面的横线上。
(2)用这种方法计算:$2+4+6+···+198+200$。

(1)他运用了哪些运算律?请写在下面的横线上。
加法交换律和加法结合律
(2)用这种方法计算:$2+4+6+···+198+200$。
答案:2.(1)加法交换律和加法结合律
(2) 2+4+6+…+198+200
=(2+200)+(4+198)+…+(100+102)
=202×50
=10100
解析:在高斯的计算方法中,他将1~100这100个数两两结合,使得每组数的和都是101,共50组数。按照同样的方法,将2+4+6+…+198+200中这100个数两两结合:2+200,4+198,6+196,…,100+102,共50组数,每组数的和都是202,则算式的结果为202×50=10100。
(2) 2+4+6+…+198+200
=(2+200)+(4+198)+…+(100+102)
=202×50
=10100
解析:在高斯的计算方法中,他将1~100这100个数两两结合,使得每组数的和都是101,共50组数。按照同样的方法,将2+4+6+…+198+200中这100个数两两结合:2+200,4+198,6+196,…,100+102,共50组数,每组数的和都是202,则算式的结果为202×50=10100。