(1) 6 和 27 的最大公因数是(
3
),最小公倍数是(54
)。答案:1.(1)3 54
(2) 用边长为(
1
)分米或(3
)分米或(9
)分米的正方形都正好能铺满长 27 分米、宽 18 分米的长方形。(填自然数)答案:1.(2)1 3 9
(3) 舞蹈组的同学排成 6 人一排或 9 人一排,都正好排完,舞蹈组最少有(
18
)人。答案:1.(3)18
(4) 妇女节那一天,王老师买来 50 多枝蓝玫瑰,每 8 枝一束或每 12 枝一束都多 4 枝,王老师一共买了(
52
)枝蓝玫瑰。答案:1.(4)52
解析:
8和12的最小公倍数是24。
24×2=48,48+4=52。
24×3=72,72+4=76(超过50多,舍去)。
52
24×2=48,48+4=52。
24×3=72,72+4=76(超过50多,舍去)。
52
(5) 甲数$=2×3×a$,乙数$=3×5×a$,$a$为大于 1 的自然数,则这两个数的最大公因数是(
3a
)。答案:1.(5)3a
2. 在(
7 和 5(
7 和 35(
12 和 24(
1
)里写出每组数的最大公因数,在[35
]里写出每组数的最小公倍数。7 和 5(
1
)[35
] 6 和 20(2
)[60
]7 和 35(
7
)[35
] 5 和 9(1
)[45
]12 和 24(
12
)[24
] 30 和 18(6
)[90
]答案:2.1 35 2 60 7 35 1 45 12 24 6 90
解析:
7 和 5(1)[35] 6 和 20(2)[60]
7 和 35(7)[35] 5 和 9(1)[45]
12 和 24(12)[24] 30 和 18(6)[90]
7 和 35(7)[35] 5 和 9(1)[45]
12 和 24(12)[24] 30 和 18(6)[90]
(1)(数形结合)甲和乙两个非 0 自然数的关系如图所示,则它们的最大公因数是(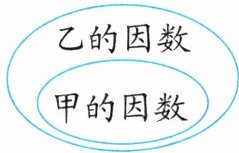
A.甲
B.乙
C.1
D.甲×乙
A
),最小公倍数是(B
)。
A.甲
B.乙
C.1
D.甲×乙
答案:3.(1)A B
(2) 如果$a$和$b$是相邻的两个非 0 自然数,那么$a$和$b$的最小公倍数是(
A.1
B.$a$
C.$b$
D.$ab$
D
),最大公因数是(A
)。A.1
B.$a$
C.$b$
D.$ab$
答案:3.(2)D A
(3) 两个合数的最大公因数是 1,最小公倍数是 144,这两个数是(
A.8、18
B.1、144
C.9、16
D.4、36
C
)。A.8、18
B.1、144
C.9、16
D.4、36
答案:3.(3)C
(4) $A$、$B$两个数的最大公因数是 34,$C$、$D$两个数的最大公因数是 51,则$A$、$B$、$C$、$D$这四个数的最大公因数是(
A.34
B.17
C.102
D.51
B
)。A.34
B.17
C.102
D.51
答案:3.(4)B
解析:
因为$A$、$B$的最大公因数是$34$,$34 = 2×17$;$C$、$D$的最大公因数是$51$,$51 = 3×17$。所以$A$、$B$、$C$、$D$这四个数的最大公因数是$34$和$51$的最大公因数,即$17$。
B
B
4. (生活应用)张叔叔和李叔叔所在公司有 56 名男员工和 48 名女员工,5 月 4 日青年节那天将举行户外登山团建活动。
(1) 把男员工和女员工都平均分成若干小组,且每组的人数相同,每组最多有几人?一共分成了几个小组?
(2) 公司按照一定的规律为员工进行排班,7 月的部分排班表如下。7 月张叔叔和李叔叔同时休息是哪几日?

(1) 把男员工和女员工都平均分成若干小组,且每组的人数相同,每组最多有几人?一共分成了几个小组?
(2) 公司按照一定的规律为员工进行排班,7 月的部分排班表如下。7 月张叔叔和李叔叔同时休息是哪几日?

答案:4.(1)(56,48)=8 每组最多有8人 56÷8+48÷8=13(个)
(2)[3,4]=12 7月12日、24日
(2)[3,4]=12 7月12日、24日
5. (数学文化)今有物,不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?(从小到大写出两个符合条件的数)


答案:5.23、128 解析:先从“三三数之剩二,七七数之剩二”入手,说明这个数是3和7的公倍数加2,符合条件的数是23,44,65,86,107,128,⋯,其中23,128是符合“五五数之剩三”的最小的两个数。
解析:
23、128