1. 用分数表示下面各图中的涂色部分。
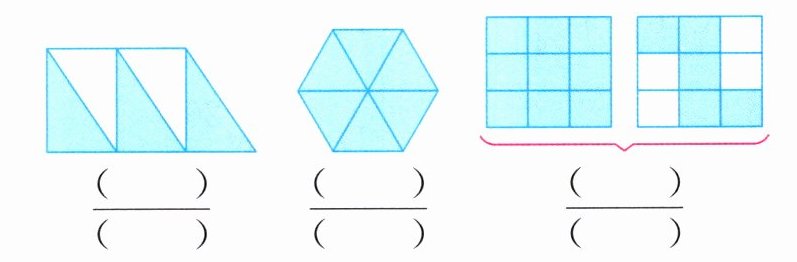

答案:1. $\frac{3}{5}$ $\frac{6}{6}$ $\frac{14}{9}$
2. 在下面各图中涂色表示其下面的分数。
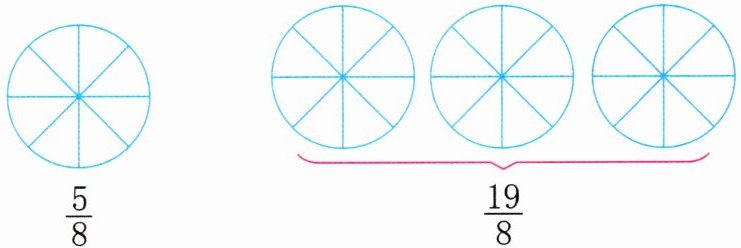

答案:
2.
2.

(1)在$□$里填合适的分数。
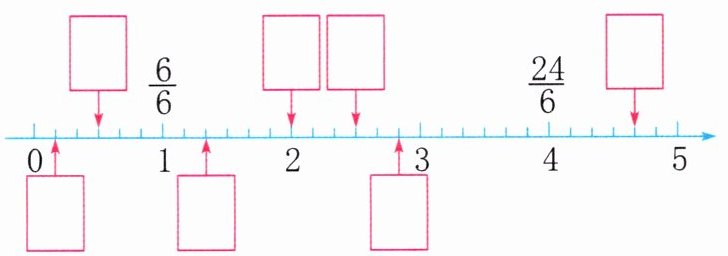

答案:
3. (1)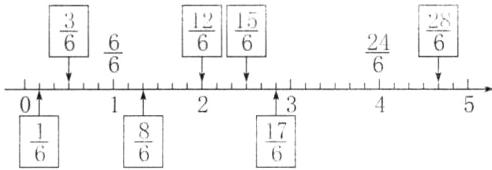
3. (1)

(2)11 个$\frac{1}{9}$是(
$\frac{11}{9}$
),$\frac{17}{10}$里面有(17
)个$\frac{1}{10}$,(12
)个$\frac{1}{12}$是 1。答案:3. (2)$\frac{11}{9}$ 17 12
(3)在$\frac{3}{5}$、$\frac{4}{4}$、$\frac{11}{6}$、$\frac{13}{14}$、$\frac{14}{13}$、$\frac{21}{19}$、$\frac{100}{100}$中,真分数有(
2
)个,假分数有(5
)个。答案:3. (3)2 5
(4)分数单位是$\frac{1}{8}$的最大真分数是(
$\frac{7}{8}$
),最小假分数是($\frac{8}{8}$
)。答案:3. (4)$\frac{7}{8}$ $\frac{8}{8}$
(5)红气球有$a$个,黄气球有$b$个,红气球的个数是黄气球的$\frac{(\quad)}{(\quad)}$,若这个分数是真分数,则说明(
红气球比黄气球少
);若这个分数是假分数,则说明(红气球不少于黄气球
)。($a$、$b$均不为 0)答案:3. (5)$\frac{a}{b}$ 红气球比黄气球少 红气球不少于黄气球
(1)(连云港真题)甲、乙、丙、丁四个数在直线上的位置如图所示,(

A.甲
B.乙
C.丙
D.丁
B
)可能是$\frac{7}{3}$。
A.甲
B.乙
C.丙
D.丁
答案:4. (1)B
解析:
$\frac{7}{3} \approx 2.33$,由图可知乙在2和3之间且靠近2,故乙可能是$\frac{7}{3}$。
B
B
(2)分子是 6 的假分数有(
A.5
B.6
C.7
D.无数
B
)个,分母是 6 的假分数有(D
)个。A.5
B.6
C.7
D.无数
答案:4. (2)B D
解析:
分子是6的假分数,分母需满足$1\leq 分母\leq 6$且为正整数,分母可为1,2,3,4,5,6,共6个;分母是6的假分数,分子需满足$分子\geq 6$且为正整数,分子有无数个。
B D
B D
(3)(推理意识)如果$\frac{10}{x}$是假分数,那么$\frac{x}{10}$的值一定(
A.大于
B.小于
C.不小于
D.不大于
D
)1。A.大于
B.小于
C.不小于
D.不大于
答案:4. (3)D
(4)下面的说法中,正确的是(
A.真分数都比 1 小,假分数都比 1 大
B.假分数的分子都比分母大
C.假分数都比真分数大
D.分母是 5 的真分数有 5 个
C
)。A.真分数都比 1 小,假分数都比 1 大
B.假分数的分子都比分母大
C.假分数都比真分数大
D.分母是 5 的真分数有 5 个
答案:4. (4)C
5. (易错题)3 千克黄豆可以制成 10 千克豆腐。照这样计算,制 1 千克豆腐需要多少千克黄豆?1 千克黄豆可制成多少千克豆腐?
答案:5. 3÷10=$\frac{3}{10}$(千克) 10÷3=$\frac{10}{3}$(千克)
易错分析:两个问题的被除数容易混淆,求制1千克豆腐需要多少千克黄豆,用黄豆的千克数作被除数;求1 千克黄豆可制成多少千克豆腐,用豆腐的千克数作被除数
易错分析:两个问题的被除数容易混淆,求制1千克豆腐需要多少千克黄豆,用黄豆的千克数作被除数;求1 千克黄豆可制成多少千克豆腐,用豆腐的千克数作被除数
6. 从 2、3、5、8 中任选两个数组成不同的分数。

答案:6. 6个,分别是$\frac{3}{2}$、$\frac{5}{2}$、$\frac{8}{2}$、$\frac{5}{3}$、$\frac{8}{3}$、$\frac{8}{5}$
7. 一个真分数,分子与分母的和是 23,如果分母减去 2,分子加上 5,那么它就成了假分数。符合条件的分数有哪些?
答案:7. $\frac{11}{12}$、$\frac{10}{13}$、$\frac{9}{14}$、$\frac{8}{15}$ 解析:先用$\frac{11}{12}$尝试,$\frac{11}{12}$的分母减去2,分子加上5是$\frac{16}{10}$,符合要求,再依次调整$\frac{11}{12}$的分子、分母,得$\frac{10}{13}$、$\frac{9}{14}$、$\frac{8}{15}$符合条件,$\frac{7}{16}$不符合条件。
解析:
设这个真分数的分子为$x$,分母为$y$。
因为分子与分母的和是$23$,所以$x + y = 23$,即$y = 23 - x$。
由于是真分数,所以$x < y$,即$x < 23 - x$,解得$x < 11.5$,所以$x$为小于等于$11$的正整数。
分母减去$2$,分子加上$5$后变成假分数,此时分子为$x + 5$,分母为$y - 2 = 23 - x - 2 = 21 - x$,所以$x + 5 \geq 21 - x$,解得$2x \geq 16$,即$x \geq 8$。
综上,$x$的取值为$8$、$9$、$10$、$11$。
当$x = 8$时,$y = 23 - 8 = 15$,分数为$\frac{8}{15}$;
当$x = 9$时,$y = 23 - 9 = 14$,分数为$\frac{9}{14}$;
当$x = 10$时,$y = 23 - 10 = 13$,分数为$\frac{10}{13}$;
当$x = 11$时,$y = 23 - 11 = 12$,分数为$\frac{11}{12}$。
符合条件的分数有:$\frac{8}{15}$、$\frac{9}{14}$、$\frac{10}{13}$、$\frac{11}{12}$。
因为分子与分母的和是$23$,所以$x + y = 23$,即$y = 23 - x$。
由于是真分数,所以$x < y$,即$x < 23 - x$,解得$x < 11.5$,所以$x$为小于等于$11$的正整数。
分母减去$2$,分子加上$5$后变成假分数,此时分子为$x + 5$,分母为$y - 2 = 23 - x - 2 = 21 - x$,所以$x + 5 \geq 21 - x$,解得$2x \geq 16$,即$x \geq 8$。
综上,$x$的取值为$8$、$9$、$10$、$11$。
当$x = 8$时,$y = 23 - 8 = 15$,分数为$\frac{8}{15}$;
当$x = 9$时,$y = 23 - 9 = 14$,分数为$\frac{9}{14}$;
当$x = 10$时,$y = 23 - 10 = 13$,分数为$\frac{10}{13}$;
当$x = 11$时,$y = 23 - 11 = 12$,分数为$\frac{11}{12}$。
符合条件的分数有:$\frac{8}{15}$、$\frac{9}{14}$、$\frac{10}{13}$、$\frac{11}{12}$。