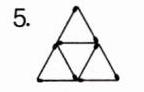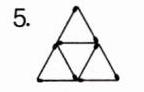1. 下面的图形中,是等边三角形的在括号里画“√”。
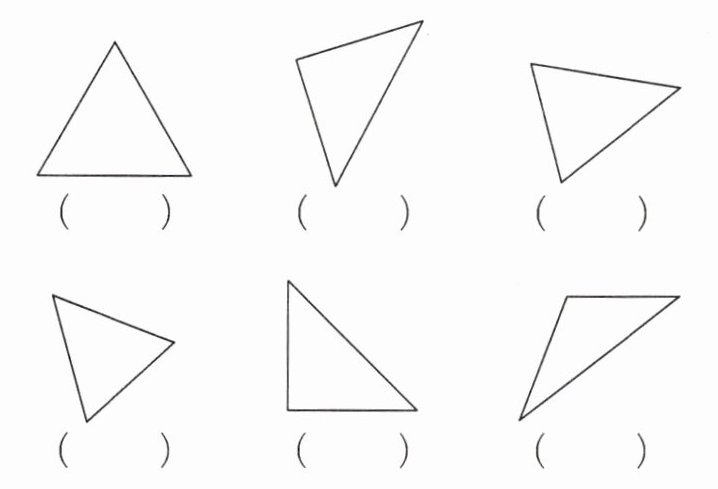

答案:1. (√) ( ) ( )
( ) ( ) ( )
【提示】依据“三条边都相等的三角形是等边三角形”进行判断。
( ) ( ) ( )
【提示】依据“三条边都相等的三角形是等边三角形”进行判断。
2. 填一填。
(1) 一个等腰三角形的顶角是 $ 36^{\circ} $,它的底角是(
(1) 一个等腰三角形的顶角是 $ 36^{\circ} $,它的底角是(
72
)$ ^{\circ} $,按角分,它是(锐角
)三角形。答案:2. (1)72 锐角 【提示】可根据等腰三角形的性质以及三角形内角和是 180°来求解底角的度数,再根
(2) 一个等腰三角形,它的顶角是其中一个底角的 $ 2 $ 倍,它的顶角是()$ ^{\circ} $。
答案:90
解析:
设底角为$x$度,则顶角为$2x$度。因为等腰三角形两底角相等,三角形内角和为$180^{\circ}$,所以$x + x + 2x = 180$,$4x = 180$,$x = 45$,顶角为$2x = 90$。
(3) 一个等腰三角形的周长是 $ 55 $ 厘米,底比一条腰短 $ 5 $ 厘米。它的底是()厘米。
答案:15
解析:
设等腰三角形的腰长为$x$厘米,则底边长为$(x - 5)$厘米。
根据等腰三角形周长公式可得$x+x+(x - 5)=55$,
即$3x-5 = 55$,
移项可得$3x=55 + 5$,
$3x=60$,
解得$x = 20$。
那么底边长为$20-5 = 15$(厘米)。
根据等腰三角形周长公式可得$x+x+(x - 5)=55$,
即$3x-5 = 55$,
移项可得$3x=55 + 5$,
$3x=60$,
解得$x = 20$。
那么底边长为$20-5 = 15$(厘米)。
3. 有一堆碎纸片(如下图)。
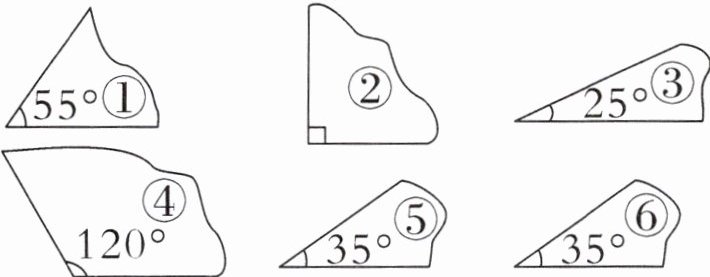
浩博认为一定能从中挑出 $ 3 $ 张纸片,使它们对应的三个角凑在一起能拼成一个等腰三角形,你同意他的想法吗?写出你的理由。

浩博认为一定能从中挑出 $ 3 $ 张纸片,使它们对应的三个角凑在一起能拼成一个等腰三角形,你同意他的想法吗?写出你的理由。
答案:不同意。
理由:等腰三角形需满足内角和180°且至少两个角相等。
现有角:55°、90°、25°、120°、35°、35°。
可能组合分析:
1. 两个35°(⑤⑥)需第三个角110°,无此角;
2. 其他角均唯一,无法形成两个相等角;
3. 和为180°的组合(如55°+90°+35°、25°+120°+35°)均无相等角。
故无法挑出3张纸片拼成等腰三角形。
理由:等腰三角形需满足内角和180°且至少两个角相等。
现有角:55°、90°、25°、120°、35°、35°。
可能组合分析:
1. 两个35°(⑤⑥)需第三个角110°,无此角;
2. 其他角均唯一,无法形成两个相等角;
3. 和为180°的组合(如55°+90°+35°、25°+120°+35°)均无相等角。
故无法挑出3张纸片拼成等腰三角形。
4. 按要求画图。
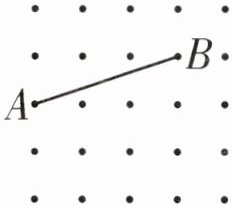
(1) 在点子图中,以 $ AB $ 为一条边,画出一个等腰三角形 $ ABC $(三角形的顶点都在点子上)。
(2) 画出三角形以 $ AB $ 为底的高。

(1) 在点子图中,以 $ AB $ 为一条边,画出一个等腰三角形 $ ABC $(三角形的顶点都在点子上)。
(2) 画出三角形以 $ AB $ 为底的高。
答案:
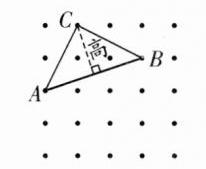

5. 实验班原创 几何直观 下图是用 $ 9 $ 根火柴棒摆成的 $ 3 $ 个等边三角形,现在只移动其中的 $ 3 $ 根火柴棒,使 $ 3 $ 个等边三角形变成 $ 5 $ 个。你能办到吗?请画出移动后的示意图。


答案: