1. 若一个直角三角形的两个锐角相差$20^{\circ}$,则较小的锐角是(
$35^{\circ}$
)。答案:1. $35^{\circ}$ 【提示】直角三角形中两个锐角的和是 $90^{\circ}$,较小的锐角的 $2$ 倍是 $90^{\circ}-20^{\circ}=70^{\circ}$,所以较小的锐角是 $70^{\circ}÷2 = 35^{\circ}$。
解析:
直角三角形中两个锐角的和是$90^{\circ}$,设较小的锐角为$x$,则另一个锐角为$x + 20^{\circ}$。可得方程$x+(x + 20^{\circ})=90^{\circ}$,即$2x+20^{\circ}=90^{\circ}$,$2x=90^{\circ}-20^{\circ}=70^{\circ}$,解得$x=35^{\circ}$。
$35^{\circ}$
$35^{\circ}$
2. 如左下图,相机的三脚架放在地面上,三个支点在地面上组成了一个三角形,这运用了(
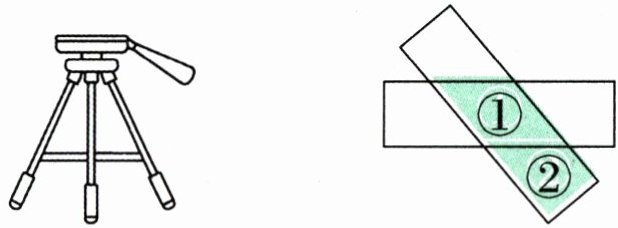
三角形的稳定性
)原理。
答案:2. 三角形的稳定性 【提示】三角形具有稳定性。
解析:
三角形的稳定性
3. 如右上图,将两张长方形纸交叉摆放,形成了两个不同的涂色部分:①和②。涂色部分①为重叠部分,是(
平行四边
)形,理由是(两组对边都平行
);涂色部分②是(梯
)形,理由是(只有一组对边平行
)。答案:3. 平行四边 两组对边都平行 梯 只有一组对边平行 【提示】平行四边形两组对边都平行,梯形只有一组对边平行。
解析:
平行四边;两组对边都平行;梯;只有一组对边平行
4. 如左下图,梯形是由一张长方形纸折叠而成的(单位:厘米)。这个梯形的下底是(
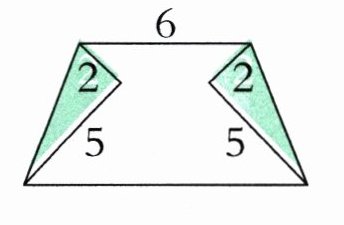
10
)厘米,高是(5
)厘米。
答案:4. $10$ $5$ 【提示】下底 $=2 + 6 + 2 = 10$(厘米)
解析:
下底:$2 + 6 + 2 = 10$(厘米)
高:$5$(厘米)
高:$5$(厘米)
5. 如右上图,点$A$沿着虚线向左不断移动,三角形$ABC$的内角和(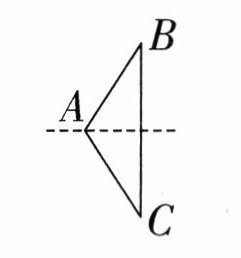
不变
)。
答案:5. 不变 【提示】任意三角形的内角和都是 $180^{\circ}$。
6. 一个等腰三角形,其中两条边分别长6厘米、9厘米,周长是(
21或24
)厘米;若它的一个底角是$65^{\circ}$,则顶角是(50
)$^{\circ}$,按角分,它是一个(锐角
)三角形。答案:6. $21$ 或 $24$ $50$ 锐角 【提示】根据三角形两边长度的和大于第三边,$6$ 和 $9$ 都可以作为腰。$180^{\circ}-65^{\circ}-65^{\circ}=50^{\circ}$。
解析:
21或24;50;锐角
7. 如下图,在一张长$10cm$、宽$6cm$的长方形纸上剪去两个等边三角形②和③后,剩下了图形①,图形①的周长是(
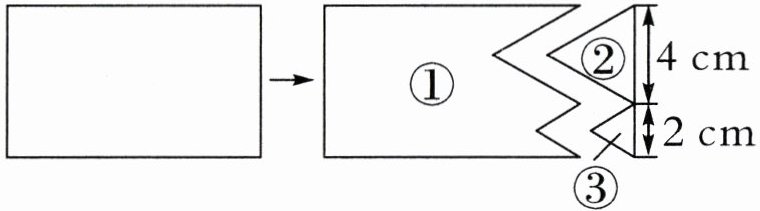
38
)$cm$。
答案:7. $38$ 【提示】观察图可知,图①的周长是原来图形的周长再加上图②、图③的一条边,$(10 + 6)×2 + 4 + 2 = 38$(厘米)。
解析:
$(10+6)×2+4+2=38$(厘米)
8. 用2根4厘米和2根6厘米的小棒中的若干根围三角形。一共能围成(
3
)种不同的三角形,其中周长最长的三角形的周长是(20
)厘米。答案:8. $3$ $20$ 【提示】第一种三边长分别为:$4$ 厘米、$4$ 厘米、$6$ 厘米;第二种三边长分别为:$6$ 厘米、$6$ 厘米、$4$ 厘米;第三种三边长分别为:$6$ 厘米、$6$ 厘米、$8$ 厘米。
9. 一个平行四边形框架的底是7厘米,高是4厘米,将它拉成一个长方形后,高比原来增加了1厘米,则原来平行四边形的周长是(
24
)厘米。答案:9. $24$ 【提示】原来平行四边形的周长是 $(7 + 4 + 1)×2 = 24$(厘米)。
解析:
将平行四边形拉成长方形后,底不变仍为7厘米,此时高为$4 + 1=5$厘米。因为长方形的宽等于平行四边形的另一条边,所以平行四边形的另一条边长为5厘米。则原来平行四边形的周长是$(7 + 5)×2 = 24$厘米。
24
24