3. 下面是星光小学一至五年级部分班级信箱示意图。
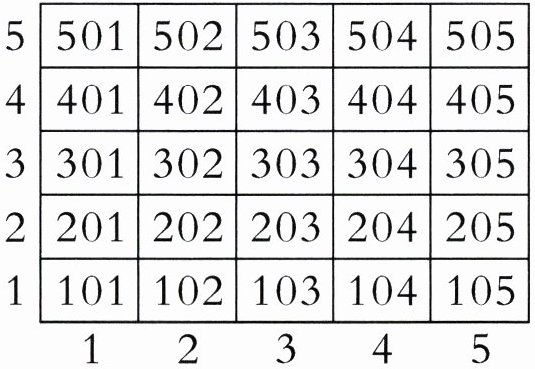
(1)203班(二年级三班)信箱的位置用数对表示是( , ),数对$(3,5)$的位置是(
(2)传达室大爷把寄给小芳的贺卡放在了$(△,2)$的信箱里,小芳是几年级的学生?

(1)203班(二年级三班)信箱的位置用数对表示是( , ),数对$(3,5)$的位置是(
五
)年级(三
)班的信箱。(2)传达室大爷把寄给小芳的贺卡放在了$(△,2)$的信箱里,小芳是几年级的学生?
答案:3. (1)(3,2) 五 三 【提示】数对中第一个数表示列,第二个数表示行。
(2)二年级 【提示】数对的后一个数表示行,第 2 行都是二年级的信箱。
(2)二年级 【提示】数对的后一个数表示行,第 2 行都是二年级的信箱。
4. 邮政编码都是由六个数字组成的。某地区的邮政编码有如下规律:这六个数字的和是15,前两个数字的和是8,第一个数字比第二个数字多2,第三个数字比6多1。该地区的邮政编码是什么?
答案:4. 537000 【提示】第 1 个数字是(8 + 2)÷2 = 5,第 2 个数字是 5 - 2 = 3,第 3 个数字是 6 + 1 = 7,已有的 3 个数字之和是 15,其余 3 个数字都是 0。
解析:
第一个数字:$(8 + 2)÷2 = 5$
第二个数字:$5 - 2 = 3$
第三个数字:$6 + 1 = 7$
前三个数字之和:$5 + 3 + 7 = 15$
后三个数字之和:$15 - 15 = 0$
后三个数字均为0
邮政编码是537000
第二个数字:$5 - 2 = 3$
第三个数字:$6 + 1 = 7$
前三个数字之和:$5 + 3 + 7 = 15$
后三个数字之和:$15 - 15 = 0$
后三个数字均为0
邮政编码是537000
一片树林里的树木排成了一个方阵,一棵柏树在这个方阵的最角落处,它的位置用数对表示是$(15,15)$,这片树林最外面三层共有多少棵树?


答案:(15 - 1)×4 = 56(棵)
15 - 2 = 13(棵)
(13 - 1)×4 = 48(棵)
13 - 2 = 11(棵)
(11 - 1)×4 = 40(棵)
56 + 48 + 40 = 144(棵)
【提示】因为柏树的位置用数对表示是(15,15),且在方阵最角落处,所以可知这片方阵树林的最外圈每边有 15 棵树。方阵最外层树的数量公式为(边长 - 1)×4,则边长为 15 时,最外层树的数量为(15 - 1)×4 = 56(棵)。第二层每边的树的数量比最外层每边少 2 棵,即边长为 15 - 2 = 13,则第二层树的数量为(13 - 1)×4 = 48(棵);第三层每边的树的数量比第二层每边又少 2 棵,即边长为 13 - 2 = 11,则第三层树的数量为(11 - 1)×4 = 40(棵)。将三层树的数量相加,可得总数为 56 + 48 + 40 = 144(棵)。
15 - 2 = 13(棵)
(13 - 1)×4 = 48(棵)
13 - 2 = 11(棵)
(11 - 1)×4 = 40(棵)
56 + 48 + 40 = 144(棵)
【提示】因为柏树的位置用数对表示是(15,15),且在方阵最角落处,所以可知这片方阵树林的最外圈每边有 15 棵树。方阵最外层树的数量公式为(边长 - 1)×4,则边长为 15 时,最外层树的数量为(15 - 1)×4 = 56(棵)。第二层每边的树的数量比最外层每边少 2 棵,即边长为 15 - 2 = 13,则第二层树的数量为(13 - 1)×4 = 48(棵);第三层每边的树的数量比第二层每边又少 2 棵,即边长为 13 - 2 = 11,则第三层树的数量为(11 - 1)×4 = 40(棵)。将三层树的数量相加,可得总数为 56 + 48 + 40 = 144(棵)。