例1
平行四边形 $ABCD$ 向右平移后得到平行四边形 $EFGH$,已知点 $A$ 用数对表示是 $(4,5)$,则点 $F$ 用数对表示是( , ),点 $C$ 用数对表示是( , )。(小方格的每条边表示 $1$)
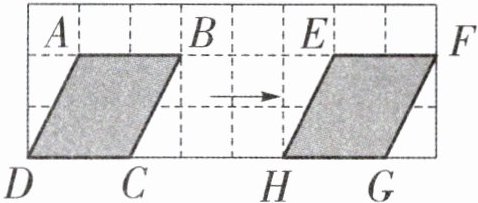
平行四边形 $ABCD$ 向右平移后得到平行四边形 $EFGH$,已知点 $A$ 用数对表示是 $(4,5)$,则点 $F$ 用数对表示是( , ),点 $C$ 用数对表示是( , )。(小方格的每条边表示 $1$)

答案:思路分析
根据点 $A$ 用数对表示是 $(4,5)$,推导出点 $B$ 用数对表示就是 $(6,5)$。从点 $B$ 到点 $F$,向右平移了 $5$ 格,点 $F$ 用数对表示就是 $(11,5)$;点 $C$ 的位置在点 $A$ 和点 $B$ 中间一列,下面两行,用数对表示就是 $(5,3)$。
解答
$(11,5)$ $(5,3)$
归纳点拨
根据数对表示的意义及各点在图中的位置,可以推导出其他各点的位置。
根据点 $A$ 用数对表示是 $(4,5)$,推导出点 $B$ 用数对表示就是 $(6,5)$。从点 $B$ 到点 $F$,向右平移了 $5$ 格,点 $F$ 用数对表示就是 $(11,5)$;点 $C$ 的位置在点 $A$ 和点 $B$ 中间一列,下面两行,用数对表示就是 $(5,3)$。
解答
$(11,5)$ $(5,3)$
归纳点拨
根据数对表示的意义及各点在图中的位置,可以推导出其他各点的位置。
1. 填一填,画一画。
(1) 用数对表示图中三角形三个顶点 $A$、$B$、$C$ 的位置。
$A$( , ) $B$( , ) $C$( , )
(2) 将图中三角形 $ABC$ 先向左平移 $4$ 格,再向下平移 $3$ 格,画出平移后的图形 $A'B'C'$,并用数对表示点 $A'$、$B'$、$C'$ 的位置。
$A'$( , ) $B'$( , ) $C'$( , )
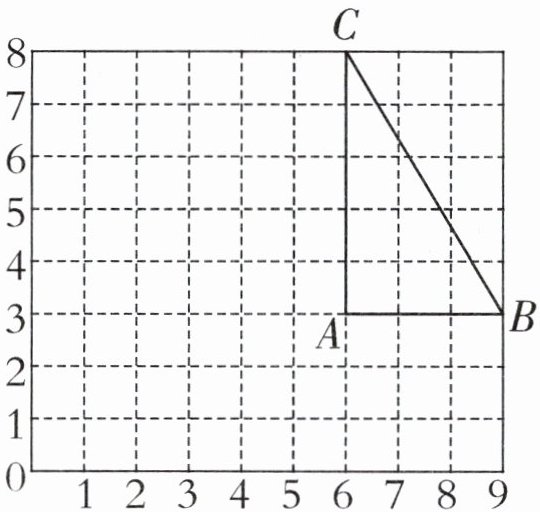
(1) 用数对表示图中三角形三个顶点 $A$、$B$、$C$ 的位置。
$A$( , ) $B$( , ) $C$( , )
(2) 将图中三角形 $ABC$ 先向左平移 $4$ 格,再向下平移 $3$ 格,画出平移后的图形 $A'B'C'$,并用数对表示点 $A'$、$B'$、$C'$ 的位置。
$A'$( , ) $B'$( , ) $C'$( , )

答案:
1. (1) (6,3) (9,3) (6,8)
(2)
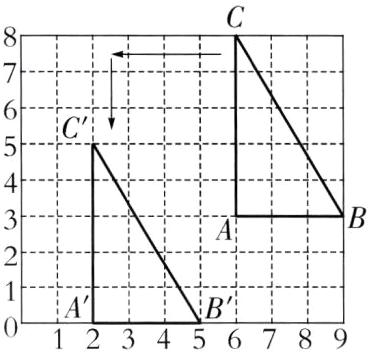
(2,0) (5,0) (2,5)
【提示】用数对表示位置时,第一个数表示列,第二个数表示行。
1. (1) (6,3) (9,3) (6,8)
(2)

(2,0) (5,0) (2,5)
【提示】用数对表示位置时,第一个数表示列,第二个数表示行。
例2
四(1)班教室里有 $8$ 列座位,每列人数相同,第 $8$ 列最后一名学生的座位用数对表示是 $(8,6)$。四(1)班一共有()名学生。
四(1)班教室里有 $8$ 列座位,每列人数相同,第 $8$ 列最后一名学生的座位用数对表示是 $(8,6)$。四(1)班一共有()名学生。
答案:思路分析
教室里的座位有 $8$ 列,每列人数相同,第 $8$ 列最后一名学生的座位用数对表示是 $(8,6)$,说明四(1)班教室里坐了 $8$ 列学生,每列有 $6$ 人,一共有 $6×8 = 48$(名)学生。
解答
$48$
归纳点拨
根据题中已知的条件确定列数和每列的人数就可以求出全班总人数。
教室里的座位有 $8$ 列,每列人数相同,第 $8$ 列最后一名学生的座位用数对表示是 $(8,6)$,说明四(1)班教室里坐了 $8$ 列学生,每列有 $6$ 人,一共有 $6×8 = 48$(名)学生。
解答
$48$
归纳点拨
根据题中已知的条件确定列数和每列的人数就可以求出全班总人数。