5. 甲、乙两车的速度比是$4:3$,两车分别从$A$、$B$两地同时开出,相向而行。相遇时甲车行驶了48千米,乙车行驶了(
A.$16$
B.$64$
C.$36$
D.$84$
C
)千米。A.$16$
B.$64$
C.$36$
D.$84$
答案:5. C 【提示】时间相同,速度比=路程比,再按比例分配求出乙车行驶的路程。
6. 将一个边长是4米的正方形按照$1:100$的比画在纸上,纸上画出的正方形的面积是(
A.$1600$平方厘米
B.$16$平方厘米
C.$16$平方米
D.$400$平方厘米
B
)。A.$1600$平方厘米
B.$16$平方厘米
C.$16$平方米
D.$400$平方厘米
答案:6. B 【提示】先求出图上正方形的边长,再根据“正方形面积=边长×边长”求出图上正方形的面积。
7. 如右下图,三角形边$a$上的高为$b$,边$c$上的高为$d$。根据这些信息,下列式子中,不成立的是(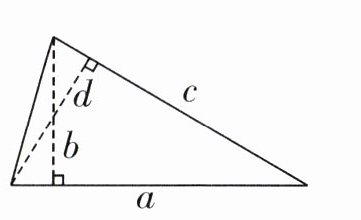
A.$a:c = d:b$
B.$a:c = b:d$
C.$\frac{a}{d} = \frac{c}{b}$
D.$\frac{a}{c} = \frac{d}{b}$
B
)。
A.$a:c = d:b$
B.$a:c = b:d$
C.$\frac{a}{d} = \frac{c}{b}$
D.$\frac{a}{c} = \frac{d}{b}$
答案:7. B 【提示】先根据三角形对应高与底的乘积除以2相等写出等式,再转化成比例。
8. “黄金比”是公认的具有重要审美意义的比,人体中藏着“黄金比”。以肚脐为分割点,当上半身与下半身的比是$5:8$时,身材显得最美,达不到的话可以用穿高跟鞋来改善。妈妈的身高是165厘米,下半身长100厘米,她穿的高跟鞋高度为(
A.$3$
B.$4$
C.$6$
D.$5$
B
)厘米时,身材显得最美。A.$3$
B.$4$
C.$6$
D.$5$
答案:8. B 【提示】先求出上半身的长度,再根据黄金比求出含高跟鞋的下半身长度,再用含高跟鞋的下半身长度减下半身长度求解。
三、解比例。(共18分)
$0.5:\frac{1}{5} = \frac{5}{2}:x$
$x:\frac{1}{4} = \frac{2}{3}:\frac{3}{5}$
$\frac{x}{4} = \frac{0.35}{0.6}$
$\frac{2.5}{x} = \frac{7.5}{2}$
$3.2:\frac{4}{5} = \frac{0.84}{x}$
$\frac{1}{2}:\frac{1}{5} = \frac{1}{4}:x$
$0.5:\frac{1}{5} = \frac{5}{2}:x$
$x:\frac{1}{4} = \frac{2}{3}:\frac{3}{5}$
$\frac{x}{4} = \frac{0.35}{0.6}$
$\frac{2.5}{x} = \frac{7.5}{2}$
$3.2:\frac{4}{5} = \frac{0.84}{x}$
$\frac{1}{2}:\frac{1}{5} = \frac{1}{4}:x$
答案:三、x=1 x=$\frac{5}{18}$ x=$\frac{7}{3}$
x=$\frac{2}{3}$ x=$\frac{21}{100}$ x=$\frac{1}{10}$
x=$\frac{2}{3}$ x=$\frac{21}{100}$ x=$\frac{1}{10}$
四、动手操作。(每题6分,共12分)
1. 填一填,画一画。(每个小方格的边长表示1cm)
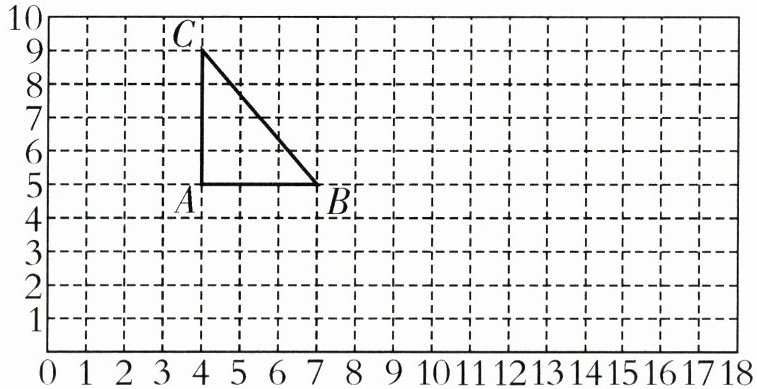
(1)图中点$A$的位置用数对$(4,5)$表示,点$B$的位置用数对( , )表示,点$C$的位置用数对( , )表示。
(2)在方格纸上画出三角形$ABC$按$2:1$的比放大后的图形。
(3)在方格纸上画一个与三角形$ABC$面积相等的平行四边形。
1. 填一填,画一画。(每个小方格的边长表示1cm)

(1)图中点$A$的位置用数对$(4,5)$表示,点$B$的位置用数对( , )表示,点$C$的位置用数对( , )表示。
(2)在方格纸上画出三角形$ABC$按$2:1$的比放大后的图形。
(3)在方格纸上画一个与三角形$ABC$面积相等的平行四边形。
答案:(1)
数对的前一个数表示列,后一个数表示行。
点$B$在第$7$列,第$5$行,所以点$B$的位置用数对$(7,5)$表示;
点$C$在第$4$列,第$9$行,所以点$C$的位置用数对$(4,9)$表示。
(2)【提示】放大后,三角形的底占6格,高占8格。
三角形$ABC$按$2:1$的比放大,就是把三角形$ABC$的各边长度放大到原来的$2$倍。
原三角形$AB$边的长度为$\vert7 - 4\vert=3cm$,放大后$A'B'$边的长度为$3×2 = 6cm$;原三角形$AC$边的长度为$\vert9 - 5\vert = 4cm$,放大后$A'C'$边的长度为$4×2=8cm$。
先确定$A'(4×2,5×2)=(8,10)$(注:这里是按比例放大后顶点的一种确定方式,也可根据数对的变化规律,$A(4,5)$,放大后$A'$列数$4$变为$4×2 = 8$,行数$5$变为$5×2 = 10$),$B'(7×2,5×2)=(14,10)$,$C'(4×2,9×2)=(8,18)$,然后连接$A'B'$,$B'C'$,$C'A'$画出放大后的图形。
(3)平行四边形的面积为3×4÷2=6(平方厘米)。
先求三角形$ABC$的面积,根据三角形面积公式$S=\frac{1}{2}×底×高$,$AB$为底$a = 3cm$,$AC$为高$h = 4cm$,则$S_{△ ABC}=\frac{1}{2}×3×4=6cm^{2}$。
对于平行四边形,根据平行四边形面积公式$S = 底×高$,可以画底为$3cm$,高为$2cm$的平行四边形(答案不唯一),例如底在第$2$列到第$5$列,高从第$3$行到第$5$行,四个顶点可以是$(2,3)$,$(5,3)$,$(5,5)$,$(2,5)$。
故答案依次为:(1)$(7,5)$;$(4,9)$。
数对的前一个数表示列,后一个数表示行。
点$B$在第$7$列,第$5$行,所以点$B$的位置用数对$(7,5)$表示;
点$C$在第$4$列,第$9$行,所以点$C$的位置用数对$(4,9)$表示。
(2)【提示】放大后,三角形的底占6格,高占8格。
三角形$ABC$按$2:1$的比放大,就是把三角形$ABC$的各边长度放大到原来的$2$倍。
原三角形$AB$边的长度为$\vert7 - 4\vert=3cm$,放大后$A'B'$边的长度为$3×2 = 6cm$;原三角形$AC$边的长度为$\vert9 - 5\vert = 4cm$,放大后$A'C'$边的长度为$4×2=8cm$。
先确定$A'(4×2,5×2)=(8,10)$(注:这里是按比例放大后顶点的一种确定方式,也可根据数对的变化规律,$A(4,5)$,放大后$A'$列数$4$变为$4×2 = 8$,行数$5$变为$5×2 = 10$),$B'(7×2,5×2)=(14,10)$,$C'(4×2,9×2)=(8,18)$,然后连接$A'B'$,$B'C'$,$C'A'$画出放大后的图形。
(3)平行四边形的面积为3×4÷2=6(平方厘米)。
先求三角形$ABC$的面积,根据三角形面积公式$S=\frac{1}{2}×底×高$,$AB$为底$a = 3cm$,$AC$为高$h = 4cm$,则$S_{△ ABC}=\frac{1}{2}×3×4=6cm^{2}$。
对于平行四边形,根据平行四边形面积公式$S = 底×高$,可以画底为$3cm$,高为$2cm$的平行四边形(答案不唯一),例如底在第$2$列到第$5$列,高从第$3$行到第$5$行,四个顶点可以是$(2,3)$,$(5,3)$,$(5,5)$,$(2,5)$。
故答案依次为:(1)$(7,5)$;$(4,9)$。