一、填一填。（每空1分，共15分）
1. 写出比值是$\frac{3}{5}$的两个比：（
1. 写出比值是$\frac{3}{5}$的两个比：（
答案不唯一，如：3:5
）和（6:10
），将它们组成比例是（3:5=6:10
）。答案：1. 答案不唯一，如：3:5 6:10
3:5=6:10 【提示】两数相比所得的值就是比值，任意
写出比值是 $\frac{3}{5}$ 的两个比即可。
3:5=6:10 【提示】两数相比所得的值就是比值，任意
写出比值是 $\frac{3}{5}$ 的两个比即可。
2. 若$5x = 4y$（$x$、$y$均不为0），则$x:y =$（
4:5
），若$y = 30$，则$x =$（24
）。答案：2. 4:5 24 【提示】由题目可知，5x=4y，则x:y=4:5，若y=30，则x=24。
解析：
4:5；24
3. 一幅地图的比例尺是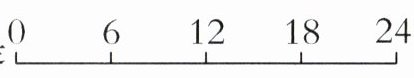
，把它改写成数值比例尺是(
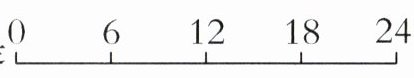，把它改写成数值比例尺是(1:600000
)；如果在图上量得甲地到乙地的距离是3厘米，那么甲地到乙地的实际距离是(18
)千米。答案：3. 1:600000 18 【提示】6千米=600000厘米，实际距离=图上距离÷比例尺。
解析：
1:600000；18
4. 一个圆形机器零件的直径是4毫米，工程师把这个零件画在了比例尺是$8:1$的图纸上，图纸上的零件的直径是(
3.2
)厘米。答案：4. 3.2 【提示】图上距离=实际距离×比例尺
解析：
4毫米=0.4厘米
图上距离=实际距离×比例尺=0.4×8=3.2厘米
3.2
图上距离=实际距离×比例尺=0.4×8=3.2厘米
3.2
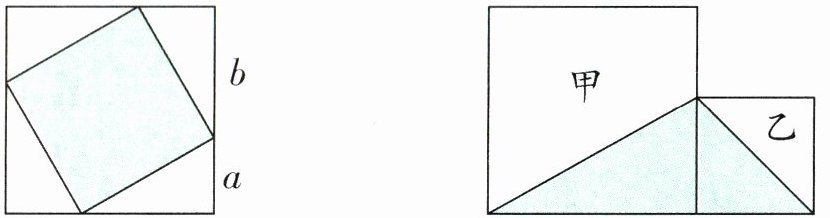
5. 如左下图，4个相同的直角三角形拼成了一个正方形，已知$a:b = 1:2$，则涂色部分的面积占大正方形面积的(
$\frac{5}{9}$
)。答案：5. $\frac{5}{9}$ 【提示】由a:b=1:2，可假设a=1，b=2，则大正方形的面积为(1+2)×(1+2)=9，4个三角形的面积和为1×2÷2×4=4，则涂色部分的面积占大正方形面积的(9-4)÷9=$\frac{5}{9}$。
解析：
因为$a:b = 1:2$，设$a = 1$，$b = 2$。
大正方形边长为$a + b=1 + 2=3$，面积为$3×3 = 9$。
一个直角三角形面积为$\frac{1×2}{2}=1$，4个三角形面积和为$1×4 = 4$。
涂色部分面积为$9 - 4=5$，占大正方形面积的$\frac{5}{9}$。
$\frac{5}{9}$
大正方形边长为$a + b=1 + 2=3$，面积为$3×3 = 9$。
一个直角三角形面积为$\frac{1×2}{2}=1$，4个三角形面积和为$1×4 = 4$。
涂色部分面积为$9 - 4=5$，占大正方形面积的$\frac{5}{9}$。
$\frac{5}{9}$
6. 如右上图，两个正方形中涂色部分的面积比是$2:1$，如果空白部分甲的面积是2.4平方分米，那么两个正方形的面积之和是(
4
)平方分米。答案：6. 4 【提示】已知涂色部分两个小三角形的面积比是2:1，高都是小正方形的边长，高相同，则涂色部分两个小三角形的底之比是2:1，也就是两个正方形的边长之比是2:1，则大正方形与小正方形的面积之比是4:1。将小正方形的面积看作1份，则大正方形的面积是这样的4份，由题可知甲的面积是这样的3份，即可求出1份的面积为2.4÷(4-1)=0.8(平方分米)，也就是小正方形的面积，进而可以求出两个正方形的面积之和，即0.8×4+0.8=4(平方分米)。
解析：
设小正方形边长为$a$，大正方形边长为$b$。
涂色部分为两个等高（高为$a$）的三角形，面积比$2:1$，则底之比为$2:1$，即$b:a = 2:1$，故$b = 2a$。
大正方形面积$b^2=(2a)^2 = 4a^2$，小正方形面积$a^2$，面积比$4:1$。
空白部分甲面积为大正方形面积减去大三角形面积：$b^2-\frac{1}{2}b· a=4a^2-\frac{1}{2}·2a· a = 3a^2$。
已知甲面积$3a^2 = 2.4$，则$a^2=0.8$。
两个正方形面积之和为$4a^2 + a^2=5a^2=5×0.8 = 4$平方分米。
4
涂色部分为两个等高（高为$a$）的三角形，面积比$2:1$，则底之比为$2:1$，即$b:a = 2:1$，故$b = 2a$。
大正方形面积$b^2=(2a)^2 = 4a^2$，小正方形面积$a^2$，面积比$4:1$。
空白部分甲面积为大正方形面积减去大三角形面积：$b^2-\frac{1}{2}b· a=4a^2-\frac{1}{2}·2a· a = 3a^2$。
已知甲面积$3a^2 = 2.4$，则$a^2=0.8$。
两个正方形面积之和为$4a^2 + a^2=5a^2=5×0.8 = 4$平方分米。
4
7. 在比例$5:30 = 12:72$中，若30减去5，要使比例依然成立，则72应减去（
12
）。答案：7. 12 【提示】原比例为5:30=12:72，当30减去5后变为25，需要找到72应减去的数，使得新比例5:25=12:x成立(其中x为72减去一个数后的结果)，解得x=60，即72应减去72-60=12。
解析：
30减去5后变为25，设72应减去的数为$x$，则新比例为$5:25 = 12:(72 - x)$。
因为比例内项之积等于外项之积，所以$5×(72 - x)=25×12$。
$5×(72 - x)=300$
$72 - x = 300÷5$
$72 - x = 60$
$x = 72 - 60$
$x = 12$
12
因为比例内项之积等于外项之积，所以$5×(72 - x)=25×12$。
$5×(72 - x)=300$
$72 - x = 300÷5$
$72 - x = 60$
$x = 72 - 60$
$x = 12$
12
8. 一个半径为2厘米的圆，按$3:1$的比放大后，圆的面积是（
113.04
）平方厘米；按（1:2
）的比缩小后，圆的面积是3.14平方厘米。答案：8. 113.04 1:2 【提示】按3:1的比放大后圆的半径是2×3=6(厘米)，根据圆的面积公式计算出放大后圆的面积为3.14×6²=113.04(平方厘米)。原来圆的面积是3.14×2²=12.56(平方厘米)，缩小后圆的面积变为3.14平方厘米，圆的面积缩小到原来的$\frac{1}{4}$，因为面积比是半径比的平方，所以半径缩小到原来的$\frac{1}{2}$，即按1:2的比缩小。
解析：
按$3:1$的比放大后圆的半径是$2×3 = 6$厘米，面积为$3.14×6^{2}=3.14×36 = 113.04$平方厘米；原来圆的面积是$3.14×2^{2}=12.56$平方厘米，缩小后面积为$3.14$平方厘米，面积比为$3.14:12.56 = 1:4$，则半径比为$1:2$。
113.04；1:2
113.04；1:2
9. 已知一个比例的两个内项互为倒数，若两个外项的和是$\frac{17}{4}$，则这两个外项分别是(
4
)和($\frac{1}{4}$
)。答案：9. 4 $\frac{1}{4}$ 【提示】根据比例的基本性质，两个外项的积等于两个内项的积。已知两个内项互为倒数，它们的积为1，因此两个外项的积也为1。再结合两个外项的和为$\frac{17}{4}$，推导出两个外项分别是4和$\frac{1}{4}$。
解析：
设两个外项分别为$a$和$b$。
因为比例的两个内项互为倒数，所以两个内项的积为$1$。根据比例的基本性质，两个外项的积等于两个内项的积，可得$a × b=1$。
又已知两个外项的和是$\frac{17}{4}$，即$a + b=\frac{17}{4}$。
联立方程$\begin{cases}ab = 1\\a + b=\frac{17}{4}\end{cases}$，解得$\begin{cases}a = 4\\b=\frac{1}{4}\end{cases}$或$\begin{cases}a=\frac{1}{4}\\b = 4\end{cases}$。
4；$\frac{1}{4}$
因为比例的两个内项互为倒数，所以两个内项的积为$1$。根据比例的基本性质，两个外项的积等于两个内项的积，可得$a × b=1$。
又已知两个外项的和是$\frac{17}{4}$，即$a + b=\frac{17}{4}$。
联立方程$\begin{cases}ab = 1\\a + b=\frac{17}{4}\end{cases}$，解得$\begin{cases}a = 4\\b=\frac{1}{4}\end{cases}$或$\begin{cases}a=\frac{1}{4}\\b = 4\end{cases}$。
4；$\frac{1}{4}$
1. 下面各组数中，能组成比例的是(
A.$12$，$8$，$\frac{1}{2}$和$\frac{1}{3}$
B.$77$，$3$，$21$和$24$
C.$0.75$，$2$，$1.25$和$5$
D.$1$，$2$，$3$和$4$
A
)。A.$12$，$8$，$\frac{1}{2}$和$\frac{1}{3}$
B.$77$，$3$，$21$和$24$
C.$0.75$，$2$，$1.25$和$5$
D.$1$，$2$，$3$和$4$
答案：1. A 【提示】两两之积相等的4个数能组成比例。
2. 有四幅不同的地图，用图上3厘米的距离表示的实际距离最短的比例尺是(
A.$1:50000$
B.$1:40000$
C.$1:30000$
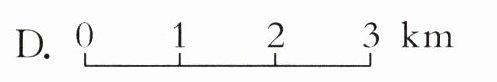
C
)。A.$1:50000$
B.$1:40000$
C.$1:30000$
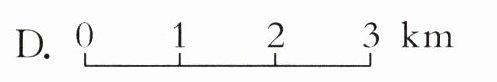
答案：2. C 【提示】比例尺后项最小的，表示实际距离最短。
3. 如果$x$的5倍与$y$的3倍的比是$1:2$，那么$x$与$y$的比是(
A.$3:10$
B.$10:3$
C.$3:5$
D.$5:3$
A
)。A.$3:10$
B.$10:3$
C.$3:5$
D.$5:3$
答案：3. A 【提示】先写出比例式是5x:3y=1:2，再化简求出x与y的比。
4. 下面四幅地图的图幅大小相同，把比例尺按由大到小的顺序排列，正确的是(
①南京市鼓楼区地图 ②中国地图 ③南京市地图 ④江苏省地图
A.①③④②
B.②①④③
C.③④①②
D.②④③①
A
)。①南京市鼓楼区地图 ②中国地图 ③南京市地图 ④江苏省地图
A.①③④②
B.②①④③
C.③④①②
D.②④③①
答案：4. A 【提示】比例尺越大，表示的实际范围越小；比例尺越小，表示的实际范围越大。本题需比较四幅地图表示的实际范围大小，再按比例尺由大到小排序。