一、填一填。(每空2分,共40分)
1. 新情境 世界乒乓球锦标赛 在2025年多哈世界乒乓球锦标赛上,我国乒乓球队以4枚金牌、1枚银牌和2枚铜牌的辉煌战绩结束了本次征程。某工厂生产一批世乒赛纪念乒乓球,每天的产量和生产的天数如下表:
(1)表中(
(2)如果每天生产150个乒乓球,那么这批乒乓球要生产(
(3)这批乒乓球一共有(
1. 新情境 世界乒乓球锦标赛 在2025年多哈世界乒乓球锦标赛上,我国乒乓球队以4枚金牌、1枚银牌和2枚铜牌的辉煌战绩结束了本次征程。某工厂生产一批世乒赛纪念乒乓球,每天的产量和生产的天数如下表:

(1)表中(
每天的产量
)和(生产的天数
)是两个相关联的量。(2)如果每天生产150个乒乓球,那么这批乒乓球要生产(
40
)天;如果每天生产500个乒乓球,那么这批乒乓球要生产(12
)天。(3)这批乒乓球一共有(
6000
)个,也就是每天的产量和生产的天数的积一定,所以(每天的产量
)和(生产的天数
)成(反
)比例。答案:1. (1) 每天的产量 生产的天数
【提示】表中每天的产量和生产的天数是两个相关联的量。
(2) 40 12 【提示】这批乒乓球共有 $ 120 × 50 = 6000 $ (个)。每天生产 150 个,需生产 $ 6000 ÷ 150 = 40 $ (天);每天生产 500 个,需生产 $ 6000 ÷ 500 = 12 $ (天)。
(3) 6000 每天的产量 生产的天数 反
【提示】这批乒乓球共 6000 个,即每天的产量和生产的天数的积为定值,因此它们成反比例。
【提示】表中每天的产量和生产的天数是两个相关联的量。
(2) 40 12 【提示】这批乒乓球共有 $ 120 × 50 = 6000 $ (个)。每天生产 150 个,需生产 $ 6000 ÷ 150 = 40 $ (天);每天生产 500 个,需生产 $ 6000 ÷ 500 = 12 $ (天)。
(3) 6000 每天的产量 生产的天数 反
【提示】这批乒乓球共 6000 个,即每天的产量和生产的天数的积为定值,因此它们成反比例。
2. 如果$\frac{1}{4}x=\frac{1}{2}y$($x$、$y$均不为0),那么$x:y=$(
2
):(1
),$x$和$y$成(正
)比例。答案:
2. 2 1 正 【提示】根据比例的基本性质可得 $ x : y = 1 : 2 $,因为 $ x : y $ 的比值是 $ \frac{1}{2} $ (定值),所以 $ x $ 和 $ y $ 成正比例。
2. 2 1 正 【提示】根据比例的基本性质可得 $ x : y = 1 : 2 $,因为 $ x : y $ 的比值是 $ \frac{1}{2} $ (定值),所以 $ x $ 和 $ y $ 成正比例。
3. 跨学科 立竿见影 用数学的眼光来看成语“立竿见影”,是应用了本学期所学的(
比例
)知识,即同一时间、同一地点,竹竿的高度和影长成(正
)比例关系。答案:
3. 比例 正 【提示】“立竿见影”这个成语中,竹竿的高度和影长之间的关系可以用比例的知识来解释。在同一时间、同一地点,竹竿的高度和影长是成正比例关系的,它们的比值不变。
3. 比例 正 【提示】“立竿见影”这个成语中,竹竿的高度和影长之间的关系可以用比例的知识来解释。在同一时间、同一地点,竹竿的高度和影长是成正比例关系的,它们的比值不变。
4. 左下图中的每个钩码以及增加的钩码都一样重,杠杆的刻度均匀。(填“左”或“右”)
(1)两边各拿掉一个钩码,杠杆的(
(2)把左边的2个钩码向左移动1个刻度,把右边的3个钩码向右移动1个刻度,杠杆的(
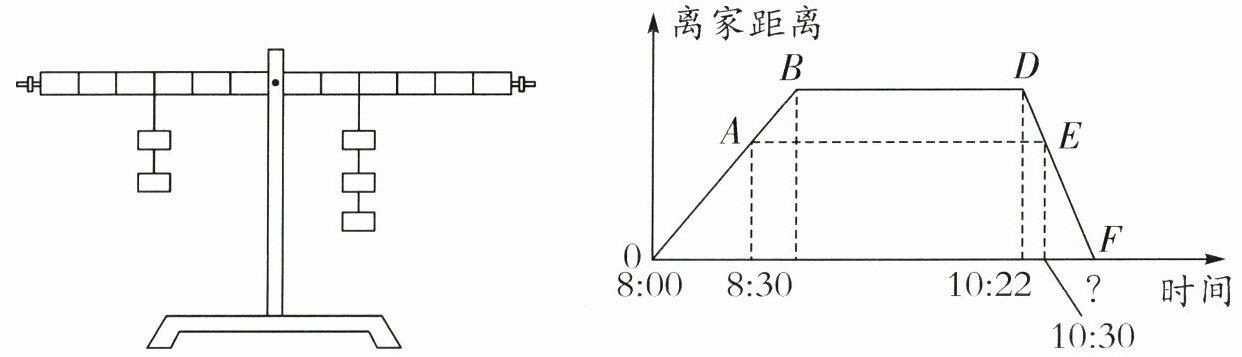
(1)两边各拿掉一个钩码,杠杆的(
右
)边会向下倾斜。两边各增加一个钩码,杠杆的(左
)边会向下倾斜。(2)把左边的2个钩码向左移动1个刻度,把右边的3个钩码向右移动1个刻度,杠杆的(
右
)边会向下倾斜。
答案:
4. (1) 右 左 (2) 右 【提示】杠杆平衡,左边钩码数 $ × $ 刻度数 $ = $ 右边钩码数 $ × $ 刻度数。(1) 两边各拿掉一个钩码,左侧 $ = 1 × 3 = 3 $,右侧 $ = 2 × 2 = 4 $,左侧 $ < $ 右侧,杠杆的右边会向下倾斜。两边各增加一个钩码,左侧 $ = 3 × 3 = 9 $,右侧 $ = 4 × 2 = 8 $,左侧 $ > $ 右侧,杠杆的左边会向下倾斜。(2) 移动后,左侧 $ = 2 × 4 = 8 $,右侧 $ = 3 × 3 = 9 $,左侧 $ < $ 右侧,杠杆的右边会向下倾斜。
4. (1) 右 左 (2) 右 【提示】杠杆平衡,左边钩码数 $ × $ 刻度数 $ = $ 右边钩码数 $ × $ 刻度数。(1) 两边各拿掉一个钩码,左侧 $ = 1 × 3 = 3 $,右侧 $ = 2 × 2 = 4 $,左侧 $ < $ 右侧,杠杆的右边会向下倾斜。两边各增加一个钩码,左侧 $ = 3 × 3 = 9 $,右侧 $ = 4 × 2 = 8 $,左侧 $ > $ 右侧,杠杆的左边会向下倾斜。(2) 移动后,左侧 $ = 2 × 4 = 8 $,右侧 $ = 3 × 3 = 9 $,左侧 $ < $ 右侧,杠杆的右边会向下倾斜。
5. 如右上图,乐乐8:00从家出发去图书馆,10:22回家,已知他去图书馆与回家的速度之比为4:5,他在图书馆待了(
1
)小时(42
)分钟,他到家的时间是(10 : 54
)。答案:
5. 1 42 $ 10 : 54 $ 【提示】10 时 30 分 $ - $ 10 时 22 分 $ = 8 $ 分钟,$ 8 ÷ 4 × 5 = 10 $ (分钟),8 时 30 分 $ + 10 $ 分钟 $ = 8 $ 时 40 分,10 时 22 分 $ - 8 $ 时 40 分 $ = 1 $ 小时 42 分钟;8 时 40 分 $ - 8 $ 时 $ = 40 $ 分钟,$ 40 ÷ 5 × 4 = 32 $ (分钟),10 时 22 分 $ + 32 $ 分钟 $ = 10 $ 时 54 分,路程一定时,速度与时间成反比例。
5. 1 42 $ 10 : 54 $ 【提示】10 时 30 分 $ - $ 10 时 22 分 $ = 8 $ 分钟,$ 8 ÷ 4 × 5 = 10 $ (分钟),8 时 30 分 $ + 10 $ 分钟 $ = 8 $ 时 40 分,10 时 22 分 $ - 8 $ 时 40 分 $ = 1 $ 小时 42 分钟;8 时 40 分 $ - 8 $ 时 $ = 40 $ 分钟,$ 40 ÷ 5 × 4 = 32 $ (分钟),10 时 22 分 $ + 32 $ 分钟 $ = 10 $ 时 54 分,路程一定时,速度与时间成反比例。
6. 如图,一个大长方形被两条线段$AB$、$CD$分成四个部分,其中三部分的面积分别为4平方分米、2平方分米、8平方分米,且第四部分是一个正方形,则涂色部分的面积为(
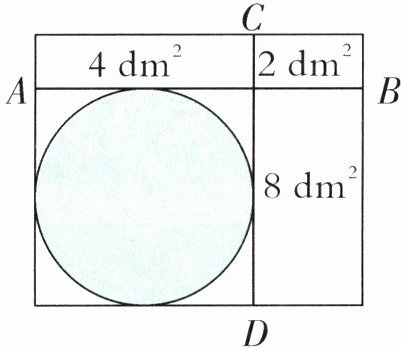
12.56
)平方分米。
答案:
6. 12.56 【提示】设第四部分的正方形面积为 $ x $ 平方分米,可列方程 $ 4 : x = 2 : 8 $,解得 $ x = 16 $。因为 $ 4 × 4 = 16 $,所以第四部分正方形的边长是 4 分米,则涂色部分为直径是 4 分米的圆,根据圆的面积计算公式即可求出涂色部分的面积。
6. 12.56 【提示】设第四部分的正方形面积为 $ x $ 平方分米,可列方程 $ 4 : x = 2 : 8 $,解得 $ x = 16 $。因为 $ 4 × 4 = 16 $,所以第四部分正方形的边长是 4 分米,则涂色部分为直径是 4 分米的圆,根据圆的面积计算公式即可求出涂色部分的面积。