10. (10 分)解不等式 $ \frac{x + 1}{3} - \frac{x - 1}{2} ≤ 1 $,并把它的解集在数轴上表示出来,写出符合条件的 $ x $ 的非正整数解.
答案:
10. 解:去分母,得 $2(x + 1)-3(x - 1)≤6$,
去括号,得 $2x + 2-3x + 3≤6$,
移项、合并同类项,得 $-x≤1$,
两边都除以 $-1$,得 $x≥ - 1$.
其解集在数轴上表示如答图,由图可知符合条件的 $x$ 的非正整数解为 $-1,0$.

10. 解:去分母,得 $2(x + 1)-3(x - 1)≤6$,
去括号,得 $2x + 2-3x + 3≤6$,
移项、合并同类项,得 $-x≤1$,
两边都除以 $-1$,得 $x≥ - 1$.
其解集在数轴上表示如答图,由图可知符合条件的 $x$ 的非正整数解为 $-1,0$.

11. (10 分)已知 $ x - 2y = 3 $,$ x^2 - 2xy + 4y^2 = 13 $. 求下列各式的值:
(1) $ xy $;
(2) $ x^2y - 2xy^2 $.
(1) $ xy $;
(2) $ x^2y - 2xy^2 $.
答案:11. 解:(1)因为 $x - 2y = 3,x^{2}-2xy + 4y^{2}=13$,所以 $(x - 2y)^{2}+2xy = 13$,所以 $3^{2}+2xy = 13$,所以 $xy = 2$.
(2)因为 $x - 2y = 3,xy = 2$,所以 $x^{2}y-2xy^{2}=xy(x - 2y)=2×3 = 6$.
(2)因为 $x - 2y = 3,xy = 2$,所以 $x^{2}y-2xy^{2}=xy(x - 2y)=2×3 = 6$.
12. (15 分)某火车货运站现有甲种货物 1530 吨,乙种货物 1150 吨,某公司将安排一列火车将这批货物运往上海,这列火车可挂 $ A,B $ 两种不同型号的货厢 50 节.
(1)已知甲种货物 35 吨和乙种货物 15 吨可装满一节 $ A $ 型货厢,甲种货物 25 吨和乙种货物 35 吨可装满一节 $ B $ 型货厢,运输这批货物有几种安排货厢的方案?
(2)若一节 $ A $ 型货厢的运费是 0.5 万元,一节 $ B $ 型货厢的运费是 0.8 万元,如何安排运输方案,才能使得运费最少? 并求出最少运费.
(1)已知甲种货物 35 吨和乙种货物 15 吨可装满一节 $ A $ 型货厢,甲种货物 25 吨和乙种货物 35 吨可装满一节 $ B $ 型货厢,运输这批货物有几种安排货厢的方案?
(2)若一节 $ A $ 型货厢的运费是 0.5 万元,一节 $ B $ 型货厢的运费是 0.8 万元,如何安排运输方案,才能使得运费最少? 并求出最少运费.
答案:12. 解:(1)设安排 $A$ 型货厢 $x$ 节,则安排 $B$ 型货厢 $(50 - x)$ 节,
根据题意,得 $\begin{cases}35x + 25(50 - x)≥1530,\\15x + 35(50 - x)≥1150,\end{cases}$
解得 $28≤ x≤30$. 因为 $x$ 为整数,所以 $x$ 可取 $28$, $29,30$.
所以运输这批货物有 $3$ 种安排货厢的方案:
方案一:安排 $28$ 节 $A$ 型货厢,$22$ 节 $B$ 型货厢.
方案二:安排 $29$ 节 $A$ 型货厢,$21$ 节 $B$ 型货厢.
方案三:安排 $30$ 节 $A$ 型货厢,$20$ 节 $B$ 型货厢.
(2)按方案一,运费为 $28×0.5 + 22×0.8 = 31.6$ (万元).
按方案二,运费为 $29×0.5 + 21×0.8 = 31.3$ (万元).
按方案三,运费为 $30×0.5 + 20×0.8 = 31$ (万元).
因为 $31<31.3<31.6$,
所以按方案三运输运费最少,最少运费为 $31$ 万元.
根据题意,得 $\begin{cases}35x + 25(50 - x)≥1530,\\15x + 35(50 - x)≥1150,\end{cases}$
解得 $28≤ x≤30$. 因为 $x$ 为整数,所以 $x$ 可取 $28$, $29,30$.
所以运输这批货物有 $3$ 种安排货厢的方案:
方案一:安排 $28$ 节 $A$ 型货厢,$22$ 节 $B$ 型货厢.
方案二:安排 $29$ 节 $A$ 型货厢,$21$ 节 $B$ 型货厢.
方案三:安排 $30$ 节 $A$ 型货厢,$20$ 节 $B$ 型货厢.
(2)按方案一,运费为 $28×0.5 + 22×0.8 = 31.6$ (万元).
按方案二,运费为 $29×0.5 + 21×0.8 = 31.3$ (万元).
按方案三,运费为 $30×0.5 + 20×0.8 = 31$ (万元).
因为 $31<31.3<31.6$,
所以按方案三运输运费最少,最少运费为 $31$ 万元.
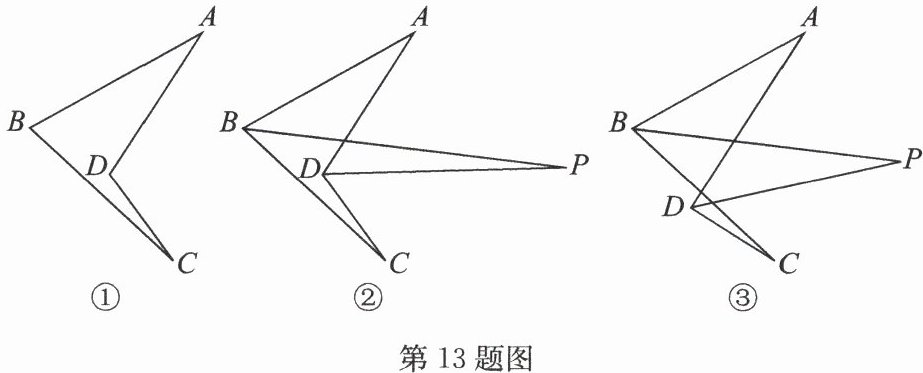
13. (16 分)已知 $ D $ 是 $ ∠ ABC $ 所在平面内一点,连接 $ AD,CD $.
(1)如图①,若 $ ∠ A = 28° $,$ ∠ B = 72° $,$ ∠ C = 11° $,求 $ ∠ ADC $ 的度数;
(2)如图②,若 $ BP $ 平分 $ ∠ ABC $,$ DP $ 平分 $ ∠ ADC $,探究 $ ∠ A $,$ ∠ P $,$ ∠ C $ 的数量关系并证明;
(3)如图③,在(2)的条件下,将点 $ D $ 移至 $ ∠ ABC $ 的外部,其他条件不变,探究 $ ∠ A $,$ ∠ P $,$ ∠ C $ 的数量关系并证明.
(1)如图①,若 $ ∠ A = 28° $,$ ∠ B = 72° $,$ ∠ C = 11° $,求 $ ∠ ADC $ 的度数;
(2)如图②,若 $ BP $ 平分 $ ∠ ABC $,$ DP $ 平分 $ ∠ ADC $,探究 $ ∠ A $,$ ∠ P $,$ ∠ C $ 的数量关系并证明;
(3)如图③,在(2)的条件下,将点 $ D $ 移至 $ ∠ ABC $ 的外部,其他条件不变,探究 $ ∠ A $,$ ∠ P $,$ ∠ C $ 的数量关系并证明.

答案:
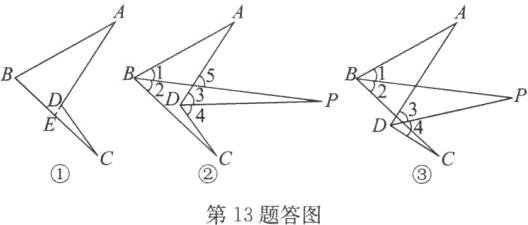
13. 解:(1)如答图①,延长 $AD$ 交 $BC$ 于点 $E$. 在 $△ ABE$ 中,$∠ AEC=∠ A+∠ B = 28^{\circ}+72^{\circ}=100^{\circ}$,在 $△ DEC$ 中,$∠ ADC=∠ AEC+∠ C = 100^{\circ}+11^{\circ}=111^{\circ}$.
(2) $∠ A-∠ C = 2∠ P$.
证明:如答图②,$∠5=∠ A+∠1,∠5=∠ P+∠3$,
所以 $∠ A+∠1=∠ P+∠3$.
因为 $BP$ 平分 $∠ ABC$,$DP$ 平分 $∠ ADC$,
所以 $∠1=∠2,∠3=∠4$,
所以 $∠ A+∠2=∠ P+∠4$.
由(1)知 $∠4=∠2+∠ P+∠ C$,
所以 $∠ A+∠2=∠ P+∠2+∠ P+∠ C$,
所以 $∠ A-∠ C = 2∠ P$.
(3) $∠ A+∠ C = 2∠ P$.
证明:如答图③,
因为 $∠ A+∠1=∠ P+∠3,∠ C+∠4=∠ P+∠2$,
所以 $∠ A+∠ C+∠1+∠4 = 2∠ P+∠2+∠3$.
因为 $BP$ 平分 $∠ ABC$,$DP$ 平分 $∠ ADC$,
所以 $∠1=∠2,∠3=∠4$,
所以 $∠1+∠4=∠2+∠3$,所以 $∠ A+∠ C = 2∠ P$.
13. 解:(1)如答图①,延长 $AD$ 交 $BC$ 于点 $E$. 在 $△ ABE$ 中,$∠ AEC=∠ A+∠ B = 28^{\circ}+72^{\circ}=100^{\circ}$,在 $△ DEC$ 中,$∠ ADC=∠ AEC+∠ C = 100^{\circ}+11^{\circ}=111^{\circ}$.
(2) $∠ A-∠ C = 2∠ P$.
证明:如答图②,$∠5=∠ A+∠1,∠5=∠ P+∠3$,
所以 $∠ A+∠1=∠ P+∠3$.
因为 $BP$ 平分 $∠ ABC$,$DP$ 平分 $∠ ADC$,
所以 $∠1=∠2,∠3=∠4$,
所以 $∠ A+∠2=∠ P+∠4$.
由(1)知 $∠4=∠2+∠ P+∠ C$,
所以 $∠ A+∠2=∠ P+∠2+∠ P+∠ C$,
所以 $∠ A-∠ C = 2∠ P$.
(3) $∠ A+∠ C = 2∠ P$.
证明:如答图③,
因为 $∠ A+∠1=∠ P+∠3,∠ C+∠4=∠ P+∠2$,
所以 $∠ A+∠ C+∠1+∠4 = 2∠ P+∠2+∠3$.
因为 $BP$ 平分 $∠ ABC$,$DP$ 平分 $∠ ADC$,
所以 $∠1=∠2,∠3=∠4$,
所以 $∠1+∠4=∠2+∠3$,所以 $∠ A+∠ C = 2∠ P$.
