1. (2024·巴中)下列运算正确的是 (
A.$3a + b = 3ab$
B.$a^3 · a^2 = a^5$
C.$a^8 ÷ a^2 = a^4(a ≠ 0)$
D.$(a - b)^2 = a^2 - b^2$
B
)A.$3a + b = 3ab$
B.$a^3 · a^2 = a^5$
C.$a^8 ÷ a^2 = a^4(a ≠ 0)$
D.$(a - b)^2 = a^2 - b^2$
答案:1. B
2. 下列四个垃圾分类标识中,其文字上方的图案属于轴对称图形的是 (

C
)
答案:2. C
3. (2025·宿迁模拟)2025年4月23日是第30个“世界读书日”,宿迁市新华书店特推出“倡导全民阅读,构建文明社会”的主题促销活动,某种标价$a$元/本的畅销书,每本进价是标价的五折,书店要想不亏本,必须保证每本书的利润率不低于30%,那么书店对该畅销书最多可打 (
A.五折
B.六折
C.六五折
D.不确定
C
)A.五折
B.六折
C.六五折
D.不确定
答案:3. C
解析:
设书店对该畅销书打$x$折。
进价为标价的五折,即进价为$0.5a$元。
售价为标价打$x$折,即售价为$a×\frac{x}{10}$元。
利润率不低于$30\%$,则利润$≥0.5a×30\%$,即售价$-$进价$≥0.15a$。
可得不等式:$a×\frac{x}{10}-0.5a≥0.15a$
两边同时除以$a$($a>0$):$\frac{x}{10}-0.5≥0.15$
$\frac{x}{10}≥0.65$
$x≥6.5$
所以最多可打六五折。
C
进价为标价的五折,即进价为$0.5a$元。
售价为标价打$x$折,即售价为$a×\frac{x}{10}$元。
利润率不低于$30\%$,则利润$≥0.5a×30\%$,即售价$-$进价$≥0.15a$。
可得不等式:$a×\frac{x}{10}-0.5a≥0.15a$
两边同时除以$a$($a>0$):$\frac{x}{10}-0.5≥0.15$
$\frac{x}{10}≥0.65$
$x≥6.5$
所以最多可打六五折。
C
4. (2024·张家港期末)若关于$x$,$y$的二元一次方程组$\begin{cases}x + y = 5k \\ x - y = 9k\end{cases}$的解也是二元一次方程$x + 3y = 1$的解,则$k$的值为 ( )
A.1
B.2
C.3
D.4
A.1
B.2
C.3
D.4
答案:4. A
解析:
解:解方程组$\begin{cases}x + y = 5k \\ x - y = 9k\end{cases}$,
两式相加得:$2x = 14k$,解得$x = 7k$,
将$x = 7k$代入$x + y = 5k$,得$7k + y = 5k$,解得$y = -2k$,
把$x = 7k$,$y = -2k$代入$x + 3y = 1$,得$7k + 3×(-2k) = 1$,
即$7k - 6k = 1$,解得$k = 1$。
A
两式相加得:$2x = 14k$,解得$x = 7k$,
将$x = 7k$代入$x + y = 5k$,得$7k + y = 5k$,解得$y = -2k$,
把$x = 7k$,$y = -2k$代入$x + 3y = 1$,得$7k + 3×(-2k) = 1$,
即$7k - 6k = 1$,解得$k = 1$。
A
5. (2024·湖滨新区期末)已知$a - 2b = 5$,$(a - 3)(2b + 3) = 10$,则$a^2 - 7ab + 4b^2$的值为(
A.2
B.19
C.25
D.31
B
)A.2
B.19
C.25
D.31
答案:5. B
解析:
已知$a - 2b = 5$,设$a = 2b + 5$。
将$a = 2b + 5$代入$(a - 3)(2b + 3) = 10$,得:
$\begin{aligned}(2b + 5 - 3)(2b + 3)&=10\\(2b + 2)(2b + 3)&=10\\4b^2 + 6b + 4b + 6&=10\\4b^2 + 10b + 6 - 10&=0\\4b^2 + 10b - 4&=0\\2b^2 + 5b - 2&=0\\2b^2 + 5b&=2\end{aligned}$
$a^2 - 7ab + 4b^2=(a - 2b)^2 - 3ab$,因为$a - 2b = 5$,所以$(a - 2b)^2 = 25$。
$ab=(2b + 5)b = 2b^2 + 5b = 2$,则$3ab = 6$。
所以$a^2 - 7ab + 4b^2=25 - 6 = 19$。
19
将$a = 2b + 5$代入$(a - 3)(2b + 3) = 10$,得:
$\begin{aligned}(2b + 5 - 3)(2b + 3)&=10\\(2b + 2)(2b + 3)&=10\\4b^2 + 6b + 4b + 6&=10\\4b^2 + 10b + 6 - 10&=0\\4b^2 + 10b - 4&=0\\2b^2 + 5b - 2&=0\\2b^2 + 5b&=2\end{aligned}$
$a^2 - 7ab + 4b^2=(a - 2b)^2 - 3ab$,因为$a - 2b = 5$,所以$(a - 2b)^2 = 25$。
$ab=(2b + 5)b = 2b^2 + 5b = 2$,则$3ab = 6$。
所以$a^2 - 7ab + 4b^2=25 - 6 = 19$。
19
6. 命题“对顶角相等”的逆命题是
相等的两个角是对顶角
.答案:6. 相等的两个角是对顶角
7. (2024·天宁区期末)关于$x$的不等式组$\begin{cases}x - 1 > 0 \\ x - 2 ≤ m\end{cases}$有且只有两个整数解,则$m$的取值范围是 ______ .
答案:7. $1 ≤ m < 2 $
解析:
解不等式组:
解$x - 1 > 0$,得$x > 1$;
解$x - 2 ≤ m$,得$x ≤ m + 2$。
所以不等式组的解集为$1 < x ≤ m + 2$。
因为不等式组有且只有两个整数解,即2,3,
所以$3 ≤ m + 2 < 4$,
解得$1 ≤ m < 2$。
$1 ≤ m < 2$
解$x - 1 > 0$,得$x > 1$;
解$x - 2 ≤ m$,得$x ≤ m + 2$。
所以不等式组的解集为$1 < x ≤ m + 2$。
因为不等式组有且只有两个整数解,即2,3,
所以$3 ≤ m + 2 < 4$,
解得$1 ≤ m < 2$。
$1 ≤ m < 2$
8. (2024·宿豫区模拟)若$a = 2 - b$,$ab = t - 1$,则$(a^2 - 1)(b^2 - 1)$的最小值为
$ -4 $
.答案:8. $ -4 $
解析:
解:因为$a = 2 - b$,所以$a + b = 2$。
$(a^2 - 1)(b^2 - 1)$
$=a^2b^2 - a^2 - b^2 + 1$
$=(ab)^2 - (a^2 + b^2) + 1$
$=(ab)^2 - [(a + b)^2 - 2ab] + 1$
因为$ab = t - 1$,$a + b = 2$,所以原式$=(t - 1)^2 - (2^2 - 2(t - 1)) + 1$
$=t^2 - 2t + 1 - (4 - 2t + 2) + 1$
$=t^2 - 2t + 1 - 6 + 2t + 1$
$=t^2 - 4$
因为$t^2 ≥ 0$,所以$t^2 - 4 ≥ -4$,即$(a^2 - 1)(b^2 - 1)$的最小值为$-4$。
$-4$
$(a^2 - 1)(b^2 - 1)$
$=a^2b^2 - a^2 - b^2 + 1$
$=(ab)^2 - (a^2 + b^2) + 1$
$=(ab)^2 - [(a + b)^2 - 2ab] + 1$
因为$ab = t - 1$,$a + b = 2$,所以原式$=(t - 1)^2 - (2^2 - 2(t - 1)) + 1$
$=t^2 - 2t + 1 - (4 - 2t + 2) + 1$
$=t^2 - 2t + 1 - 6 + 2t + 1$
$=t^2 - 4$
因为$t^2 ≥ 0$,所以$t^2 - 4 ≥ -4$,即$(a^2 - 1)(b^2 - 1)$的最小值为$-4$。
$-4$
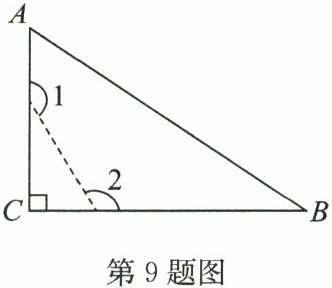
9. (2025·宿城区期中)如图,在直角$△ ABC$中,$∠ C = 90°$,沿图中虚线剪去$∠ C$,则$∠ 1 + ∠ 2 = $
270
°.
答案:9. 270
解析:
解:在直角$△ABC$中,$∠C = 90°$,则$∠A + ∠B = 180° - ∠C = 90°$。
沿虚线剪去$∠C$后,形成一个四边形,四边形内角和为$360°$。
$∠1$和$∠2$是四边形的两个外角,其邻补角分别为$180° - ∠1$和$180° - ∠2$。
所以$(180° - ∠1) + (180° - ∠2) + ∠A + ∠B = 360°$,即$360° - (∠1 + ∠2) + 90° = 360°$,解得$∠1 + ∠2 = 270°$。
270
沿虚线剪去$∠C$后,形成一个四边形,四边形内角和为$360°$。
$∠1$和$∠2$是四边形的两个外角,其邻补角分别为$180° - ∠1$和$180° - ∠2$。
所以$(180° - ∠1) + (180° - ∠2) + ∠A + ∠B = 360°$,即$360° - (∠1 + ∠2) + 90° = 360°$,解得$∠1 + ∠2 = 270°$。
270