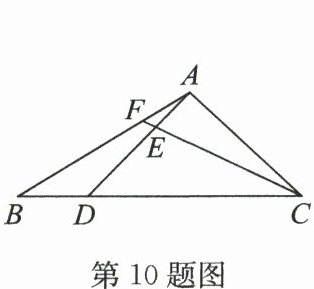
10. (2025·钟吾初中期末)如图,$△ ABC$的面积为12,$DE = 2AE$,$CD = 3BD$,则$△ AEF$的面积等于
$ \frac { 3 } { 1 1 } $
.
答案:10. $ \frac { 3 } { 1 1 } $
解析:
解:设$△AEF$的面积为$x$。
因为$CD = 3BD$,$△ABC$的面积为12,所以$S_{△ABD}=\frac{1}{4}S_{△ABC}=3$,$S_{△ACD}=\frac{3}{4}S_{△ABC}=9$。
设$AE = a$,则$DE = 2a$,$AD = 3a$。
连接$DF$,设$S_{△DEF}=2x$(因为$DE = 2AE$,高相同,面积比等于底之比)。
设$S_{△BDF}=y$,则$S_{△CDF}=3y$(因为$CD = 3BD$,高相同,面积比等于底之比)。
在$△ABD$中,$S_{△ABD}=S_{△AEF}+S_{△DEF}+S_{△BDF}=x + 2x + y=3x + y=3$。
在$△ADC$中,$S_{△ADC}=S_{△AFC}+S_{△DFC}$,$S_{△AFC}=S_{△AFD}+S_{△DFC}$,$S_{△AFD}=x + 2x=3x$,所以$S_{△AFC}=3x + 3y$,则$3x + 3y + 3y=9$,即$3x + 6y=9$,化简得$x + 2y=3$。
联立方程组$\begin{cases}3x + y=3\\x + 2y=3\end{cases}$,解得$x=\frac{3}{11}$。
故$△AEF$的面积等于$\frac{3}{11}$。
因为$CD = 3BD$,$△ABC$的面积为12,所以$S_{△ABD}=\frac{1}{4}S_{△ABC}=3$,$S_{△ACD}=\frac{3}{4}S_{△ABC}=9$。
设$AE = a$,则$DE = 2a$,$AD = 3a$。
连接$DF$,设$S_{△DEF}=2x$(因为$DE = 2AE$,高相同,面积比等于底之比)。
设$S_{△BDF}=y$,则$S_{△CDF}=3y$(因为$CD = 3BD$,高相同,面积比等于底之比)。
在$△ABD$中,$S_{△ABD}=S_{△AEF}+S_{△DEF}+S_{△BDF}=x + 2x + y=3x + y=3$。
在$△ADC$中,$S_{△ADC}=S_{△AFC}+S_{△DFC}$,$S_{△AFC}=S_{△AFD}+S_{△DFC}$,$S_{△AFD}=x + 2x=3x$,所以$S_{△AFC}=3x + 3y$,则$3x + 3y + 3y=9$,即$3x + 6y=9$,化简得$x + 2y=3$。
联立方程组$\begin{cases}3x + y=3\\x + 2y=3\end{cases}$,解得$x=\frac{3}{11}$。
故$△AEF$的面积等于$\frac{3}{11}$。
11. (12分)计算:
(1)$a^3 · a^5 - (a^4)^2 + a^{10} ÷ a^2$;
(2)$(x + y)(x - y) - (x - y)^2$.
(1)$a^3 · a^5 - (a^4)^2 + a^{10} ÷ a^2$;
(2)$(x + y)(x - y) - (x - y)^2$.
答案:11. 解: (1) 原式 $ = a ^ { 8 } - a ^ { 8 } + a ^ { 8 } = a ^ { 8 } $.
(2) 原式 $ = x ^ { 2 } - y ^ { 2 } - ( x ^ { 2 } - 2 x y + y ^ { 2 } ) = x ^ { 2 } - y ^ { 2 } - x ^ { 2 } + 2 x y - y ^ { 2 } = 2 x y - 2 y ^ { 2 } $.
(2) 原式 $ = x ^ { 2 } - y ^ { 2 } - ( x ^ { 2 } - 2 x y + y ^ { 2 } ) = x ^ { 2 } - y ^ { 2 } - x ^ { 2 } + 2 x y - y ^ { 2 } = 2 x y - 2 y ^ { 2 } $.
12. (12分)解不等式组$\begin{cases}3x - 1 ≥ x + 1 \\ x + 4 < 4x - 2\end{cases}$,并直接写出它的最小整数解.
答案:12. 解: $ \{ \begin{array} { l } { 3 x - 1 ≥ x + 1, \textcircled { 1 } } \\ { x + 4 < 4 x - 2, \textcircled { 2 } } \end{array} $
解不等式①, 得 $ x ≥ 1 $, 解不等式②, 得 $ x > 2 $,
所以原不等式组的解集为 $ x > 2 $, 它的最小整数解为 3.
解不等式①, 得 $ x ≥ 1 $, 解不等式②, 得 $ x > 2 $,
所以原不等式组的解集为 $ x > 2 $, 它的最小整数解为 3.
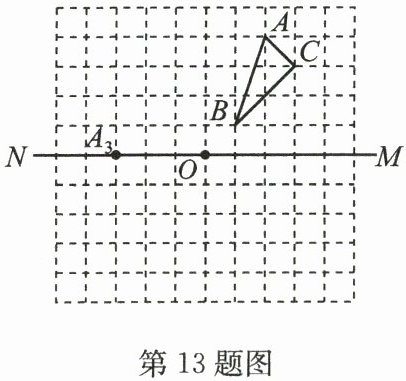
13. (12分)在如图所示的方格纸中,$△ ABC$的顶点都在边长为1个单位长度的小正方形的顶点上. 按下列要求画图:
(1)画出$△ ABC$关于直线$MN$对称的$△ A_1B_1C_1$;
(2)绕点$B$顺时针旋转$△ ABC$,使得点$A$的对应点落在射线$OM$上,旋转后的三角形为$△ A_2BC_2$;
(3)平移$△ ABC$,得到$△ A_3B_3C_3$,其中点$A$和点$A_3$对应;
(4)将$△ ABC$绕点$O$旋转$180°$,得到$△ A_4B_4C_4$.
(1)画出$△ ABC$关于直线$MN$对称的$△ A_1B_1C_1$;
(2)绕点$B$顺时针旋转$△ ABC$,使得点$A$的对应点落在射线$OM$上,旋转后的三角形为$△ A_2BC_2$;
(3)平移$△ ABC$,得到$△ A_3B_3C_3$,其中点$A$和点$A_3$对应;
(4)将$△ ABC$绕点$O$旋转$180°$,得到$△ A_4B_4C_4$.

答案:
13. 解: (1)(2)(3)(4) 如答图所示.
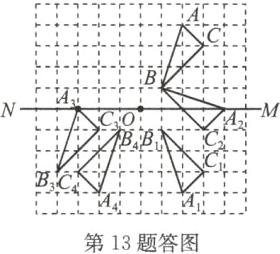
13. 解: (1)(2)(3)(4) 如答图所示.

14. (14分)(2024·宿豫区期末)用2辆A型车和3辆B型车载满货物一次可运货18吨;用1辆A型车和2辆B型车载满货物一次可运货11吨. 某物流公司现有27吨货物,计划两种车型都要租,其中A型车$a$辆,B型车$b$辆,一次运完,且恰好每辆车都载满货物.
(1)用1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨?
(2)若A型车每辆需租金100元/次,B型车每辆需租金120元/次. 请你帮物流公司设计租车方案,并求出此时的租车费用.
(1)用1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨?
(2)若A型车每辆需租金100元/次,B型车每辆需租金120元/次. 请你帮物流公司设计租车方案,并求出此时的租车费用.
答案:14. 解: (1) 设用 1 辆 A 型车和 1 辆车 B 型车都载满货物一次可分别运货 $ x $ 吨, $ y $ 吨, 根据题意, 得
$ \{ \begin{array} { l } { 2 x + 3 y = 1 8 }, \\ { x + 2 y = 1 1 }, \end{array} $ 解得 $ \{ \begin{array} { l } { x = 3 }, \\ { y = 4 }. \end{array} $
答: 用 1 辆 A 型车和 1 辆车 B 型车都载满货物一次可分别运货 3 吨, 4 吨.
(2) 由题意, 得 $ 3 a + 4 b = 2 7 $, $ a = 9 - \frac { 4 } { 3 } b $,
因为 $ a $, $ b $ 都是正整数, 所以当 $ b = 3 $ 时, $ a = 5 $;
当 $ b = 6 $ 时, $ a = 1 $.
所以物流公司共有 2 种租车方案: 租用 5 辆 A 型车, 3 辆 B 型车, 租车费用为 $ 5 × 1 0 0 + 3 × 1 2 0 = 8 6 0 $(元);
租用 1 辆 A 型车, 6 辆 B 型车, 租车费用为 $ 1 × 1 0 0 + 6 × 1 2 0 = 8 2 0 $(元).
$ \{ \begin{array} { l } { 2 x + 3 y = 1 8 }, \\ { x + 2 y = 1 1 }, \end{array} $ 解得 $ \{ \begin{array} { l } { x = 3 }, \\ { y = 4 }. \end{array} $
答: 用 1 辆 A 型车和 1 辆车 B 型车都载满货物一次可分别运货 3 吨, 4 吨.
(2) 由题意, 得 $ 3 a + 4 b = 2 7 $, $ a = 9 - \frac { 4 } { 3 } b $,
因为 $ a $, $ b $ 都是正整数, 所以当 $ b = 3 $ 时, $ a = 5 $;
当 $ b = 6 $ 时, $ a = 1 $.
所以物流公司共有 2 种租车方案: 租用 5 辆 A 型车, 3 辆 B 型车, 租车费用为 $ 5 × 1 0 0 + 3 × 1 2 0 = 8 6 0 $(元);
租用 1 辆 A 型车, 6 辆 B 型车, 租车费用为 $ 1 × 1 0 0 + 6 × 1 2 0 = 8 2 0 $(元).