1. 下列运算正确的是(
A.$ a^{2} · a^{4}=a^{8} $
B.$ (a - 3)^{2}=a^{2}-9 $
C.$ a^{3}+a^{3}=a^{6} $
D.$ (2ab^{2})^{2}=4a^{2}b^{4} $
D
)A.$ a^{2} · a^{4}=a^{8} $
B.$ (a - 3)^{2}=a^{2}-9 $
C.$ a^{3}+a^{3}=a^{6} $
D.$ (2ab^{2})^{2}=4a^{2}b^{4} $
答案:1. D
2. (2025·宿豫区期末)如果$ a < b $,下列各式中正确的是(
A.$ a c^{2}<b c^{2} $
B.$ \frac{1}{a}>\frac{1}{b} $
C.$ -3 a>-3 b $
D.$ \frac{a}{4}>\frac{b}{4} $
C
)A.$ a c^{2}<b c^{2} $
B.$ \frac{1}{a}>\frac{1}{b} $
C.$ -3 a>-3 b $
D.$ \frac{a}{4}>\frac{b}{4} $
答案:2. C
3. 一个多边形的每个内角都等于$ 135^{\circ} $,则这个多边形的边数为(
A.8
B.9
C.10
D.11
A
)A.8
B.9
C.10
D.11
答案:3. A
解析:
设这个多边形的边数为$n$。
因为多边形的内角和公式为$(n - 2)×180^{\circ}$,且每个内角都等于$135^{\circ}$,所以可得方程:
$(n - 2)×180^{\circ} = 135^{\circ}×n$
$180n - 360 = 135n$
$180n - 135n = 360$
$45n = 360$
$n = 8$
A
因为多边形的内角和公式为$(n - 2)×180^{\circ}$,且每个内角都等于$135^{\circ}$,所以可得方程:
$(n - 2)×180^{\circ} = 135^{\circ}×n$
$180n - 360 = 135n$
$180n - 135n = 360$
$45n = 360$
$n = 8$
A
4. 若$ x = 3^{5}, y = 2^{3} $,则$ 6^{15} $用$ x,y $表示为(
A.$ x y $
B.$ x^{15} y^{15} $
C.$ x^{5} y^{3} $
D.$ x^{3} y^{5} $
D
)A.$ x y $
B.$ x^{15} y^{15} $
C.$ x^{5} y^{3} $
D.$ x^{3} y^{5} $
答案:4. D
解析:
因为$x = 3^{5}$,$y = 2^{3}$,所以$6^{15}=(2×3)^{15}=2^{15}×3^{15}$。
又因为$2^{15}=(2^{3})^{5}=y^{5}$,$3^{15}=(3^{5})^{3}=x^{3}$,所以$6^{15}=x^{3}y^{5}$。
D
又因为$2^{15}=(2^{3})^{5}=y^{5}$,$3^{15}=(3^{5})^{3}=x^{3}$,所以$6^{15}=x^{3}y^{5}$。
D
5. 如图,把一张长方形纸条$ ABCD $沿$ EF $折叠,$ C,D $两点分别落在点$ C^{\prime}, D^{\prime} $处.已知$ ∠ D A C = 20^{\circ} $,且$ C^{\prime} D^{\prime} // A C $,则$ ∠ A E F $的度数为(
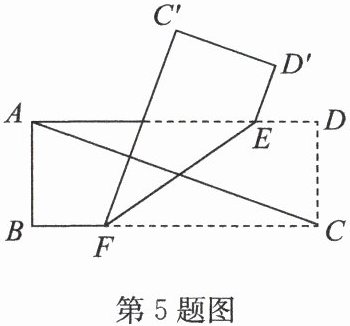
A.$ 20^{\circ} $
B.$ 35^{\circ} $
C.$ 50^{\circ} $
D.$ 70^{\circ} $
B
)
A.$ 20^{\circ} $
B.$ 35^{\circ} $
C.$ 50^{\circ} $
D.$ 70^{\circ} $
答案:5. B
解析:
解:
∵ 四边形 $ABCD$ 是长方形,
∴ $AD // BC$,$∠ ADC = 90°$。
∵ $∠ DAC = 20°$,
∴ $∠ ACD = 90° - 20° = 70°$。
∵ $C'D' // AC$,
∴ $∠ C'EC = ∠ ACD = 70°$(两直线平行,内错角相等)。
由折叠性质,$∠ C'EF = ∠ CEF$,
∴ $∠ CEF = \frac{1}{2} ∠ C'EC = 35°$。
∵ $AD // BC$,
∴ $∠ AEF = ∠ CEF = 35°$(两直线平行,内错角相等)。
答案:B
∵ 四边形 $ABCD$ 是长方形,
∴ $AD // BC$,$∠ ADC = 90°$。
∵ $∠ DAC = 20°$,
∴ $∠ ACD = 90° - 20° = 70°$。
∵ $C'D' // AC$,
∴ $∠ C'EC = ∠ ACD = 70°$(两直线平行,内错角相等)。
由折叠性质,$∠ C'EF = ∠ CEF$,
∴ $∠ CEF = \frac{1}{2} ∠ C'EC = 35°$。
∵ $AD // BC$,
∴ $∠ AEF = ∠ CEF = 35°$(两直线平行,内错角相等)。
答案:B
6. 计算:$ \frac{2022^{2}-2040^{2}-18^{2}}{2040 × 18}= $
-2
.答案:6. -2
解析:
$\begin{aligned}&\frac{2022^{2}-2040^{2}-18^{2}}{2040×18}\\=&\frac{2022^{2}-(2040^{2}+18^{2})}{2040×18}\\=&\frac{2022^{2}-(2040^{2}+2×2040×18 + 18^{2}-2×2040×18)}{2040×18}\\=&\frac{2022^{2}-(2040 + 18)^{2}+2×2040×18}{2040×18}\\=&\frac{2022^{2}-2058^{2}+2×2040×18}{2040×18}\\=&\frac{(2022 - 2058)(2022 + 2058)+2×2040×18}{2040×18}\\=&\frac{(-36)×4080 + 2×2040×18}{2040×18}\\=&\frac{-36×2×2040 + 2×2040×18}{2040×18}\\=&\frac{-72×2040 + 36×2040}{2040×18}\\=&\frac{(-72 + 36)×2040}{2040×18}\\=&\frac{-36×2040}{2040×18}\\=&-2\end{aligned}$
7. (2024·秦淮区期中)如图,在$ △ A B C $中,$ ∠ B A C = 90^{\circ}, A B = 3, A C = 4, B C = 5 $,将$ △ A B C $沿直线$ B C $向右平移2个单位长度得到$ △ D E F $,连接$ A D $.有下列结论:①$ A C // D F, A C = D F $;②$ E D ⊥ D F $;③四边形$ A B F D $的周长是16;④$ A D: E C = 2: 3 $.其中正确的结论是
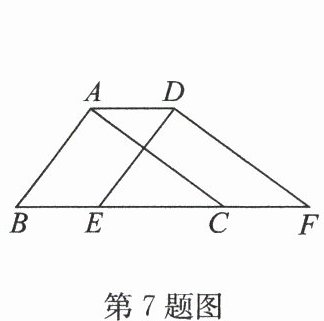
①②③④
. (填序号)
答案:7. ①②③④
解析:
证明:
①
∵△ABC沿直线BC向右平移2个单位长度得到△DEF,
∴AC//DF,AC=DF,故①正确;
②
∵∠BAC=90°,AB=3,AC=4,BC=5,平移得DE=AB=3,DF=AC=4,∠EDF=∠BAC=90°,
∴ED⊥DF,故②正确;
③
∵平移距离为2,
∴AD=CF=2,BF=BC+CF=5+2=7,
四边形ABFD的周长=AB+BF+FD+DA=3+7+4+2=16,故③正确;
④
∵EC=BC-BE=5-2=3,AD=2,
∴AD:EC=2:3,故④正确。
综上,正确的结论是①②③④。
①
∵△ABC沿直线BC向右平移2个单位长度得到△DEF,
∴AC//DF,AC=DF,故①正确;
②
∵∠BAC=90°,AB=3,AC=4,BC=5,平移得DE=AB=3,DF=AC=4,∠EDF=∠BAC=90°,
∴ED⊥DF,故②正确;
③
∵平移距离为2,
∴AD=CF=2,BF=BC+CF=5+2=7,
四边形ABFD的周长=AB+BF+FD+DA=3+7+4+2=16,故③正确;
④
∵EC=BC-BE=5-2=3,AD=2,
∴AD:EC=2:3,故④正确。
综上,正确的结论是①②③④。
8. 命题“同号两数的和一定不是负数”的条件是
两个数同号
,结论是它们的和一定不是负数
.答案:8. 两个数同号 它们的和一定不是负数
9. 若关于$ x $的不等式组$ \{\begin{array}{l} \frac{x - 3}{2} ≥ \frac{2 x + 1}{3}-3, \\ 2 x - m>5 \end{array} $至少有3个整数解,则$ m $的取值范围是 ______ .
答案:9. $ m < 5 $
解析:
解不等式$\frac{x - 3}{2} ≥ \frac{2x + 1}{3}-3$:
去分母,得$3(x - 3) ≥ 2(2x + 1)-18$,
去括号,得$3x - 9 ≥ 4x + 2 - 18$,
移项,得$3x - 4x ≥ 2 - 18 + 9$,
合并同类项,得$-x ≥ -7$,
系数化为$1$,得$x ≤ 7$。
解不等式$2x - m>5$:
移项,得$2x>5 + m$,
系数化为$1$,得$x>\frac{5 + m}{2}$。
所以不等式组的解集为$\frac{5 + m}{2}<x ≤ 7$。
因为不等式组至少有$3$个整数解,即$5$,$6$,$7$,
所以$\frac{5 + m}{2}<5$,
解得$m<5$。
$m<5$
去分母,得$3(x - 3) ≥ 2(2x + 1)-18$,
去括号,得$3x - 9 ≥ 4x + 2 - 18$,
移项,得$3x - 4x ≥ 2 - 18 + 9$,
合并同类项,得$-x ≥ -7$,
系数化为$1$,得$x ≤ 7$。
解不等式$2x - m>5$:
移项,得$2x>5 + m$,
系数化为$1$,得$x>\frac{5 + m}{2}$。
所以不等式组的解集为$\frac{5 + m}{2}<x ≤ 7$。
因为不等式组至少有$3$个整数解,即$5$,$6$,$7$,
所以$\frac{5 + m}{2}<5$,
解得$m<5$。
$m<5$
10. 如图,在$ △ A B C $中,$ ∠ C A B = n^{\circ}, ∠ C B A = m^{\circ}, D $是$ △ A B C $三个内角平分线的交点,延长$ D B $到点$ G, ∠ F C B $与$ ∠ C B G $的平分线交于点$ E $.若$ B E // A C $,则$ \frac{4}{5} n + \frac{3}{5} m = $
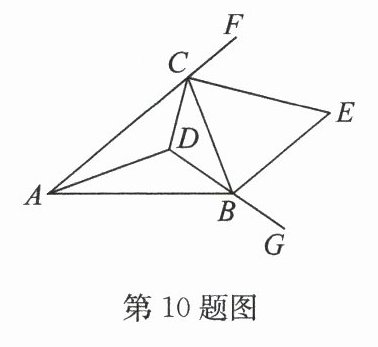
$ 72^{\circ} $
.
答案:10. $ 72^{\circ} $
解析:
证明:
∵D是△ABC内角平分线交点,
∴∠ABD=∠CBD=$\frac{m^{\circ}}{2}$,∠BAD=∠CAD=$\frac{n^{\circ}}{2}$,∠ACD=∠BCD=$\frac{180^{\circ}-n^{\circ}-m^{\circ}}{2}$=90°-$\frac{n^{\circ}+m^{\circ}}{2}$.
∵∠CBG是∠CBA的邻补角,
∴∠CBG=180°-m°,
∵BE平分∠CBG,
∴∠CBE=$\frac{1}{2}$∠CBG=90°-$\frac{m^{\circ}}{2}$.
∵BE//AC,
∴∠ACB=∠CBE(两直线平行,内错角相等),
即180°-n°-m°=90°-$\frac{m^{\circ}}{2}$,
化简得:n°+$\frac{m^{\circ}}{2}$=90°,
两边同乘$\frac{4}{5}$:$\frac{4}{5}n^{\circ}$+$\frac{2}{5}m^{\circ}$=72°,
两边加$\frac{1}{5}m^{\circ}$:$\frac{4}{5}n^{\circ}$+$\frac{3}{5}m^{\circ}$=72°+$\frac{1}{5}m^{\circ}$.
又
∵∠FCB+∠ACB=180°,CE平分∠FCB,
∠ECB=$\frac{1}{2}$(180°-∠ACB)=90°-$\frac{1}{2}$∠ACB,
∠E=180°-∠ECB-∠CBE=180°-[90°-$\frac{1}{2}$∠ACB]-[90°-$\frac{m^{\circ}}{2}$]=$\frac{1}{2}$∠ACB+$\frac{m^{\circ}}{2}$,
由∠ACB=180°-n°-m°,代入得∠E=90°-$\frac{n^{\circ}}{2}$,
结合BE//AC得∠E=∠ACF=∠FCB=180°-∠ACB,
即90°-$\frac{n^{\circ}}{2}$=180°-(180°-n°-m°),
化简得:90°-$\frac{n^{\circ}}{2}$=n°+m°,
联立n°+$\frac{m^{\circ}}{2}$=90°,解得n°=36°,m°=108°,
∴$\frac{4}{5}n^{\circ}$+$\frac{3}{5}m^{\circ}$=$\frac{4}{5}$×36°+$\frac{3}{5}$×108°=72°.
72°
∵D是△ABC内角平分线交点,
∴∠ABD=∠CBD=$\frac{m^{\circ}}{2}$,∠BAD=∠CAD=$\frac{n^{\circ}}{2}$,∠ACD=∠BCD=$\frac{180^{\circ}-n^{\circ}-m^{\circ}}{2}$=90°-$\frac{n^{\circ}+m^{\circ}}{2}$.
∵∠CBG是∠CBA的邻补角,
∴∠CBG=180°-m°,
∵BE平分∠CBG,
∴∠CBE=$\frac{1}{2}$∠CBG=90°-$\frac{m^{\circ}}{2}$.
∵BE//AC,
∴∠ACB=∠CBE(两直线平行,内错角相等),
即180°-n°-m°=90°-$\frac{m^{\circ}}{2}$,
化简得:n°+$\frac{m^{\circ}}{2}$=90°,
两边同乘$\frac{4}{5}$:$\frac{4}{5}n^{\circ}$+$\frac{2}{5}m^{\circ}$=72°,
两边加$\frac{1}{5}m^{\circ}$:$\frac{4}{5}n^{\circ}$+$\frac{3}{5}m^{\circ}$=72°+$\frac{1}{5}m^{\circ}$.
又
∵∠FCB+∠ACB=180°,CE平分∠FCB,
∠ECB=$\frac{1}{2}$(180°-∠ACB)=90°-$\frac{1}{2}$∠ACB,
∠E=180°-∠ECB-∠CBE=180°-[90°-$\frac{1}{2}$∠ACB]-[90°-$\frac{m^{\circ}}{2}$]=$\frac{1}{2}$∠ACB+$\frac{m^{\circ}}{2}$,
由∠ACB=180°-n°-m°,代入得∠E=90°-$\frac{n^{\circ}}{2}$,
结合BE//AC得∠E=∠ACF=∠FCB=180°-∠ACB,
即90°-$\frac{n^{\circ}}{2}$=180°-(180°-n°-m°),
化简得:90°-$\frac{n^{\circ}}{2}$=n°+m°,
联立n°+$\frac{m^{\circ}}{2}$=90°,解得n°=36°,m°=108°,
∴$\frac{4}{5}n^{\circ}$+$\frac{3}{5}m^{\circ}$=$\frac{4}{5}$×36°+$\frac{3}{5}$×108°=72°.
72°