11. (12分)(2024·宿城区期中)计算:(1)$ (π - 3.14)^{0}-(\frac{1}{2})^{-2}+|-2| $;
(2)$ 99^{2}-100 × 98 $;
(3)$ (-3 x y)^{2} · (-2 x^{2} y^{3})^{3} ÷ (-x y^{2}) $.
(2)$ 99^{2}-100 × 98 $;
(3)$ (-3 x y)^{2} · (-2 x^{2} y^{3})^{3} ÷ (-x y^{2}) $.
答案:11. 解: (1) 原式 $ = 1 - 4 + 2 = -3 + 2 = -1 $.
(2) 原式 $ = 99^{2} - (99 + 1) × (99 - 1) = 99^{2} - (99^{2} - 1) = 99^{2} - 99^{2} + 1 = 1 $.
(3) 原式 $ = 9x^{2}y^{2} · (-8x^{6}y^{9}) ÷ (-xy^{2}) = -72x^{8}y^{11} ÷ (-xy^{2}) = 72x^{7}y^{9} $.
(2) 原式 $ = 99^{2} - (99 + 1) × (99 - 1) = 99^{2} - (99^{2} - 1) = 99^{2} - 99^{2} + 1 = 1 $.
(3) 原式 $ = 9x^{2}y^{2} · (-8x^{6}y^{9}) ÷ (-xy^{2}) = -72x^{8}y^{11} ÷ (-xy^{2}) = 72x^{7}y^{9} $.
12. (12分)已知$ A = x^{2}-6 x + 10 $.
(1)当$ x $的值分别为$-2,0,3$时,求$ A $的值;
(2)证明:无论$ x $取什么值,$ A $的值都不小于1.
(1)当$ x $的值分别为$-2,0,3$时,求$ A $的值;
(2)证明:无论$ x $取什么值,$ A $的值都不小于1.
答案:12. (1) 解: 当 $ x = -2 $ 时, $ A = x^{2} - 6x + 10 = (-2)^{2} - 6 × (-2) + 10 = 4 + 12 + 10 = 26 $.
当 $ x = 0 $ 时, $ A = x^{2} - 6x + 10 = 0^{2} - 6 × 0 + 10 = 10 $.
当 $ x = 3 $ 时, $ A = x^{2} - 6x + 10 = 3^{2} - 6 × 3 + 10 = 9 - 18 + 10 = 1 $.
(2) 证明: $ A = x^{2} - 6x + 10 = x^{2} - 6x + 9 + 1 = (x - 3)^{2} + 1 $,
又因为无论 $ x $ 取什么值, 都有 $ (x - 3)^{2} ≥ 0 $, 从而 $ (x - 3)^{2} + 1 ≥ 1 $,
所以无论 $ x $ 取什么值, $ A $ 的值都不小于 1.
当 $ x = 0 $ 时, $ A = x^{2} - 6x + 10 = 0^{2} - 6 × 0 + 10 = 10 $.
当 $ x = 3 $ 时, $ A = x^{2} - 6x + 10 = 3^{2} - 6 × 3 + 10 = 9 - 18 + 10 = 1 $.
(2) 证明: $ A = x^{2} - 6x + 10 = x^{2} - 6x + 9 + 1 = (x - 3)^{2} + 1 $,
又因为无论 $ x $ 取什么值, 都有 $ (x - 3)^{2} ≥ 0 $, 从而 $ (x - 3)^{2} + 1 ≥ 1 $,
所以无论 $ x $ 取什么值, $ A $ 的值都不小于 1.
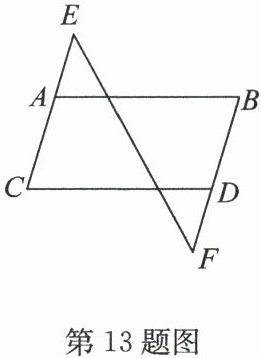
13. (12分)(2024·相城区期末)如图,现有以下3个论断:①$ A B // C D $;②$ ∠ B = ∠ C $;③$ ∠ E = ∠ F $.请以其中2个论断为条件,另一个论断为结论构造命题.
(1)请写出所有的真命题;
(2)请选择其中一个命题加以证明.
(1)请写出所有的真命题;
(2)请选择其中一个命题加以证明.

答案:13. 解: (1) 命题 1: 由①②得到③. 命题 2: 由①③得到②.
命题 3: 由②③得到①.
(2) 命题 1 证明如下:
因为 $ AB // CD $, 所以 $ ∠ B = ∠ CDF $.
又因为 $ ∠ B = ∠ C $, 所以 $ ∠ C = ∠ CDF $,
所以 $ AC // BD $, 所以 $ ∠ E = ∠ F $.
命题 2 证明如下:
因为 $ AB // CD $, 所以 $ ∠ B = ∠ CDF $.
因为 $ ∠ E = ∠ F $, 所以 $ CE // BF $,
所以 $ ∠ C = ∠ CDF $, 所以 $ ∠ B = ∠ C $.
命题 3 证明如下:
因为 $ ∠ E = ∠ F $, 所以 $ CE // BF $, 所以 $ ∠ C = ∠ CDF $.
又因为 $ ∠ B = ∠ C $, 所以 $ ∠ B = ∠ CDF $, 所以 $ AB // CD $.
命题 3: 由②③得到①.
(2) 命题 1 证明如下:
因为 $ AB // CD $, 所以 $ ∠ B = ∠ CDF $.
又因为 $ ∠ B = ∠ C $, 所以 $ ∠ C = ∠ CDF $,
所以 $ AC // BD $, 所以 $ ∠ E = ∠ F $.
命题 2 证明如下:
因为 $ AB // CD $, 所以 $ ∠ B = ∠ CDF $.
因为 $ ∠ E = ∠ F $, 所以 $ CE // BF $,
所以 $ ∠ C = ∠ CDF $, 所以 $ ∠ B = ∠ C $.
命题 3 证明如下:
因为 $ ∠ E = ∠ F $, 所以 $ CE // BF $, 所以 $ ∠ C = ∠ CDF $.
又因为 $ ∠ B = ∠ C $, 所以 $ ∠ B = ∠ CDF $, 所以 $ AB // CD $.
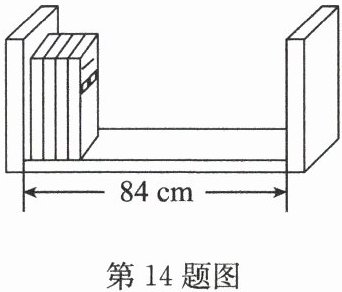
14. (14分)如图,书架宽84cm,在该书架上按图示方式摆放数学书和语文书,已知每本数学书厚0.8cm,每本语文书厚1.2cm.
(1)数学书和语文书共90本恰好摆满该书架,求书架上数学书和语文书各有多少本;
(2)如果书架上已摆放了10本语文书,那么数学书最多还可以摆放多少本?
(1)数学书和语文书共90本恰好摆满该书架,求书架上数学书和语文书各有多少本;
(2)如果书架上已摆放了10本语文书,那么数学书最多还可以摆放多少本?

答案:14. 解: (1) 设书架上数学书有 $ x $ 本, 则语文书有 $ (90 - x) $ 本.
根据题意, 得 $ 0.8x + 1.2(90 - x) = 84 $, 解得 $ x = 60 $,
所以 $ 90 - x = 30 $.
答: 书架上数学书有 60 本, 语文书有 30 本.
(2) 设数学书还可以摆放 $ m $ 本, 则 $ 10 × 1.2 + 0.8m ≤ 84 $, 解得 $ m ≤ 90 $.
答: 数学书最多还可以摆放 90 本.
根据题意, 得 $ 0.8x + 1.2(90 - x) = 84 $, 解得 $ x = 60 $,
所以 $ 90 - x = 30 $.
答: 书架上数学书有 60 本, 语文书有 30 本.
(2) 设数学书还可以摆放 $ m $ 本, 则 $ 10 × 1.2 + 0.8m ≤ 84 $, 解得 $ m ≤ 90 $.
答: 数学书最多还可以摆放 90 本.