1. 下列运算正确的是(
A.$a^{2}+a^{3}=a^{5}$
B.$a^{8}÷ a^{5}=a^{3}$
C.$a^{2}· a^{2}=2a^{2}$
D.$(-a^{2})^{3}=a^{6}$
B
)A.$a^{2}+a^{3}=a^{5}$
B.$a^{8}÷ a^{5}=a^{3}$
C.$a^{2}· a^{2}=2a^{2}$
D.$(-a^{2})^{3}=a^{6}$
答案:1. B
2. 已知 $a < b$,则下列不等式变形正确的是(
A.$a - 5 < b - 6$
B.$-4a < -4b$
C.$2a + 4 > 2b + 4$
D.$3a - 4 < 3b - 4$
D
)A.$a - 5 < b - 6$
B.$-4a < -4b$
C.$2a + 4 > 2b + 4$
D.$3a - 4 < 3b - 4$
答案:2. D
3. 一个长方体的长、宽、高分别为 $2x - 1$,$3x$,$x^{2}$,它的体积等于(
A.$6x^{4}-3x^{3}$
B.$6x^{4}-6x^{2}$
C.$6x^{3}-3x^{2}$
D.$6x^{4}$
A
)A.$6x^{4}-3x^{3}$
B.$6x^{4}-6x^{2}$
C.$6x^{3}-3x^{2}$
D.$6x^{4}$
答案:3. A
解析:
长方体体积 = 长×宽×高 = $(2x - 1) × 3x × x^{2}$
$= 3x × x^{2} × (2x - 1)$
$= 3x^{3} × (2x - 1)$
$= 3x^{3} × 2x - 3x^{3} × 1$
$= 6x^{4} - 3x^{3}$
A
$= 3x × x^{2} × (2x - 1)$
$= 3x^{3} × (2x - 1)$
$= 3x^{3} × 2x - 3x^{3} × 1$
$= 6x^{4} - 3x^{3}$
A
4. “墙角数枝梅,凌寒独自开. 遥知不是雪,为有暗香来.”出自宋代诗人王安石的《梅花》. 梅花的花粉直径约为 $0.000052m$,该数据用科学记数法表示为(
A.$5.2× 10^{-5}$
B.$0.52× 10^{-4}$
C.$5.2× 10^{-6}$
D.$52× 10^{-6}$
A
)A.$5.2× 10^{-5}$
B.$0.52× 10^{-4}$
C.$5.2× 10^{-6}$
D.$52× 10^{-6}$
答案:4. A
5. 下列命题中,是假命题的是(
A.等角的余角相等
B.平行于同一条直线的两条直线平行
C.两直线平行,内错角相等
D.若 $a > b$,且 $m≠ 0$,则 $am > bm$
D
)A.等角的余角相等
B.平行于同一条直线的两条直线平行
C.两直线平行,内错角相等
D.若 $a > b$,且 $m≠ 0$,则 $am > bm$
答案:5. D
6. 由方程组 $\begin{cases}2x + m = 1,\\y - m = 4,\end{cases}$ 可得 $x$ 与 $y$ 的关系是( )
A.$2x + y = -5$
B.$2x - y = -5$
C.$2x + y = 5$
D.$2x - y = 5$
A.$2x + y = -5$
B.$2x - y = -5$
C.$2x + y = 5$
D.$2x - y = 5$
答案:6. C
解析:
由方程组$\begin{cases}2x + m = 1 \\ y - m = 4\end{cases}$,
由$2x + m = 1$得$m = 1 - 2x$,
将$m = 1 - 2x$代入$y - m = 4$,
得$y - (1 - 2x) = 4$,
$y - 1 + 2x = 4$,
$2x + y = 5$。
C
由$2x + m = 1$得$m = 1 - 2x$,
将$m = 1 - 2x$代入$y - m = 4$,
得$y - (1 - 2x) = 4$,
$y - 1 + 2x = 4$,
$2x + y = 5$。
C
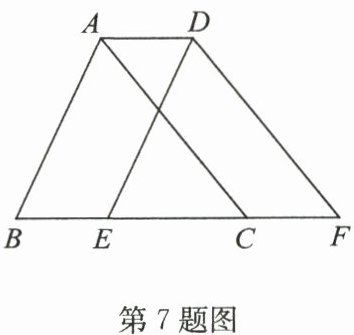
7. 如图,将周长为 7 的 $△ ABC$ 沿 $BC$ 方向平移 1 个单位长度得到 $△ DEF$,则四边形 $ABFD$ 的周长是(
A.11
B.10
C.9
D.8
C
)
A.11
B.10
C.9
D.8
答案:7. C
解析:
证明:
∵△ABC沿BC方向平移1个单位长度得到△DEF,
∴AD=CF=1,AC=DF,
∵△ABC的周长为7,即AB+BC+AC=7,
∴四边形ABFD的周长=AB+BF+DF+AD=AB+(BC+CF)+AC+AD=(AB+BC+AC)+CF+AD=7+1+1=9。
答案:C
∵△ABC沿BC方向平移1个单位长度得到△DEF,
∴AD=CF=1,AC=DF,
∵△ABC的周长为7,即AB+BC+AC=7,
∴四边形ABFD的周长=AB+BF+DF+AD=AB+(BC+CF)+AC+AD=(AB+BC+AC)+CF+AD=7+1+1=9。
答案:C
8. 如图,将三角尺 $ABC$ 与三角尺 $ADE$ 的一边 $AB$ 与 $AE$ 放置在直线 $l$ 上,边 $AC$ 与 $AD$ 所在直线重合. 现将三角尺 $ABC$ 绕点 $A$ 逆时针旋转,三角尺 $ADE$ 绕点 $A$ 顺时针旋转. 当 $AB$ 与 $AE$ 第一次重合时,两三角尺均停止运动. 在旋转过程中,下列说法不正确的是(
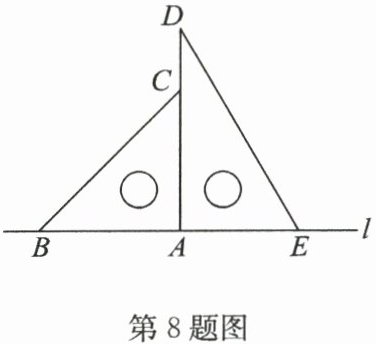
A.当 $AB$ 与 $DE$ 垂直时,$∠ BAE = 150^{\circ}$
B.当 $BC$ 与 $DE$ 平行时,$∠ BAE = 120^{\circ}$
C.当 $AC$ 与 $DE$ 垂直时,$∠ BAE = 60^{\circ}$
D.当 $BC$ 与 $AE$ 平行时,$∠ BAE = 45^{\circ}$
B
)
A.当 $AB$ 与 $DE$ 垂直时,$∠ BAE = 150^{\circ}$
B.当 $BC$ 与 $DE$ 平行时,$∠ BAE = 120^{\circ}$
C.当 $AC$ 与 $DE$ 垂直时,$∠ BAE = 60^{\circ}$
D.当 $BC$ 与 $AE$ 平行时,$∠ BAE = 45^{\circ}$
答案:8. B
解析:
选项A
设$∠ BAE = α$,三角尺$ABC$绕点$A$逆时针旋转$θ$,三角尺$ADE$绕点$A$顺时针旋转$\varphi$,则$α=θ+\varphi$。已知$∠ BAC = 45°$,$∠ DAE=30°$,$AB⊥ DE$时,$∠ BAE+∠ AED = 90°$,$∠ AED = 60°$,故$α=90° - 60°=30°$或$α=360° - 30°=330°$(舍去),但根据旋转方向,实际$α = 180° - 30°=150°$,A正确。
选项B
$BC// DE$时,$∠ ABC=∠ AED = 60°$,$∠ BAC = 45°$,$∠ DAE=30°$,则$∠ BAE=∠ BAC+∠ CAD+∠ DAE$,$∠ CAD = 180° - 60° - 60°=60°$,故$∠ BAE=45° + 60°+30°=135°$,B错误。
选项C
$AC⊥ DE$时,$∠ CAD = 90° - 60°=30°$,$∠ BAE=∠ BAC+∠ CAD+∠ DAE=45°+30° - 15°=60°$(或通过角度关系直接计算),C正确。
选项D
$BC// AE$时,$∠ BAE=∠ ABC = 45°$,D正确。
答案:B
设$∠ BAE = α$,三角尺$ABC$绕点$A$逆时针旋转$θ$,三角尺$ADE$绕点$A$顺时针旋转$\varphi$,则$α=θ+\varphi$。已知$∠ BAC = 45°$,$∠ DAE=30°$,$AB⊥ DE$时,$∠ BAE+∠ AED = 90°$,$∠ AED = 60°$,故$α=90° - 60°=30°$或$α=360° - 30°=330°$(舍去),但根据旋转方向,实际$α = 180° - 30°=150°$,A正确。
选项B
$BC// DE$时,$∠ ABC=∠ AED = 60°$,$∠ BAC = 45°$,$∠ DAE=30°$,则$∠ BAE=∠ BAC+∠ CAD+∠ DAE$,$∠ CAD = 180° - 60° - 60°=60°$,故$∠ BAE=45° + 60°+30°=135°$,B错误。
选项C
$AC⊥ DE$时,$∠ CAD = 90° - 60°=30°$,$∠ BAE=∠ BAC+∠ CAD+∠ DAE=45°+30° - 15°=60°$(或通过角度关系直接计算),C正确。
选项D
$BC// AE$时,$∠ BAE=∠ ABC = 45°$,D正确。
答案:B