9. 不等式 $6 - x > 0$ 的解集是
$ x < 6 $
.答案:9. $ x < 6 $
解析:
$x < 6$
10. 计算:$-2a^{2}b^{3}· 3a=$
$ -6a^{3}b^{3} $
.答案:10. $ -6a^{3}b^{3} $
11. 若 $a^{2}-b^{2}=56$,$a - b = 7$,则 $a + b=$
8
.答案:11. 8
解析:
因为$a^{2}-b^{2}=(a - b)(a + b)$,已知$a^{2}-b^{2}=56$,$a - b = 7$,所以$7(a + b)=56$,则$a + b=56÷7=8$。
12. 如图,$△ A'B'C'$ 由 $△ ABC$ 绕点 $O$ 旋转 $180^{\circ}$ 而得到,有下列结论:①点 $A$ 与点 $A'$ 是对应点;② $BO = B'O$;③ $∠ ACB = ∠ C'A'B'$;④ $AB = A'B'$. 其中成立的是
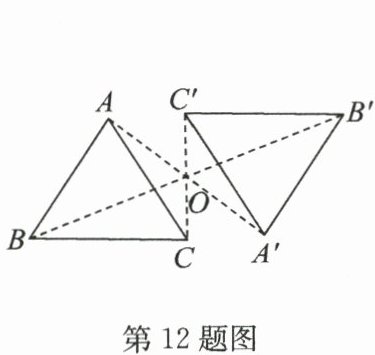
①②④
.(填序号)
答案:12. ①②④
13. 命题“如果一个三角形的两个角互余,那么这个三角形是直角三角形”的逆命题是
直角三角形的两锐角互余
.答案:13. 直角三角形的两锐角互余
14. 如图,将直角 $△ ABC$ 沿 $AB$ 方向平移 $2cm$ 得到 $△ DEF$,$DF$ 交 $BC$ 于点 $H$,$CH = 2cm$,$EF = 5cm$,则阴影部分的面积为
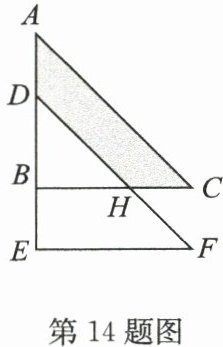
$ 8cm^{2} $
.
答案:14. $ 8cm^{2} $
解析:
解:由平移性质得:$BC=EF=5\,\mathrm{cm}$,$AD=BE=2\,\mathrm{cm}$,$△ ABC ≌ △ DEF$,
$\therefore BH=BC-CH=5-2=3\,\mathrm{cm}$,
$\because S_{\mathrm{阴影}}=S_{△ ABC}-S_{△ DBH}$,$S_{△ DEF}=S_{△ ABC}$,
$\therefore S_{\mathrm{阴影}}=S_{\mathrm{梯形}BEFH}$,
$\because$ 平移得 $EF // BC$,$BE ⊥ EF$,
$\therefore S_{\mathrm{梯形}BEFH}=\frac{1}{2}(BH+EF)· BE=\frac{1}{2}×(3+5)×2=8\,\mathrm{cm}^2$,
即阴影部分面积为$8\,\mathrm{cm}^2$。
$\therefore BH=BC-CH=5-2=3\,\mathrm{cm}$,
$\because S_{\mathrm{阴影}}=S_{△ ABC}-S_{△ DBH}$,$S_{△ DEF}=S_{△ ABC}$,
$\therefore S_{\mathrm{阴影}}=S_{\mathrm{梯形}BEFH}$,
$\because$ 平移得 $EF // BC$,$BE ⊥ EF$,
$\therefore S_{\mathrm{梯形}BEFH}=\frac{1}{2}(BH+EF)· BE=\frac{1}{2}×(3+5)×2=8\,\mathrm{cm}^2$,
即阴影部分面积为$8\,\mathrm{cm}^2$。
15. 已知 $\begin{cases}x = 3,\\y = -2\end{cases}$ 是关于 $x$,$y$ 的方程 $6x + my = 30$ 的解,则 $m=$ ______ .
答案:15. -6
解析:
将$x = 3$,$y = -2$代入方程$6x + my = 30$,得$6×3 + m×(-2) = 30$,即$18 - 2m = 30$,移项得$-2m = 30 - 18$,$-2m = 12$,解得$m = -6$。
$-6$
$-6$
16. 已知 $x$,$y$ 满足方程组 $\begin{cases}3x + y = 2025,\\x + 3y = 2026,\end{cases}$ 则 $x - y=$ ______ .
答案:16. $ -\frac{1}{2} $
解析:
$\begin{cases}3x + y = 2025,\\x + 3y = 2026,\end{cases}$
用第一个方程减去第二个方程:$(3x + y) - (x + 3y) = 2025 - 2026$
$3x + y - x - 3y = -1$
$2x - 2y = -1$
$2(x - y) = -1$
$x - y = -\frac{1}{2}$
$-\frac{1}{2}$
用第一个方程减去第二个方程:$(3x + y) - (x + 3y) = 2025 - 2026$
$3x + y - x - 3y = -1$
$2x - 2y = -1$
$2(x - y) = -1$
$x - y = -\frac{1}{2}$
$-\frac{1}{2}$
17. 某次测试共有 20 道题,每答对一道题得 5 分,每答错一道题扣 1 分. 若小明得分要超过 80 分,则小明至少要答对
17
道题.答案:17. 17
解析:
设小明答对$x$道题,则答错$(20 - x)$道题。
根据题意,得$5x - 1×(20 - x) > 80$
$5x - 20 + x > 80$
$6x > 100$
$x > \frac{100}{6}$
$x > 16\frac{2}{3}$
因为$x$为整数,所以$x$的最小值为$17$。
17
根据题意,得$5x - 1×(20 - x) > 80$
$5x - 20 + x > 80$
$6x > 100$
$x > \frac{100}{6}$
$x > 16\frac{2}{3}$
因为$x$为整数,所以$x$的最小值为$17$。
17
18. 如果 $x$ 是一个有理数,我们定义 $\{x\}$ 表示不小于 $x$ 的最小整数,如 $\{3.4\} = 4$,$\{-2.8\} = -2$. 若 $\{2a + 6\} = 4$,则 $a$ 的取值范围是
$ -\frac{3}{2} < a ≤ -1 $
.答案:18. $ -\frac{3}{2} < a ≤ -1 $
解析:
因为$\{x\}$表示不小于$x$的最小整数,且$\{2a + 6\} = 4$,所以$3 < 2a + 6 ≤ 4$。
解不等式$3 < 2a + 6$,得$3 - 6 < 2a$,即$-3 < 2a$,所以$a > -\frac{3}{2}$。
解不等式$2a + 6 ≤ 4$,得$2a ≤ 4 - 6$,即$2a ≤ -2$,所以$a ≤ -1$。
综上,$a$的取值范围是$-\frac{3}{2} < a ≤ -1$。
解不等式$3 < 2a + 6$,得$3 - 6 < 2a$,即$-3 < 2a$,所以$a > -\frac{3}{2}$。
解不等式$2a + 6 ≤ 4$,得$2a ≤ 4 - 6$,即$2a ≤ -2$,所以$a ≤ -1$。
综上,$a$的取值范围是$-\frac{3}{2} < a ≤ -1$。
19. (10 分)(1)计算:$-3^{2}+2026^{0}-(-\frac{1}{2})^{-1}$; (2)化简:$3(m + n)^{2}-2(m + n)(m - n)$.
答案:19. 解: (1) 原式 $ = -9 + 1 - (-2) = -9 + 1 + 2 = -6 $.
(2) 原式 $ = 3(m^{2} + 2mn + n^{2}) - 2(m^{2} - n^{2}) = 3m^{2} + 6mn + 3n^{2} - 2m^{2} + 2n^{2} = m^{2} + 6mn + 5n^{2} $.
(2) 原式 $ = 3(m^{2} + 2mn + n^{2}) - 2(m^{2} - n^{2}) = 3m^{2} + 6mn + 3n^{2} - 2m^{2} + 2n^{2} = m^{2} + 6mn + 5n^{2} $.
20. (10 分)解方程组:
(1) $\begin{cases}2x - y = 3,\\3x - 2y = 4;\end{cases}$
(2) $\begin{cases}4x - 3y = 15,\\2x + 5y = 1.\end{cases}$
(1) $\begin{cases}2x - y = 3,\\3x - 2y = 4;\end{cases}$
(2) $\begin{cases}4x - 3y = 15,\\2x + 5y = 1.\end{cases}$
答案:20. 解: (1) $ \begin{cases} 2x - y = 3, ① \\ 3x - 2y = 4, ② \end{cases} $
①×2 - ②, 得 $ x = 2 $.
把 $ x = 2 $ 代入①, 得 $ 4 - y = 3 $, 解得 $ y = 1 $.
所以原方程组的解为 $ \begin{cases} x = 2, \\ y = 1. \end{cases} $
(2) $ \begin{cases} 4x - 3y = 15, ① \\ 2x + 5y = 1, ② \end{cases} $
②×2 - ①, 得 $ 13y = -13, y = -1 $.
把 $ y = -1 $ 代入②, 得 $ 2x - 5 = 1 $, 解得 $ x = 3 $.
所以原方程组的解为 $ \begin{cases} x = 3, \\ y = -1. \end{cases} $
①×2 - ②, 得 $ x = 2 $.
把 $ x = 2 $ 代入①, 得 $ 4 - y = 3 $, 解得 $ y = 1 $.
所以原方程组的解为 $ \begin{cases} x = 2, \\ y = 1. \end{cases} $
(2) $ \begin{cases} 4x - 3y = 15, ① \\ 2x + 5y = 1, ② \end{cases} $
②×2 - ①, 得 $ 13y = -13, y = -1 $.
把 $ y = -1 $ 代入②, 得 $ 2x - 5 = 1 $, 解得 $ x = 3 $.
所以原方程组的解为 $ \begin{cases} x = 3, \\ y = -1. \end{cases} $
21. (8 分)填空:
已知:如图,$AC$,$BD$ 相交于点 $O$.
求证:$∠ A + ∠ B = ∠ C + ∠ D$.
证明:$\because ∠ A + ∠ B + ∠ 1 = 180^{\circ}$(
$\therefore ∠ A + ∠ B = 180^{\circ}-∠$
同理可得 $∠ C + ∠ D = 180^{\circ}-∠$
又 $\because ∠ 1 = ∠ 2$(
$\therefore ∠ A + ∠ B = ∠ C + ∠ D$(等量代换).
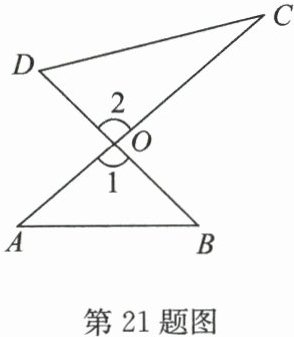
已知:如图,$AC$,$BD$ 相交于点 $O$.
求证:$∠ A + ∠ B = ∠ C + ∠ D$.
证明:$\because ∠ A + ∠ B + ∠ 1 = 180^{\circ}$(
三角形内角和等于 $ 180^{\circ} $
),$\therefore ∠ A + ∠ B = 180^{\circ}-∠$
1
(等式的性质).同理可得 $∠ C + ∠ D = 180^{\circ}-∠$
2
.又 $\because ∠ 1 = ∠ 2$(
对顶角相等
),$\therefore ∠ A + ∠ B = ∠ C + ∠ D$(等量代换).

答案:21. 三角形内角和等于 $ 180^{\circ} $ 1 2 对顶角相等
解析:
证明:$\because ∠ A + ∠ B + ∠ 1 = 180^{\circ}$(三角形内角和等于$180^{\circ}$),
$\therefore ∠ A + ∠ B = 180^{\circ}-∠ 1$(等式的性质).
同理可得 $∠ C + ∠ D = 180^{\circ}-∠ 2$.
又 $\because ∠ 1 = ∠ 2$(对顶角相等),
$\therefore ∠ A + ∠ B = ∠ C + ∠ D$(等量代换).
$\therefore ∠ A + ∠ B = 180^{\circ}-∠ 1$(等式的性质).
同理可得 $∠ C + ∠ D = 180^{\circ}-∠ 2$.
又 $\because ∠ 1 = ∠ 2$(对顶角相等),
$\therefore ∠ A + ∠ B = ∠ C + ∠ D$(等量代换).