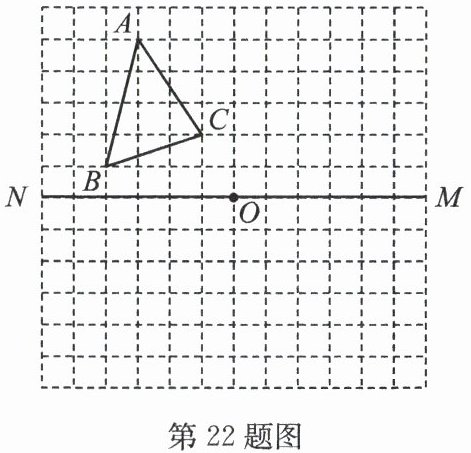
22. (10 分)在如图所示的方格纸中,$△ ABC$ 的顶点都在边长为 1 个单位长度的小正方形的顶点上. 按下列要求画图与填空:
(1)将 $△ ABC$ 向上平移 1 个单位长度,再向右平移 5 个单位长度,画出得到的图形 $△ A_{1}B_{1}C_{1}$;
(2)画出 $△ ABC$ 关于直线 $MN$ 对称的 $△ A_{2}B_{2}C_{2}$;
(3)画出 $△ ABC$ 绕点 $O$ 旋转 $180^{\circ}$ 后的图形 $△ A_{3}B_{3}C_{3}$;
(4)连接 $AA_{1}$,$BB_{1}$,则 $AA_{1}$ 与 $BB_{1}$ 的关系是
(1)将 $△ ABC$ 向上平移 1 个单位长度,再向右平移 5 个单位长度,画出得到的图形 $△ A_{1}B_{1}C_{1}$;
(2)画出 $△ ABC$ 关于直线 $MN$ 对称的 $△ A_{2}B_{2}C_{2}$;
(3)画出 $△ ABC$ 绕点 $O$ 旋转 $180^{\circ}$ 后的图形 $△ A_{3}B_{3}C_{3}$;
(4)连接 $AA_{1}$,$BB_{1}$,则 $AA_{1}$ 与 $BB_{1}$ 的关系是
平行且相等
.
答案:
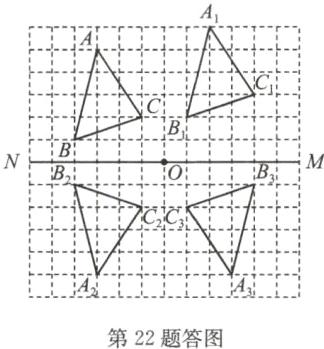
22. 解: (1)(2)(3) 如答图所示.
(4) 平行且相等
22. 解: (1)(2)(3) 如答图所示.
(4) 平行且相等

23. (10 分)解下列不等式(组):
(1) $1-\frac{x + 6}{2}<\frac{2x + 1}{3}$;
(2) $\begin{cases}x - 1 < 0,\frac{5x + 1}{2}≥ x - 1.\end{cases}$
(1) $1-\frac{x + 6}{2}<\frac{2x + 1}{3}$;
(2) $\begin{cases}x - 1 < 0,\frac{5x + 1}{2}≥ x - 1.\end{cases}$
答案:23. 解: (1) 去分母, 得 $ 6 - 3(x + 6) < 2(2x + 1) $,
去括号, 得 $ 6 - 3x - 18 < 4x + 2 $,
移项, 得 $ -3x - 4x < 2 - 6 + 18 $,
合并同类项, 得 $ -7x < 14 $,
两边都除以 -7, 得 $ x > -2 $.
(2) $ \begin{cases} x - 1 < 0, ① \\ \frac{5x + 1}{2} ≥ x - 1, ② \end{cases} $
解不等式①, 得 $ x < 1 $,
解不等式②, 得 $ x ≥ -1 $,
所以原不等式组的解集为 $ -1 ≤ x < 1 $.
去括号, 得 $ 6 - 3x - 18 < 4x + 2 $,
移项, 得 $ -3x - 4x < 2 - 6 + 18 $,
合并同类项, 得 $ -7x < 14 $,
两边都除以 -7, 得 $ x > -2 $.
(2) $ \begin{cases} x - 1 < 0, ① \\ \frac{5x + 1}{2} ≥ x - 1, ② \end{cases} $
解不等式①, 得 $ x < 1 $,
解不等式②, 得 $ x ≥ -1 $,
所以原不等式组的解集为 $ -1 ≤ x < 1 $.
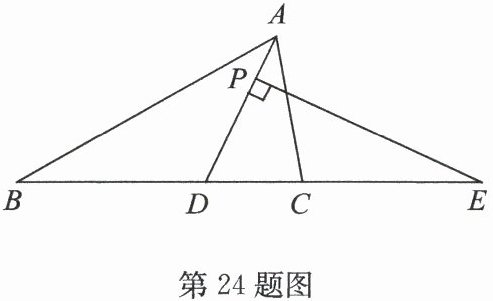
24. (10 分)如图,在 $△ ABC$ 中,$AD$ 平分 $∠ BAC$,$P$ 是线段 $AD$ 上的一个动点,$PE⊥ AD$ 交直线 $BC$ 于点 $E$.
(1)若 $∠ B = 30^{\circ}$,$∠ ACB = 80^{\circ}$,求 $∠ E$ 的度数;
(2)当点 $P$ 在线段 $AD$ 上运动时,若 $∠ E$ 是锐角,请直接写出 $∠ E$,$∠ ACB$,$∠ B$ 之间的关系.
(1)若 $∠ B = 30^{\circ}$,$∠ ACB = 80^{\circ}$,求 $∠ E$ 的度数;
(2)当点 $P$ 在线段 $AD$ 上运动时,若 $∠ E$ 是锐角,请直接写出 $∠ E$,$∠ ACB$,$∠ B$ 之间的关系.

答案:24. 解: (1) 因为 $ ∠ B = 30^{\circ}, ∠ ACB = 80^{\circ} $,
所以 $ ∠ BAC = 180^{\circ} - ∠ B - ∠ ACB = 70^{\circ} $.
因为 $ AD $ 平分 $ ∠ BAC $,
所以 $ ∠ BAD = \frac{1}{2} ∠ BAC = 35^{\circ} $,
所以 $ ∠ PDE = ∠ B + ∠ BAD = 65^{\circ} $.
因为 $ PE ⊥ AD $,
所以 $ ∠ E = 90^{\circ} - ∠ PDE = 25^{\circ} $.
(2) 因为 $ AD $ 平分 $ ∠ BAC $,
所以 $ ∠ BAD = \frac{1}{2} ∠ BAC = \frac{1}{2}(180^{\circ} - ∠ B - ∠ ACB) $,
所以 $ ∠ PDE = ∠ B + ∠ BAD = ∠ B + \frac{1}{2}(180^{\circ} - ∠ B - ∠ ACB) = 90^{\circ} + \frac{1}{2} ∠ B - \frac{1}{2} ∠ ACB $.
因为 $ PE ⊥ AD $, 所以 $ ∠ E = 90^{\circ} - ∠ PDE $
$ = 90^{\circ} - (90^{\circ} + \frac{1}{2} ∠ B - \frac{1}{2} ∠ ACB) $
$ = \frac{1}{2}(∠ ACB - ∠ B) $.
所以 $ ∠ BAC = 180^{\circ} - ∠ B - ∠ ACB = 70^{\circ} $.
因为 $ AD $ 平分 $ ∠ BAC $,
所以 $ ∠ BAD = \frac{1}{2} ∠ BAC = 35^{\circ} $,
所以 $ ∠ PDE = ∠ B + ∠ BAD = 65^{\circ} $.
因为 $ PE ⊥ AD $,
所以 $ ∠ E = 90^{\circ} - ∠ PDE = 25^{\circ} $.
(2) 因为 $ AD $ 平分 $ ∠ BAC $,
所以 $ ∠ BAD = \frac{1}{2} ∠ BAC = \frac{1}{2}(180^{\circ} - ∠ B - ∠ ACB) $,
所以 $ ∠ PDE = ∠ B + ∠ BAD = ∠ B + \frac{1}{2}(180^{\circ} - ∠ B - ∠ ACB) = 90^{\circ} + \frac{1}{2} ∠ B - \frac{1}{2} ∠ ACB $.
因为 $ PE ⊥ AD $, 所以 $ ∠ E = 90^{\circ} - ∠ PDE $
$ = 90^{\circ} - (90^{\circ} + \frac{1}{2} ∠ B - \frac{1}{2} ∠ ACB) $
$ = \frac{1}{2}(∠ ACB - ∠ B) $.
25. (12 分)已知二元一次方程 $5x + 3y = 18$.
(1)把方程写成用含 $x$ 的代数式表示 $y$ 的形式,即 $y=$
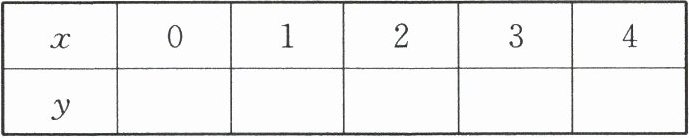
(2)填表,使 $x$,$y$ 的值是方程 $5x + 3y = 18$ 的解;
(3)根据表格,请直接写出方程 $5x + 3y = 18$ 的非负整数解.
(1)把方程写成用含 $x$ 的代数式表示 $y$ 的形式,即 $y=$
$ \frac{18 - 5x}{3} $
;(2)填表,使 $x$,$y$ 的值是方程 $5x + 3y = 18$ 的解;

(3)根据表格,请直接写出方程 $5x + 3y = 18$ 的非负整数解.
答案:25. (1) $ \frac{18 - 5x}{3} $
(2) $ 6 \frac{13}{3} \frac{8}{3} 1 -\frac{2}{3} $
(3) 解: 原方程 $ 5x + 3y = 18 $ 的非负整数解为 $ \begin{cases} x = 0, \\ y = 6, \end{cases} \begin{cases} x = 3, \\ y = 1. \end{cases} $
(2) $ 6 \frac{13}{3} \frac{8}{3} 1 -\frac{2}{3} $
(3) 解: 原方程 $ 5x + 3y = 18 $ 的非负整数解为 $ \begin{cases} x = 0, \\ y = 6, \end{cases} \begin{cases} x = 3, \\ y = 1. \end{cases} $