26. (12 分)【知识生成】通过第 8 章的学习,我们已经知道,对于一个图形,通过不同的方法计算它的面积可以得到一个数学等式,请结合图形解答下列问题:
(1) 写出图①中所表示的数学等式:
(2) 如图②,用 4 块完全相同的长方形拼成正方形,用两种不同的方法求图中阴影部分的面积,得到的数学等式是
(3) 【知识应用】若$x + y = 7$,$xy = \dfrac{13}{4}$,求$x - y$的值;
(4) 【灵活应用】图③中有两个正方形$A$,$B$,现将$B$放在$A$的内部得到图甲,将$A$,$B$并列放置后构造新的正方形得到图乙. 若图甲和图乙中阴影部分的面积分别为 2 和 11,则正方形$A$,$B$的面积之和为
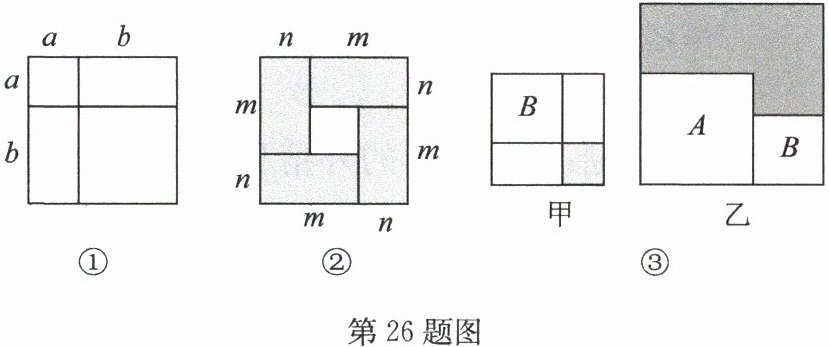
(1) 写出图①中所表示的数学等式:
$(a + b)^{2} = a^{2} + 2ab + b^{2}$
;(2) 如图②,用 4 块完全相同的长方形拼成正方形,用两种不同的方法求图中阴影部分的面积,得到的数学等式是
$(m + n)^{2} - (m - n)^{2} = 4mn$
;(3) 【知识应用】若$x + y = 7$,$xy = \dfrac{13}{4}$,求$x - y$的值;
(4) 【灵活应用】图③中有两个正方形$A$,$B$,现将$B$放在$A$的内部得到图甲,将$A$,$B$并列放置后构造新的正方形得到图乙. 若图甲和图乙中阴影部分的面积分别为 2 和 11,则正方形$A$,$B$的面积之和为
13
.
答案:26. (1) $ (a + b)^{2} = a^{2} + 2ab + b^{2} $
(2) $ (m + n)^{2} - (m - n)^{2} = 4mn $
(3) 解: 因为 $ x + y = 7 $, $ xy = \frac{13}{4} $,
所以 $ (x - y)^{2} = (x + y)^{2} - 4xy = 7^{2} - 4 × \frac{13}{4} = 49 - 13 = 36 $. 所以 $ x - y = ±6 $.
(4) 13
(2) $ (m + n)^{2} - (m - n)^{2} = 4mn $
(3) 解: 因为 $ x + y = 7 $, $ xy = \frac{13}{4} $,
所以 $ (x - y)^{2} = (x + y)^{2} - 4xy = 7^{2} - 4 × \frac{13}{4} = 49 - 13 = 36 $. 所以 $ x - y = ±6 $.
(4) 13
27. (12 分)在数学实践活动课上,小亮同学利用一副三角尺探索与研究共直角顶点的两个直角三角形中的位置关系与数量关系. (其中$∠ A = 30^{\circ}$,$∠ B = 60^{\circ}$,$∠ C = ∠ D = 45^{\circ}$)
(1) 将三角尺如图①所示叠放在一起.
①$∠ AOD$与$∠ BOC$的大小关系是
②$∠ BOD$与$∠ AOC$的数量关系是
(2) 小亮固定其中一块三角尺$△ COD$不变,绕点$O$顺时针转动另一块三角尺,从图②的$OA$与$OC$重合开始,到图③的$OA$与$OC$在一条直线上时结束,探索$△ AOB$的一边与$△ COD$的一边平行的情况.
①如图④,当$AB // CD$时,求$∠ AOC$的大小;
②直接写出$∠ AOC$的其余所有可能的度数.
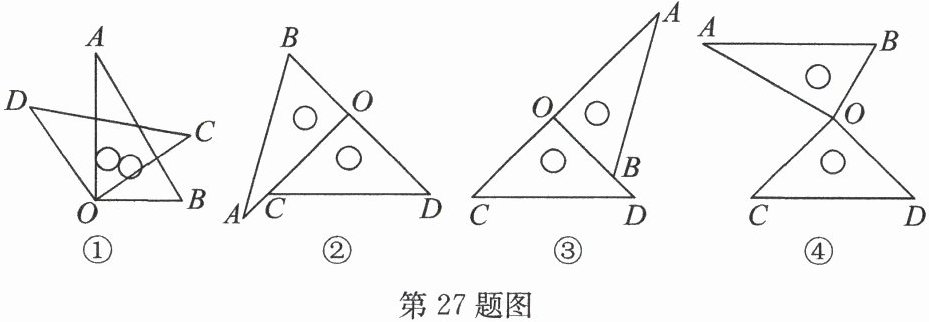
(1) 将三角尺如图①所示叠放在一起.
①$∠ AOD$与$∠ BOC$的大小关系是
相等
;②$∠ BOD$与$∠ AOC$的数量关系是
互补
.(2) 小亮固定其中一块三角尺$△ COD$不变,绕点$O$顺时针转动另一块三角尺,从图②的$OA$与$OC$重合开始,到图③的$OA$与$OC$在一条直线上时结束,探索$△ AOB$的一边与$△ COD$的一边平行的情况.
①如图④,当$AB // CD$时,求$∠ AOC$的大小;
②直接写出$∠ AOC$的其余所有可能的度数.

答案:
27. (1) ① 相等 ② 互补
(2) 解: ① 如答图①, 过点 $ O $ 作 $ OE // AB $,

又因为 $ AB // CD $, 所以 $ AB // CD // OE $,
所以 $ ∠AOE = ∠A = 30^{\circ} $, $ ∠COE = ∠C = 45^{\circ} $,
所以 $ ∠AOC = ∠AOE + ∠COE = 75^{\circ} $.
② 当 $ AB // OC $ 时, 如答图②, 则 $ ∠AOC = ∠A = 30^{\circ} $;
当 $ OA // CD $ 时, 如答图③, 则 $ ∠AOC = ∠C = 45^{\circ} $;
当 $ AB // OD $ 时, 如答图④, 则 $ ∠BOD = ∠B = 60^{\circ} $,
所以 $ ∠AOC = 360^{\circ} - 90^{\circ} - 90^{\circ} - ∠BOD = 120^{\circ} $;
当 $ OB // CD $ 时, 如答图⑤, 则 $ ∠BOD = ∠D = 45^{\circ} $,
所以 $ ∠AOC = 360^{\circ} - 90^{\circ} - 90^{\circ} - ∠BOD = 135^{\circ} $.
综上, $ ∠AOC $ 的其余可能的度数为 $ 30^{\circ} $ 或 $ 45^{\circ} $ 或 $ 120^{\circ} $ 或 $ 135^{\circ} $.
27. (1) ① 相等 ② 互补
(2) 解: ① 如答图①, 过点 $ O $ 作 $ OE // AB $,

又因为 $ AB // CD $, 所以 $ AB // CD // OE $,
所以 $ ∠AOE = ∠A = 30^{\circ} $, $ ∠COE = ∠C = 45^{\circ} $,
所以 $ ∠AOC = ∠AOE + ∠COE = 75^{\circ} $.
② 当 $ AB // OC $ 时, 如答图②, 则 $ ∠AOC = ∠A = 30^{\circ} $;
当 $ OA // CD $ 时, 如答图③, 则 $ ∠AOC = ∠C = 45^{\circ} $;
当 $ AB // OD $ 时, 如答图④, 则 $ ∠BOD = ∠B = 60^{\circ} $,
所以 $ ∠AOC = 360^{\circ} - 90^{\circ} - 90^{\circ} - ∠BOD = 120^{\circ} $;
当 $ OB // CD $ 时, 如答图⑤, 则 $ ∠BOD = ∠D = 45^{\circ} $,
所以 $ ∠AOC = 360^{\circ} - 90^{\circ} - 90^{\circ} - ∠BOD = 135^{\circ} $.
综上, $ ∠AOC $ 的其余可能的度数为 $ 30^{\circ} $ 或 $ 45^{\circ} $ 或 $ 120^{\circ} $ 或 $ 135^{\circ} $.