21. (10 分)先化简,再求值:$(x - 1)^{2}-2x(x - 3)+(x + 2)(x - 2)$,其中$x = -\dfrac{1}{4}$.
答案:21. 解: 原式 $ = x^{2} - 2x + 1 - 2x^{2} + 6x + x^{2} - 4 = 4x - 3 $.
当 $ x = -\frac{1}{4} $ 时,
原式 $ = 4 × (-\frac{1}{4}) - 3 = -4 $.
当 $ x = -\frac{1}{4} $ 时,
原式 $ = 4 × (-\frac{1}{4}) - 3 = -4 $.
22. (10 分)已知关于$x$,$y$的方程组$\begin{cases}2x - 3y = 3 \\ ax + by = 1\end{cases}$和$\begin{cases}3x + 2y = 11 \\ ay - bx = 3\end{cases}$的解相同,求$(2a - b)^{2}$的值.
答案:22. 解: 由方程组 $ \begin{cases} 2x - 3y = 3, \\ 3x + 2y = 11 \end{cases} $ 解得 $ \begin{cases} x = 3, \\ y = 1. \end{cases} $
所以 $ \begin{cases} 3a + b = 1, \\ a - 3b = 3, \end{cases} $ 解得 $ \begin{cases} a = \frac{3}{5}, \\ b = -\frac{4}{5}. \end{cases} $
所以 $ (2a - b)^{2} = [2 × \frac{3}{5} - (-\frac{4}{5})]^{2} = 2^{2} = 4 $.
所以 $ \begin{cases} 3a + b = 1, \\ a - 3b = 3, \end{cases} $ 解得 $ \begin{cases} a = \frac{3}{5}, \\ b = -\frac{4}{5}. \end{cases} $
所以 $ (2a - b)^{2} = [2 × \frac{3}{5} - (-\frac{4}{5})]^{2} = 2^{2} = 4 $.
23. (10 分)为创建绿色校园,学校决定在一块正方形的空地上种植花草,现向学生征集设计图案. 图案要求只能用圆弧在正方形内加以设计,使正方形和所画的圆弧构成图案,种植花草部分用阴影表示. 请你运用平移、旋转、轴对称等知识,在图③,图④,图⑤中画出三种不同的设计图案(温馨提示:在两个图案中,只有半径变化而圆心不变的图案属于同一种,例如:图①,图②只能算一种).
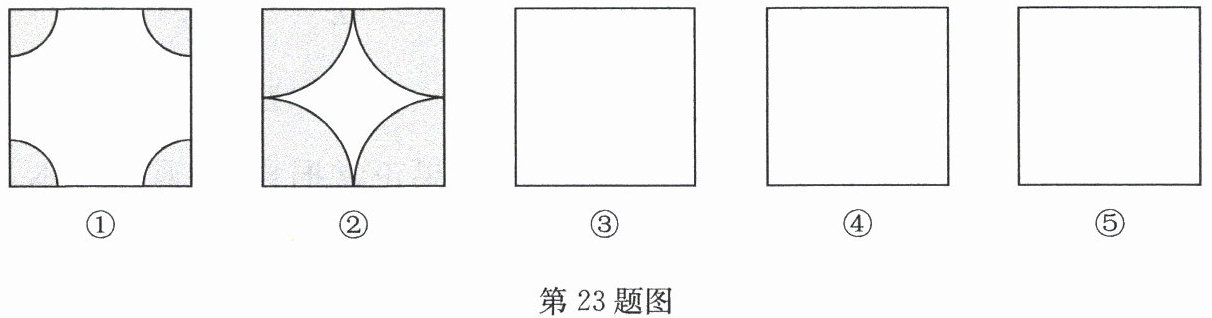

答案:
23. 解: 如答图所示. (答案不唯一)
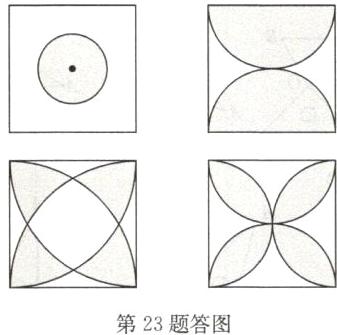
23. 解: 如答图所示. (答案不唯一)

24. (10 分)小明有 1 元和 5 角两种硬币共 12 枚,这些硬币的总币值小于 8 元.
(1) 根据题意,甲、乙两名同学分别列出尚不完整的不等式如下:
甲:$x +$
根据甲、乙两名同学所列的不等式,请你分别指出未知数$x$表示的意义,然后在横线上补全甲、乙两名同学所列的不等式:甲:$x$表示
(2) 求小明可能有几枚 5 角的硬币. (写出完整的解答过程)
(1) 根据题意,甲、乙两名同学分别列出尚不完整的不等式如下:
甲:$x +$
$0.5 × (12 - x)$
$< 8$;乙:$0.5x +$$1 × (12 - x)$
$< 8$.根据甲、乙两名同学所列的不等式,请你分别指出未知数$x$表示的意义,然后在横线上补全甲、乙两名同学所列的不等式:甲:$x$表示
小明有 1 元硬币的枚数
;乙:$x$表示小明有 5 角硬币的枚数
.(2) 求小明可能有几枚 5 角的硬币. (写出完整的解答过程)
答案:24. (1) $ 0.5 × (12 - x) $ $ 1 × (12 - x) $ 小明有 1 元硬币的枚数 小明有 5 角硬币的枚数
(2) 解: 设小明可能有 5 角的硬币 $ x $ 枚, 根据题意, 得 $ 0.5x + 1 × (12 - x) < 8 $, 解得 $ x > 8 $.
因为 $ x $ 是自然数, 且 $ x < 12 $,
所以 $ x $ 可取 9, 10, 11.
答: 小明可能有 5 角的硬币 9 枚, 10 枚, 11 枚.
(2) 解: 设小明可能有 5 角的硬币 $ x $ 枚, 根据题意, 得 $ 0.5x + 1 × (12 - x) < 8 $, 解得 $ x > 8 $.
因为 $ x $ 是自然数, 且 $ x < 12 $,
所以 $ x $ 可取 9, 10, 11.
答: 小明可能有 5 角的硬币 9 枚, 10 枚, 11 枚.
25. (12 分)某校准备组织七年级 400 名学生参加综合实践活动,已知用 1 辆小客车和 2 辆大客车均满载,每次可运送学生 110 名;用 3 辆小客车和 1 辆大客车均满载,每次可运送学生 105 名.
(1) 每辆小客车和每辆大客车各能坐多少名学生?
(2) 若学校计划租用小客车$x$辆,大客车$y$辆,一次运送所有学生,且恰好每辆车都坐满.
①请你设计出所有的租车方案;
②若小客车每辆需租金 1600 元,大客车每辆需租金 2700 元,请选出最省钱的租车方案,并求出最少租金.
(1) 每辆小客车和每辆大客车各能坐多少名学生?
(2) 若学校计划租用小客车$x$辆,大客车$y$辆,一次运送所有学生,且恰好每辆车都坐满.
①请你设计出所有的租车方案;
②若小客车每辆需租金 1600 元,大客车每辆需租金 2700 元,请选出最省钱的租车方案,并求出最少租金.
答案:25. 解: (1) 设每辆小客车和每辆大客车各能坐 $ m $ 名, $ n $ 名学生, 根据题意, 得 $ \begin{cases} m + 2n = 110, \\ 3m + n = 105, \end{cases} $ 解得 $ \begin{cases} m = 20, \\ n = 45. \end{cases} $
答: 每辆小客车和每辆大客车各能坐 20 名和 45 名学生.
(2) ① 由题意, 得 $ 20x + 45y = 400 $, 从而 $ x = 20 - \frac{9}{4}y $.
因为 $ x $, $ y $ 均为自然数,
所以当 $ y = 0 $ 时, $ x = 20 $; 当 $ y = 4 $ 时, $ x = 11 $; 当 $ y = 8 $ 时, $ x = 2 $.
答: 共有 3 种租车方案: 小客车 20 辆, 大客车 0 辆或小客车 11 辆, 大客车 4 辆或小客车 2 辆, 大客车 8 辆.
② 因为小客车每辆需租金 1600 元, 大客车每辆需租金 2700 元,
所以当 $ y = 0 $, $ x = 20 $ 时, 租金为 $ 20 × 1600 = 32000 $ (元);
当 $ y = 4 $, $ x = 11 $ 时, 租金为 $ 11 × 1600 + 4 × 2700 = 28400 $ (元);
当 $ y = 8 $, $ x = 2 $ 时, 租金为 $ 2 × 1600 + 8 × 2700 = 24800 $ (元).
答: 最省钱的租车方案是租小客车 2 辆, 大客车 8 辆, 最少租金为 24800 元.
答: 每辆小客车和每辆大客车各能坐 20 名和 45 名学生.
(2) ① 由题意, 得 $ 20x + 45y = 400 $, 从而 $ x = 20 - \frac{9}{4}y $.
因为 $ x $, $ y $ 均为自然数,
所以当 $ y = 0 $ 时, $ x = 20 $; 当 $ y = 4 $ 时, $ x = 11 $; 当 $ y = 8 $ 时, $ x = 2 $.
答: 共有 3 种租车方案: 小客车 20 辆, 大客车 0 辆或小客车 11 辆, 大客车 4 辆或小客车 2 辆, 大客车 8 辆.
② 因为小客车每辆需租金 1600 元, 大客车每辆需租金 2700 元,
所以当 $ y = 0 $, $ x = 20 $ 时, 租金为 $ 20 × 1600 = 32000 $ (元);
当 $ y = 4 $, $ x = 11 $ 时, 租金为 $ 11 × 1600 + 4 × 2700 = 28400 $ (元);
当 $ y = 8 $, $ x = 2 $ 时, 租金为 $ 2 × 1600 + 8 × 2700 = 24800 $ (元).
答: 最省钱的租车方案是租小客车 2 辆, 大客车 8 辆, 最少租金为 24800 元.