9. 有下列图形:①线段;②角;③长方形;④平行四边形;⑤圆;⑥梯形. 其中是轴对称图形的是
①②③⑤
.(填序号)答案:9. ①②③⑤
10. “同旁内角互补”的逆命题是
互补的两个角是同旁内角
.答案:10. 互补的两个角是同旁内角
11. 一个多边形的每一个外角都等于$18^{\circ}$,则该多边形的内角和等于
$3240^{\circ}$
.答案:11. $3240^{\circ}$
解析:
因为多边形的外角和为$360^{\circ}$,每一个外角都等于$18^{\circ}$,所以该多边形的边数为$360^{\circ}÷18^{\circ}=20$。根据多边形内角和公式$(n - 2)×180^{\circ}$(其中$n$为边数),可得该多边形内角和为$(20 - 2)×180^{\circ}=18×180^{\circ}=3240^{\circ}$。
$3240^{\circ}$
$3240^{\circ}$
12. 如果$(x + 3)(x - 2)=x^{2}+mx + n$,那么代数式$(5m + n)^{2025}$的值为
$-1$
.答案:12. $-1$
解析:
$(x + 3)(x - 2)$
$=x^2 - 2x + 3x - 6$
$=x^2 + x - 6$
因为$(x + 3)(x - 2)=x^2 + mx + n$,所以$m=1$,$n=-6$。
$5m + n=5×1 + (-6)=5 - 6=-1$
则$(5m + n)^{2025}=(-1)^{2025}=-1$
$-1$
$=x^2 - 2x + 3x - 6$
$=x^2 + x - 6$
因为$(x + 3)(x - 2)=x^2 + mx + n$,所以$m=1$,$n=-6$。
$5m + n=5×1 + (-6)=5 - 6=-1$
则$(5m + n)^{2025}=(-1)^{2025}=-1$
$-1$
13. 关于$x$,$y$的二元一次方程$kx + 3y = 5$有一个解是$\begin{cases}x = 2 \\ y = 1\end{cases}$,则$k$的值为 ______ .
答案:13. 1
解析:
将$\begin{cases}x = 2 \\ y = 1\end{cases}$代入方程$kx + 3y = 5$,得$2k + 3×1 = 5$,解得$k = 1$。
1
1
14. 若$a + b = 5$,$a - b = 2$,则$(a + 1)^{2}-(b - 1)^{2}$的值为
20
.答案:14. 20
解析:
$(a + 1)^{2}-(b - 1)^{2}$
$=[(a + 1)+(b - 1)][(a + 1)-(b - 1)]$
$=(a + 1 + b - 1)(a + 1 - b + 1)$
$=(a + b)(a - b + 2)$
因为$a + b = 5$,$a - b = 2$,所以原式$=5×(2 + 2)=5×4=20$
$=[(a + 1)+(b - 1)][(a + 1)-(b - 1)]$
$=(a + 1 + b - 1)(a + 1 - b + 1)$
$=(a + b)(a - b + 2)$
因为$a + b = 5$,$a - b = 2$,所以原式$=5×(2 + 2)=5×4=20$
15. 若关于$x$的不等式$(n + 7)x < n + 7$的解集是$x > 1$,则$n$的取值范围是
$n < -7$
.答案:15. $n < -7$
解析:
解:因为不等式$(n + 7)x < n + 7$的解集是$x > 1$,不等式两边同时除以$n + 7$后不等号方向改变,所以$n + 7 < 0$,解得$n < -7$。
$n < -7$
$n < -7$
16. 某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题. 如图,$AB // CD$,$∠ BAE = 78^{\circ}$,$∠ DCE = 120^{\circ}$,则$∠ E$的度数是
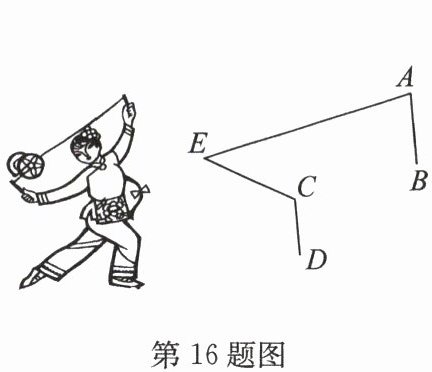
$42^{\circ}$
.
答案:16. $42^{\circ}$
解析:
解:延长DC交AE于点F。
∵AB//CD,
∴∠CFE=∠BAE=78°。
∵∠DCE=120°,∠DCE+∠ECF=180°,
∴∠ECF=180°-120°=60°。
在△ECF中,∠E=180°-∠CFE-∠ECF=180°-78°-60°=42°。
故∠E的度数是$42^{\circ}$。
∵AB//CD,
∴∠CFE=∠BAE=78°。
∵∠DCE=120°,∠DCE+∠ECF=180°,
∴∠ECF=180°-120°=60°。
在△ECF中,∠E=180°-∠CFE-∠ECF=180°-78°-60°=42°。
故∠E的度数是$42^{\circ}$。
17. 苹果的进价是每千克 7.6 元,销售中估计有 5%的苹果正常损耗,为避免亏本,商家把售价应该至少定为每千克
8
元.答案:17. 8
解析:
设商家把售价应该定为每千克$x$元,设苹果的总重量为$m$千克。
因为有$5\%$的苹果正常损耗,所以未损耗的苹果重量为$m(1 - 5\%) = 0.95m$千克。
要避免亏本,则销售未损耗苹果的收入应不低于苹果的进价,可得:
$0.95m · x ≥ 7.6m$
两边同时除以$m$($m > 0$),得:
$0.95x ≥ 7.6$
解得:
$x ≥ \frac{7.6}{0.95} = 8$
所以商家把售价应该至少定为每千克$8$元。
8
因为有$5\%$的苹果正常损耗,所以未损耗的苹果重量为$m(1 - 5\%) = 0.95m$千克。
要避免亏本,则销售未损耗苹果的收入应不低于苹果的进价,可得:
$0.95m · x ≥ 7.6m$
两边同时除以$m$($m > 0$),得:
$0.95x ≥ 7.6$
解得:
$x ≥ \frac{7.6}{0.95} = 8$
所以商家把售价应该至少定为每千克$8$元。
8
18. (2025·宿城区期末)在$△ ABC$中,$∠ A = 65^{\circ}$,将$∠ B$,$∠ C$按照如图所示折叠. 若$∠ ADB' = 35^{\circ}$,则$∠ 1 + ∠ 2 + ∠ 3 =\_\_\_\_\_\_^{\circ}$.
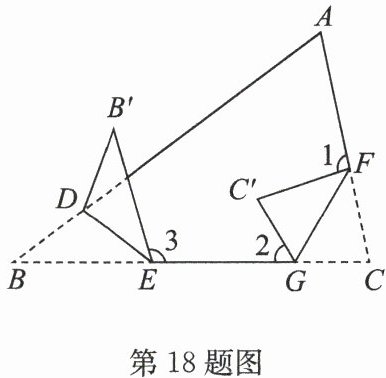

答案:18. 265
解析:
解:在$△ ABC$中,$∠ A=65^{\circ}$,则$∠ B+∠ C=180^{\circ}-65^{\circ}=115^{\circ}$。
由折叠性质,$∠ B=∠ B'$,$∠ C=∠ C'$,$∠ BED=∠ B'ED$,$∠ CGF=∠ C'GF$。
$∠ ADB'=35^{\circ}$,则$∠ BDB'=180^{\circ}-35^{\circ}=145^{\circ}$。
在四边形$DB'EB$中,$∠ B+∠ B'+∠ BDB'+∠ B'EB=360^{\circ}$,即$2∠ B+145^{\circ}+∠ B'EB=360^{\circ}$,得$∠ B'EB=215^{\circ}-2∠ B$,故$∠ 3=180^{\circ}-∠ B'EB=2∠ B-35^{\circ}$。
同理,$∠ 2=2∠ C-35^{\circ}$。
$∠ 1=180^{\circ}-∠ ADB'=145^{\circ}$。
$∠ 1+∠ 2+∠ 3=145^{\circ}+(2∠ C-35^{\circ})+(2∠ B-35^{\circ})=145^{\circ}-70^{\circ}+2(∠ B+∠ C)=75^{\circ}+2×115^{\circ}=265^{\circ}$。
265
由折叠性质,$∠ B=∠ B'$,$∠ C=∠ C'$,$∠ BED=∠ B'ED$,$∠ CGF=∠ C'GF$。
$∠ ADB'=35^{\circ}$,则$∠ BDB'=180^{\circ}-35^{\circ}=145^{\circ}$。
在四边形$DB'EB$中,$∠ B+∠ B'+∠ BDB'+∠ B'EB=360^{\circ}$,即$2∠ B+145^{\circ}+∠ B'EB=360^{\circ}$,得$∠ B'EB=215^{\circ}-2∠ B$,故$∠ 3=180^{\circ}-∠ B'EB=2∠ B-35^{\circ}$。
同理,$∠ 2=2∠ C-35^{\circ}$。
$∠ 1=180^{\circ}-∠ ADB'=145^{\circ}$。
$∠ 1+∠ 2+∠ 3=145^{\circ}+(2∠ C-35^{\circ})+(2∠ B-35^{\circ})=145^{\circ}-70^{\circ}+2(∠ B+∠ C)=75^{\circ}+2×115^{\circ}=265^{\circ}$。
265
19. (10 分)解方程组:
(1) $\begin{cases}2x + y = 5 \\ 2x - y = 3\end{cases}$
(2) $\begin{cases}2x - 7y = 5 \\ 3x - 8y = 10\end{cases}$
(1) $\begin{cases}2x + y = 5 \\ 2x - y = 3\end{cases}$
(2) $\begin{cases}2x - 7y = 5 \\ 3x - 8y = 10\end{cases}$
答案:19. 解: (1) $ \begin{cases} 2x + y = 5, ① \\ 2x - y = 3, ② \end{cases} $
① + ②, 得 $ 4x = 8 $, $ x = 2 $.
把 $ x = 2 $ 代入①, 得 $ 4 + y = 5 $, $ y = 1 $.
所以原方程组的解为 $ \begin{cases} x = 2, \\ y = 1. \end{cases} $
(2) $ \begin{cases} 2x - 7y = 5, ① \\ 3x - 8y = 10, ② \end{cases} $
① × 3 - ② × 2, 得 $ -5y = -5 $, $ y = 1 $.
把 $ y = 1 $ 代入①, 得 $ 2x - 7 = 5 $, $ x = 6 $.
所以原方程组的解为 $ \begin{cases} x = 6, \\ y = 1. \end{cases} $
① + ②, 得 $ 4x = 8 $, $ x = 2 $.
把 $ x = 2 $ 代入①, 得 $ 4 + y = 5 $, $ y = 1 $.
所以原方程组的解为 $ \begin{cases} x = 2, \\ y = 1. \end{cases} $
(2) $ \begin{cases} 2x - 7y = 5, ① \\ 3x - 8y = 10, ② \end{cases} $
① × 3 - ② × 2, 得 $ -5y = -5 $, $ y = 1 $.
把 $ y = 1 $ 代入①, 得 $ 2x - 7 = 5 $, $ x = 6 $.
所以原方程组的解为 $ \begin{cases} x = 6, \\ y = 1. \end{cases} $
20. (10 分)解不等式$1 - \dfrac{2x + 1}{3} > \dfrac{x + 6}{2}$,并把它的解集在数轴上表示出来.
答案:
20. 解: 去分母, 得 $ 6 - 2(2x + 1) > 3(x + 6) $,
去括号, 得 $ 6 - 4x - 2 > 3x + 18 $,
移项, 得 $ -4x - 3x > 18 - 6 + 2 $,
合并同类项, 得 $ -7x > 14 $,
两边都除以 -7, 得 $ x < -2 $.
所以该不等式的解集为 $ x < -2 $, 在数轴上表示如答图.

20. 解: 去分母, 得 $ 6 - 2(2x + 1) > 3(x + 6) $,
去括号, 得 $ 6 - 4x - 2 > 3x + 18 $,
移项, 得 $ -4x - 3x > 18 - 6 + 2 $,
合并同类项, 得 $ -7x > 14 $,
两边都除以 -7, 得 $ x < -2 $.
所以该不等式的解集为 $ x < -2 $, 在数轴上表示如答图.
